基于虚拟视图和低秩矩阵恢复的视点间预测
刘如意
(北京工业大学计算机学院,北京 100124)
0 引言
多视点视频是由处于空间不同位置的相机阵列拍摄同一场景时得到的一组视频序列信号,能提供拍摄场景不同角度的视频信息,利用其中的一个或多个视点信息可以合成任意视点的信息,达到自由视点显示的目的[1]。视点之间相机位置不同,但存在很强的相关性,即各视点间存在冗余。因此相比于传统的视频编解码,多视点视频编码增加了视点间预测的方式。JMVC采取视差估计的方法,到相邻视图中寻找相似块作为预测值。该方法能够很好地利用视点间信息的冗余,达到了很好的预测效果。但这种方法并没有考虑多视点视频视点间由于相机位置导致的遮挡和形变[2],所以对有遮挡和形变的区域预测效果不是很好。
为了进一步提高视点间预测的效率,本文提出基于虚拟视图和低秩矩阵恢复的视点间预测方法。该方法充分利用了新一代多视点视频格式中的深度图,根据相机内部参数、相机位置参数,利用相邻视图可以合成当前视图的虚拟视图,这就相当于考虑了由于相机位置导致的形变。当有两个或多个虚拟视图的时候,不同虚拟视图被遮挡的部分不同,就能相互补充,这样就可以解决相机位置导致的遮挡问题,所以能够更好地利用视点间的相关性、降低视点间的冗余。并且利用低秩矩阵恢复的方法来对得到的若干个相似块进行恢复处理,以降低噪声信号,得到更好的预测结果。
1 JMVC框架及视点间预测
JMVC是多视点视频编解码MVC的参考软件,由联合视频小组JVT(Joint Video Team)负责实现和改进更新[3]。
多视点视频依然具有传统视频的特性,所以仍然能够进行传统的帧内、帧间预测。但由于多视点视频视点间的冗余,JMVC中使用了分等级的B帧预测结构,如图1所示。
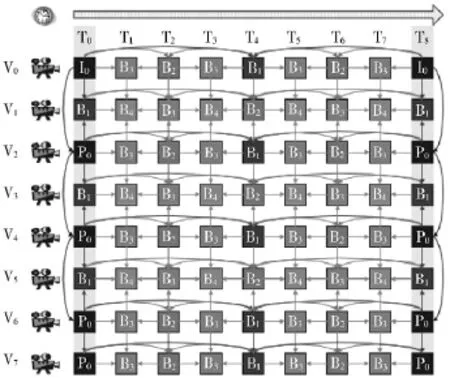
图1 分等级的B帧预测结构
分等级的B帧预测结构将所有视图分成两类,其中 V0、V2、V4、V6称为主视图,V1、V3、V5、V7称为辅视图。主视图只进行运动估计,而当主视图编码完成后,辅视图除了可以进行运动估计外,还可以利用主视图做视差估计,即进行视点间的预测。
JMVC提供了7种大小的块:16×16、16×8、8×16、8×8、8×4、4×8和4×4,供运动估计和视差估计使用[3]。对于辅视图,编码过程中尝试所有大小的块的帧内、帧间、视点间预测方法,然后根据率失真优化模型RDO(Rate-Distortion Optimization)来选择最优的编码模式。这种方法充分利用了同一视图的空间、时间以及不同视图间的信息冗余,所以能够取得很好的压缩效果。
2 基于虚拟视图的预测
2.1 虚拟视图的合成原理
当用摄像机拍摄现实世界中的场景时,得到的图像上的任意点都可以对应到现实场景的一个点,深度图是摄像机到现实场景中点的距离的量化表示。所以根据图像上的点的颜色和深度、摄像机的内部参数、摄像机在现实场景中的位置信息,可以把图像上每一个点重新映射到现实世界中去[4]。
用上述过程的逆过程,可以将现实世界中的点根据机内部参数和位置重新映射到一幅图像上来。由上面两点,可以将一个相机拍摄的图像,经过图像到现实世界,再由现实世界到图像的映射,映射成另一个位置的相机拍摄的图像,即得到虚拟视图。
相机拍摄的图像上每个点的坐标信息用摄像机坐标系表示。摄像机坐标系以摄像机的光心为原点,Xc轴和Yc轴与图像 x、y方向平行,Zc轴为摄像机的光轴,与图像平面垂直[5]。
由于摄像机可以安放在环境中的任何位置,在环境中选定一个基准坐标系来描述相机的位置,并用它描述环境中任何物体的位置,该坐标系称为世界坐标系[5]。
摄像机坐标系与世界坐标系之间的关系可用旋转矩阵R与平移向量t来描述[6]。因此空间中某一点P在世界坐标系与摄像机坐标系下的坐标如果分别为(Xw,Yw,Zw)和(Xc,Yc,Zc),则存在如下关系:
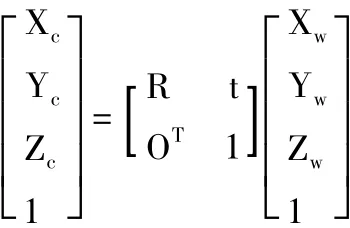
其中,R为3×3正交单位矩阵,t为三维平移向量。
世界坐标中任何点P在图像上的投影p为光心与P点的连线OP与图像平面的交点,称为中心摄影[7]。则以毫米为单位的图像坐标(x,y)与摄像机坐标间的关系可为:
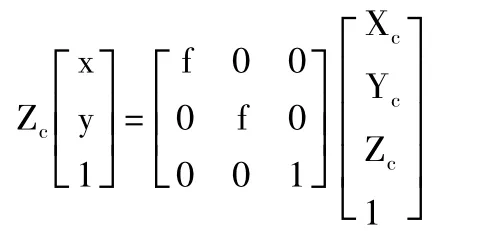
其中f表示摄像机的焦距。
而图像上的坐标一般用像素为单位,这就需要一个物理尺寸坐标到像素坐标的转换:
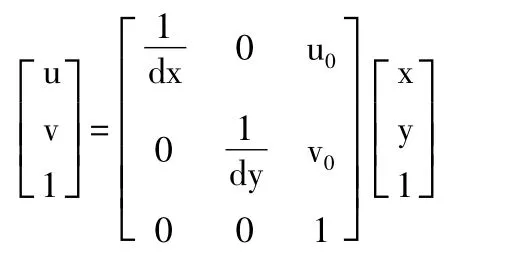
其中,dx、dy为每个像素在 x、y轴上的物理尺寸,O1(u0,v0)为摄像机光轴与图像平面的交点[8]
于是,现实场景中任一点P在图像上以像素为单位的坐标p(u,v)可表示为:

同理,也可以得到以像素为单位的图像坐标到世界坐标的变换。
所以知道另一个相机相对于世界坐标系的旋转矩阵R和平移矩阵t,就能将一个相机拍摄的图像变换到另一个位置的相机拍摄的图像。当然,由于一个位置能看到的场景,由于前景的遮挡,在另一个位置可能看不到,所以会形成一些空洞。但当有两个和两个以上的虚拟视图时,由于相机位置不同,被遮挡的部分也不会相同,相互补充,可以有效地消除空洞。
2.2 利用虚拟视图寻找相似块
如图2所示,可以利用相邻视图生成当前编码视图的虚拟视图。当要编码一个块时,到两边的虚拟视图中找到对应的块,利用两个虚拟视图的块数据合成一个块,作为参考块;然后到相邻视图中寻找若干个与参考块最匹配的块;最后将参考块和符合阈值的若干相似块按列放到一个矩阵中,使用矩阵恢复进行处理,以降低噪声,得到更好的预测结果。

图2 利用虚拟视图进行预测
3 低秩矩阵恢复去噪
3.1 低秩矩阵恢复
低秩矩阵恢复最早由John Wright等人提出,又称为Robust PCA(Principal Component Analysis)或者稀疏与低秩矩阵分解[12]。可以从PCA的角度看这个问题,传统的PCA可以理解为高维数据在低维线性子空间上的投影,它可以写成[12]:

其中,D的每一列均为给定的数据,‖·‖F是矩阵的Frobenius范数,即所有元素的平方和再开根号。
通过此约束优化问题可以找到D在一个最近的r维线性子空间上的投影[13]。当E为轻微的高斯随机噪声时,PCA可以通过一次SVD(Singular Value Decomposition)准确地找到最优的A。但当A被严重破坏,即E很大时,A的估计往往不准确,并且PCA还有一个问题是需要预知子空间维数r。于是提出了Robust PCA来解决A中数据被破坏的情况[14]。
当矩阵的某些元素被严重破坏后,低秩矩阵恢复能够自动识别出被破坏的元素,恢复出原矩阵[11]。当然这需要假定原矩阵有非常好的结构,即低秩的,另外假定只有很少一部分元素被严重破坏,即噪声是稀疏的,但大小可以任意[15]。于是矩阵恢复可以用如下最优化问题描述:
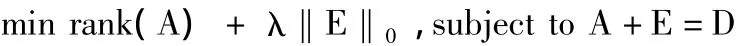
其中,目标函数为矩阵A的秩以及噪声矩阵E的零范数,即E的非零元素的个数;λ表明噪声所占的权重。
利用矩阵的核范数近似秩,矩阵的1范数近似零范数,可将上面的最优化问题转化为如下的问题:
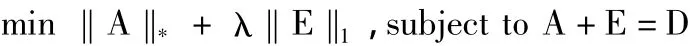
这是一个凸优化问题,可以有效地求解。
3.2 利用低秩矩阵恢复进行去噪处理
矩阵恢复在图像处理中应用广泛,如John Wright等人展示了如何在背景建模、人脸识别等问题中,利用矩阵恢复。Yigang Peng等人将矩阵恢复技术应用于图片对齐中[16]。
本文中,将矩阵恢复应用于对前面得到的相似块进行去噪处理。

图3 利用低秩矩阵进行去噪处理
找到的用于预测的相似块的值都很相近,当把每个块的数据看作一列,放到一个矩阵中去时,它们满足低秩的要求;同时每个相似块中难免存在一些噪声数据(如图3所示),这些噪声数据会对最终的预测结果造成不好的影响。首先,用一个阈值来筛选得到相似块,对于满足条件的块,用低秩矩阵恢复的方法,对这若干个相似块对参考块进行恢复,以降低参考块中的噪声信号,得到更精确的预测值。
4 实验结果
为了验证上述方案的有效性,本文在JMVC框架上进行了验证。首先,替换掉JMVC中一种不常用的模式,来实现该方法;然后对常见的多视点视频序列进行试验,并与JMVC原始的算法进行比较。视频编码中一般用比特率Bitrate衡量压缩大小,用峰值信噪比PSNR(Peak Signal to Noise Ratio)衡量压缩质量。本文综合采用Bitrate和PSNR来进行结果的比较,即比较相同PSNR下的码率。
表1~表3 为 champagne_tower、baloon、kendo三个测试序列的实验结果,其中Bitrate1和PSNR1为JMVC原始结果,Bitrate2和PSNR2为本文提出的方法的结果。

表1 champagne_tower序列结果

表2 baloon序列结果

表3 kendo序列结果
如表1~表3所示,综合考虑4个QP,上述3个常用视频序列在相同的PSNR下,本文提出的方法比JMVC原始方法节省码率分别为 1.484538%、2.191085%、1.005343%。
综上所述,本文的方法在视点间预测的效率上比JMVC原始方法大约节省1% ~2%的码率。
5 结束语
针对多视点视频编码中的视点间预测问题,本文提出一种基于虚拟视图合成和低秩矩阵恢复的预测方法。该方法利用新的多视点视图中的深度图,结合相机的内外参数,并使用计算几何的一些方法,充分利用多视点视频的可用信息,有效地提高了编码压缩的效率,达到了较好的实验效果。实验结果表明,该方法有效地提高了bit-rate,比JMVC原始结果大约节省1%~2%的码率。
[1]JVT-X064,MVC:Experiments on Coding of Multi-view Video Plus Depth[S].
[2]Masayuki Tanimoto,Memno Wildeboer.Framework for FTV coding[C]//Proceedings of the 27th Conference on Picture Coding Symposium.2008:429-432.
[3]Chen Y,Wang Ye-Kui,Ugur K,et al.The emerging MVC standard for 3D video services[J].EURASIP Journal on Advances in Signal Processing,2009,13(1):128-132.
[4]Muller K,Dix K,Kauff P.Reliability-based generation and view synthesis in layered depth video[C]//IEEE 10th Workshop on Multimedia Signal Processing.2008:34-39.
[5]Fehn C.Depth-image-based rendering(DIBR),compression and transmission for a new approach on 3D-TV[C]//Proceedings of the SPIE.2004,5291:93-104.
[6]Kazuo Sugimoto,Mitsuru Kobayashi,Yoshinori Suzuki,et al.Inter frame coding with template matching spatio-temporal prediction[C]//IEEE International Conference on Image Processing.2004:465-468.
[7]Kobayashi M,Suzuki Y,Boon C S,et al.Reduction of information with motion prediction using template matching[C]//Proc.20th Picture Coding Symposium of Japan.2005:17-18.
[8]Zhu C,Lin X,Chau L P.Hexagon-based search pattern for fast block motion estimation[J].IEEE Transactions on Circuits and Systems for Video Technology,2002,12(5):349-355.
[9]Tsung P-K,Yang H-J,Lin P-C,et al.Hybrid color compensation for virtual view synthesis in multiview video applications[C]//Proceedings of 2010 IEEE International Symposium on Circuits and Systems.2010:121-124.
[10]Fan Y C,Wu S F,Lin B L.Three-dimensional depth map motion estimation and compensation for 3D video compression[J].IEEE Transactions on Magnetics,2011,47(3):691-695.
[11]Scharstein D,Szeliski R.A taxonomy and evaluation of dense two-frame stereo correspondence algorithm[J].Intl.Journal of Computer Vision,2002,47(1):7-42.
[12]Suzuki Y,Boon C S,Kato S.Block-based reduced resolution inter frame coding with template matching prediction[C]//IEEE International Conference on Image Processing.2006:1701-1704.
[13]Singer A,Cucuringu M.Uniqueness of low-rank matrix completion by rigidity Theory[J].SIAM Journal on Matrix Analysis and Applications,2010,31(4):1621-1641.
[14]Peng Y,Ganesh A,Wright J,et al.RASL:Robust alignment by sparse and low-rank decomposition for linearly correlated images[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition.2010:763-770.
[15]Zhou B B,Brent R P.A parallel ring ordering algorithm for efficient one-sided Jacobi SVD computations[J].Journal of Parallel and Distributed Computing,1997,42(1):1-10.
[16]Abernethy J,Bach F,Evgeniou T,et al.Low-rank matrix factorization with attributes[J].Computing Research Repository,2006.

