考虑支座效应的石英晶体谐振器研究

吴荣兴，李继亮，于兰珍，王 骥

(1.宁波职业技术学院建筑工程系，浙江 宁波 315800;2.宁波大学机械工程与力学学院，浙江 宁波 315211)

0 引言

石英晶体谐振器的振动规律可以由三维运动方程加上边界条件进行精确描述，但异常复杂的运动方程和边界条件使得几乎不可能求得解析解［1-5］。利用有限元法求解此类问题时，庞大的矩阵运算需要极长的计算时间和极大的内存存储量，而且求得结果后处理也非常复杂，因此在实际应用方面受到束缚［6-8］。随后开发的专用软件在三维理论中考虑压电强化，可以消去电场而简化为纯粹的机械振动问题;同时采用Mindlin板理论，可以使有限元计算的自由度减少，并且计算结果也比较精确［9-14］。实际产品中石英晶体板是通过导电胶体固定在封装基座上，研究发现导电胶体支座同样会对剪切振动的频率和振动模态有很大的影响［15］。本文分析考虑不同因素情况下导电胶支座对石英晶体谐振器振动频率和振动模态的影响。

1 板长对厚度剪切振动频率的影响

为了利用有限元软件进行模拟，在石英晶体板模型上添加导电胶体支座，其基本模型如图1所示。为了更好地模拟实际产品，设定模型中导电胶是由与右侧面接触的半圆柱体和与上下两个表面接触的半球体组成。该模型中导电胶支座始终与石英晶体板粘接一起，且半圆柱底面受3个方向上的位移约束［16-17］。在计算中，为了能够与不添加支座下自由振动的频率相比较，同时不破坏在无支座下自由振动时对矩形石英晶体板的网格的划分，放弃了利用GLUE命令将导电胶与石英晶体板直接粘接，然后划分网格的办法而采用ANSYS中的接触分析相关指令，将接触条件设定为导电胶支座与石英晶体板接触面始终保持面面接触不分离［16-17］。在给导电胶支座半圆球面添加Ux、Uy、Uz方向上的位移约束后，便可利用ANSYS模态分析模块进行厚度剪切振动模态分析。导电胶支座为各向同性材料，其弹性模量为192.8MPa，泊松比为 0.3，采用 SOLID98 耦合场四面体单元对其进行模拟，同时对其进行自由网格划分;石英晶体板仍用SOLID226耦合场六面体单元进行模拟。得到的有限元模型如图1所示。

图1 石英晶体板模型

在考虑添加支座后石英晶体板的长度对频率影响的有限元计算中，设定导电胶支座的半径大小不变，其值为100μm。两个导电胶支座对称于X轴，距离前后表面为1/2 c(2c为石英晶体板的宽度)，支座间距为c。

为了与无支座自由振动的石英晶体板自由振动的频率进行比较，在有限元模拟中同样每隔0.1b长度便计算一次厚度剪切振动的频率。当石英晶体板的长度增加2b以上沿长度方向上划分的网格数量为110。在获得添加支座后的石英晶体板长度的变化对频率的影响曲线后，进一步将其与自由振动时石英晶体板的长度变化对频率的影响相比较，得到两者之间的频率变化曲线图如图2所示。

图2 添加支座和自由振动板长变化对厚度剪切振动频率的影响曲线

2 点胶半径对厚度剪切振动频率的影响

在石英晶体板的封装过程中，与石英晶体板相接触的导电胶支座半径的大小同样也会对谐振器的频率造成影响。为此，本文设初始点胶半径R大小为120μm，并且点胶位置距离前后表面各为1/2c，两个点胶之间的距离为c，石英晶体板的长宽高各为2a、2c、2b，如图1所示。在每次分析过程中不改变点胶的位置，仅改变半径的大小来观察点胶半径变化对厚度剪切振动频率的影响，模态分析约束的添加以及其他条件与前面的分析相同。每次计算过程中点胶的半径每次按照初始半径的1/16递减，即每1/16 R计算一次。最终获得点胶半径变化对频率的影响曲线如图3所示。

图3 点胶半径变化对厚度剪切振动频率的影响

从图3中可以发现，随点胶半径的增加，石英晶体谐振器的频率是逐渐增加的。但是这种改变并不是特别明显，尽管半径大小改变跨越很大，厚度剪切振动频率的改变仅在3个ppm(百万分之一)之间。图3中直线是计算结果进行数据拟合的结果。由于石英晶体板本身尺寸就很小，固定的难度当然就很大，该计算结果表明在设计时没有必要刻意使得导电点胶的半径很小，半径对厚度剪切振动频率的影响相对于板的长度和宽度尺寸的改变并不是特别明显。

3 支座间距对厚度剪切振动频率的影响

在封装过程中，影响石英晶体板厚度剪切振动频率的另一个重要因素是两个导电胶支座之间的距离［15］。在讨论导电胶支座间距对石英晶体板厚度剪切振动频率的影响中，本文设定导电胶支座半径大小为100μm，石英晶体板长宽高尺寸同样为2a、2c、2b。两个支座对称于Z轴，距前后表面距离相等。为了研究导电胶距离变化对其影响，让支座间距从4/8c变化到14/8 c(支座间距小于4/8 c时两个支座会相接触，大于14/8 c时就基本脱离石英板)，观察其对厚度剪切振动频率的影响，如图4所示。

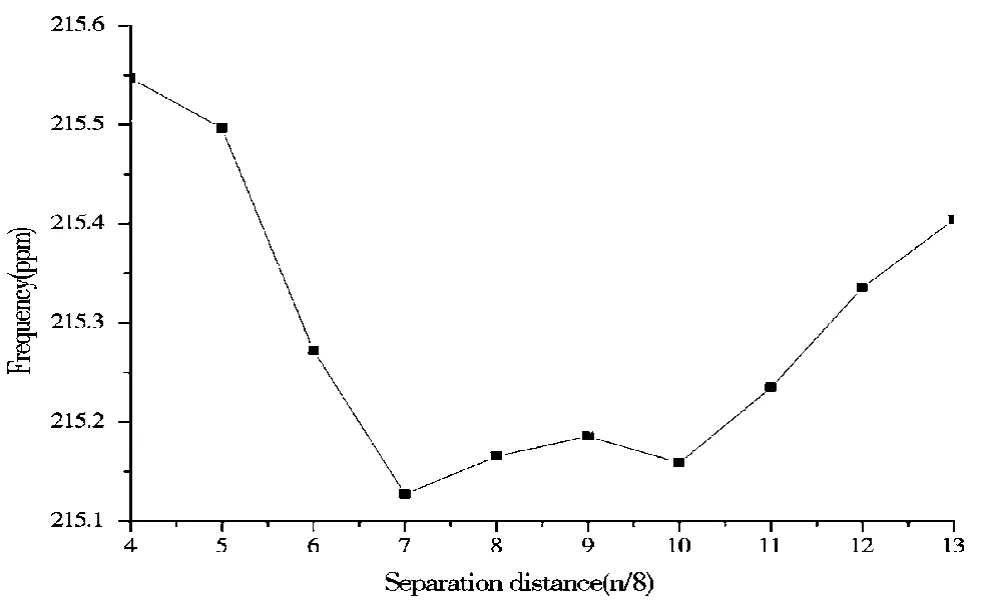
图4 点胶半径变化对厚度剪切振动频率的影响

从图4中发现并不是按照所想象的那样，随导电胶支座间距的增大厚度剪切振动频率会逐渐减小。在支座间距为7/8c到10/8c之间的变化较为平缓，在其他数值处的跳动比较大。这也说明了导电胶支座间距会对厚度剪切振动频率带来影响。但是如与点胶半径那样，导电胶支座间距对石英晶体板的厚度剪切振动频率的影响是非常小的。从图4中可以看出在两个导电胶支座间距由近到远的过程中，仅仅只改变0.5个ppm。同时，在这一变化过程中，始终能够得到十分清晰的厚度剪切振动位移云图。图5为两支座间距为14/8c时的厚度剪切振动位移云图(两个导电胶支座十分靠外)。

图5 支座间距为14/8c时石英晶体板厚度剪切振动位移云图

最后，本文比较了支座间距为4/8c、10/8c与14/8c时的Ux位移沿X方向上的位移分布如图6所示，发现基本上是重合的。如同点胶半径大小那样，导电胶支座间距的变化对厚度剪切振动频率并不是特别明显，因此在设计中没有必要刻意通过改变两个点胶的相对位置来改变厚度剪切振动频率，但是建议最好处在中间位置附近较佳。

图6 不同支座间距下Ux位移沿X方向的分布

4 结束语

本文在添加点胶的有限元模型基础上，通过改变石英晶体板的长度尺寸以及点胶半径和支座间距，得到了板长、点胶半径和支座间距对厚度剪切振动频率的影响曲线图，并详细分析了在添加导电胶支座后石英晶体板的长度变化和自由振动时石英晶体板的长度变化的异同，这将在今后该方面的解析解和产品的设计中起到作用。

［1］Yang J S.An Introduction to the Theory of Piezoelectricity［M］.Berlin，Springer，2005.

［2］Yang J S.The Mechanics of Piezoelectric Structures［M］.Singapore，World Scientific，2006.

［3］Yang J S.Analysis of Piezoelectric Devices［M］.Singapore，World Scientific，2006.

［4］李允，沈星，王宁.压电陶瓷驱动器性能的理论计算与ANSYS仿真［J］.安徽工业大学学报:自然科学版，2008，25(4):394-398.

［5］陈晟，杨俊.基于ANSYS的压电圆片振子径向振动模式分析［J］.计算机仿真，2009，26(3):318-321.

［6］雷辉，周双娥.用ANSYS软件分析压电陶瓷的振动状态［J］.湖北大学学报:自然科学版，2008，30(1):29-33.

［7］张涛，孙立宁，蔡鹤皋.压电陶瓷基本特性研究［J］.光学精密工程，1998，6(5):26-32.

［8］林书玉.压电陶瓷薄圆环振子径向振动的机电等效电路及其分析［J］.应用声学，2005，24(3):140-146.

［9］陈洋洋.考虑复杂因素的石英晶体谐振器并行有限元分析［D］.宁波:宁波大学，2012.

［10］史俊.复杂结构的有限元计算［D］.宁波:宁波大学，2010.

［11］Wang J，Yu J D，Yong Y-K，et al.A finite element analysis of frequency-temperature relations of AT-cut quartz crystal resonators with higher-order Mindlin plate theory［J］.Acta Mechanica，2008，199(1-4):117-130.

［12］Wang J，Zhao W H.The determination of the optimal length of crystal blanks in quartz crystal resonators［J］.IEEE Transactions on Ultrasonics，Ferroelectrics and Frequency Control，2005，52(11):2023-2030.

［13］Wang J，Zhao W H，DU J K，et al.The calculation of electrical parameters of AT-cut quartz crystal resonators with the consideration of material viscosity［J］.Ultrasonics，2011，51(1):65-70.

［14］Wang J，Yang L J，Pan Q Q，et al.Resonant frequency function of thickness-shear vibrations of rectangular crystal plates［J］.IEEE Transactions on Ultrasonics，Ferroelectrics and Frequency Control，2011，58(5):1102-1107.

［15］冯冠平.谐振传感理论及器件［M］.北京:清华大学出版社，2008.

［16］龚曙光，谢桂兰，黄云清.ANSYS参数化编程与命令手册［M］.北京:机械工业出版社，2009.

［17］张倩，胡仁喜，康士廷.ANSYS12.0电磁学有限元分析从入门到精通［M］.北京:机械工业出版社，2010.