基于断裂理论的大体积混凝土裂缝分析

李彩华，肖盛燮，高路恒

（重庆交通大学，重庆 400074）

1 大体积混凝土温度裂缝产生机理

1.1 混凝土温度变化分析

对于大型的混凝土结构来说，施工一般采用分层、分段浇筑，施工浇筑过程中，对最底层的混凝土中心温度变化进行分析（见图1、图2）。

在大型混凝土（如混凝土堤坝）施工时，其温度从最高降到稳定温度需要的时间较长，有的甚至需要几十年，所以，需要人工降温。

1.2 混凝土温度应力及裂缝分析

如图2所示，混凝土的弹性模量及强度随时间逐渐增加，应力发展可根据温度的变化分为3个阶段：

第一阶段，混凝土中的水泥放热基本完成，这个过程一般需要一个月，混凝土中会产生大量的水化热，弹性模量急剧变化。

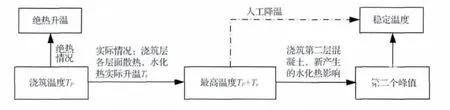
图1 混凝土浇筑温变流程

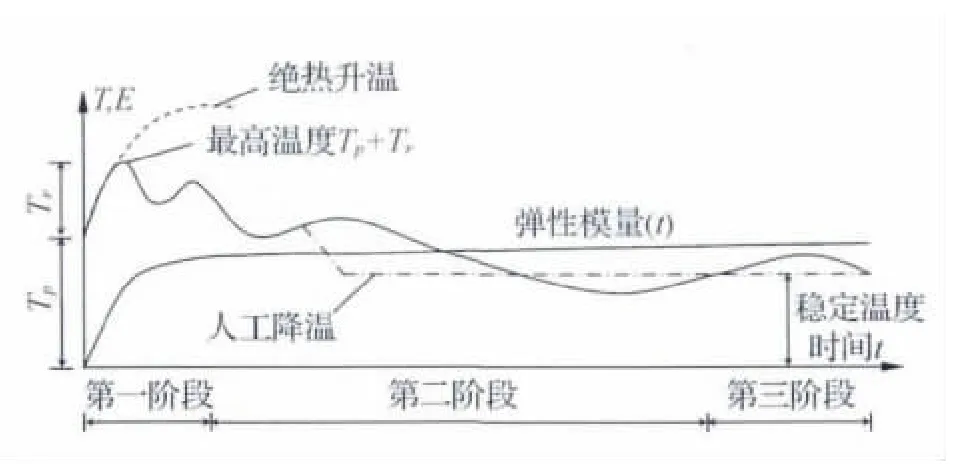
图2 混凝土温度以及弹性模量随时间的变化

第二阶段，水化热释放基本完成到混凝土达到稳定的温度，此过程是混凝土内外温差产生温度应力，弹性模量变化幅度较小。

第三阶段，混凝土温度基本稳定，温度应力主要由外界温度变化引起。

在大体积混凝土结构中一般水泥用量较多，截面尺寸大，水泥产生水化热较多，混凝土养护前期，表面升温的同时会释放一部分热量，整个结构由内到外，而温度由高到底，形成不同的温度层。根据热胀冷缩的原理，中心部位高于表面温度，膨胀速度相对表面较快，表面约束中心，内部受压，表面受拉，当混凝土表面拉应力大于混凝土抗拉强度时，就会出现表面裂缝，这主要体现在第一阶段。当水化热作用完成时，混凝土降温逐渐下降，混凝土在原有的膨胀基础上产生收缩，表面与中心温度仍然存在较大差值，收缩速度不同，此过程是中心约束表面，一般还会有基础或者支座的约束，内部收缩产生拉应力，产生的拉应力超过膨胀的压应力时，会产生贯穿裂缝。

2 大体积混凝土的断裂韧度

大体积混凝土施工阶段的裂纹多由拉应力产生，属于裂纹扩展类型中的第一种（见图3）——张开型。坐标系如图4所示，根据弹性力学分析，裂纹尖端附近的应力分量和位移分量可表示为

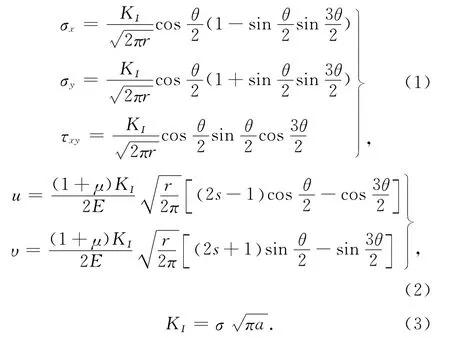
式中：（γ，θ）为以裂纹顶点为原点的极坐标，KΙ为Ⅰ型应力强度因子，σ为断裂应力，a为裂纹长度的一半，Ε为弹性模量，μ为泊松比。

裂纹尖端的扩展与应力强度因子KΙ是否达到临界值KΙc有关，裂纹扩展的临界条件可写为KΙ＝KΙc。当KΙ达到KΙc时，裂纹将扩展；而当KΙ＜KΙc时，裂纹不扩展。KΙc是通过材料试验测定的，表征材料对裂纹扩展的抗力，称为断裂韧度。经过大量试验统计分析，于晓中等建议用下式估算混凝土的断裂韧度

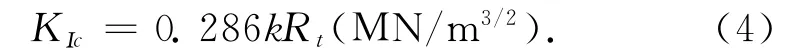
其中，对于大体积混凝土取k＝1.9，混凝土劈裂抗拉强度Rt的量纲为MPa，即

由上可知裂纹尖端应力值σ与混凝土劈裂抗拉强度Rt的关系

3 施工期微裂纹发展规律

3.1 温度控制因素

混凝土的浇筑温度和水化热升温是控制大体积混凝土微裂纹发展的主要因素。从温度控制观点来看主要涉及3个特征温度：①混凝土浇筑温度TP，混凝土建筑物的起始温度；②混凝土最高温度TP＋Tr，等于浇筑温度TP加水化热升温Tr；③最终温度Tf。

混凝土强度是通过水泥不断水化体现的，水泥水化越充分整个混凝土结构强度越接近于设计强度值。然而，水泥水化反应为放热反应，过高的温度不利于混凝土强度发展。大体积混凝土结构断面尺寸比较大，内部水化热不易散失，与表面环境温度形成较大温差，抑制混凝土强度的发展。因此，TP＋Tr与外界温度T0之差△T是控制施工期裂纹发展的关键，为防止温差过大需采取保温隔热措施。

保温隔热措施可以有效的降低△T，阻止裂纹的发生。下面以寒潮期间混凝土坝体为例，说明表面保温λ／β对混凝土表面降温幅度的影响：

按无限大平板计算，厚度为2R。寒潮期间气温变化用折线近似表示为

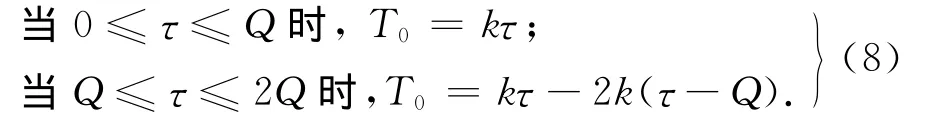
温度场的初始条件和边界条件为

满足这些条件和热传导方程的解为

在表面上温度最低、应力最大，式（10）中令x＝R，表面温度为

式中：λ为导热系数，a为导温系数，μn为特征方程的根，β为表面放热系数。

由式（10）计算的温度见图5，可以看出表面保温λ／β对混凝土表面降温幅度的影响十分显著。

表面保温系数λ／β可以有效降低混凝土表面降温幅度。λ／β越大，降温效果越明显；对于相同的保温系数λ／β，随着养护时间的增长，混凝土表面降温幅度增大。因此，浇筑大体积混凝土早期必须加强保温措施，使内外温差均衡下降。

图5 寒潮期间混凝土表面最低温度

3.2 裂纹尖端应力值折减

混凝土养护龄期内，实际的混凝土劈裂抗拉强度远比设计抗拉强度Rt低。根据公式（5）知，实际的断裂韧度也较小，由公式（6）可得

由上式知，混凝土劈裂抗拉强度Rt与裂纹尖端应力值σ成正比。施工阶段由于混凝土内外温差，减缓了混凝土劈裂抗拉强度Rt的增长，则裂纹尖端应力值σ也较小，出现裂纹尖端应力值的折减。

4 结 论

1）把混凝土龄期分为三个阶段来分析其内部应力变化，以及引起的混凝土开裂机制。

2）施工阶段大体积混凝土裂纹尖端临界应力强度因子KΙc较小，实际施工中容易达到，提供了微裂纹生成的外部条件。

3）采取保温措施可以有效降低混凝土表面降温幅度，抑制内部微裂纹的生成。

[1] 洪启超.工程断裂力学基础[M].上海：上海交通大学出版社，1987.

[2] 郭勇.裂纹尖端应力强度因子计算方法的工程应用研究[J].航空发动机，2007，33（3）：25－27.

[3] 范天佑.断裂理论基础[M].北京：科学出版社，2006.

[4] 朱伯芳.大体积混凝土温度应力与温度控制[M].北京：中国电力出版社，1998.

[5] 田明伦，黄松海，刘恩锡，等.混凝土断裂韧度[J].水利学报，1982（6）：38－44.

[6] 颜毅，肖伟，马占武.预应力混凝土箱涵结构理认分析及计算[J].交通科技与经济，2013，15（4）：1－4.