组合预测模型在铁路货运量预测中的应用

王 宁，徐志禹

（兰州交通大学 交通运输学院，甘肃 兰州 730070）

铁路货运量是指一定时期内以重量单位计算的由铁路实际运输的货物数量，它是货运市场中重要的基础数据，其预测结果直接影响到铁路运输计划以及有关运输政策的制定。目前，铁路货运量预测的常用方法很多，主要包括定性预测、定量预测以及两者相结合的综合预测方法。这些方法多是研究运输方式自身的发展规律，借以预测未来发展趋势。一般地，对于同一个预测对象，不同的预测方法往往能提供不同的有用信息，如果简单将预测误差平方和较大的一些方法舍弃掉，可能会丢失一些有用的信息。而组合预测更强调来源于不同信息的各种预测，而非构造复杂的单项预测，由于具有更高的预测性能，因此，出现极端预测误差的风险更小。

1 组合预测模型与原理

组合预测方法是将几种预测方法所得到的预测结果选取适当的权重进行加权均的一种预测方法，目的在于综合利用这些模型所包含的信息，尽可能地提高预测精度，增加预测结果的可靠性。同一货运量预测问题，可运用n种方法进行预测，yi为预测年度各种方法所得的预测值，组合预测方法的预测公式为

式中：λi为第i种预测方法的权重系数。

目前，应用较为广泛的是最优组合预测模型，常见的权重选取方法有：算术平均法、标准差法、方差倒数法、均方倒数法等。

2 单项预测模型的选取与建立

目前，铁路货运量预测常用的方法有时间序列法、回归分析法、灰色预测法等。时间序列法是根据预测对象的历史态势推测未来的发展趋势，该方法的优点是需要的数据信息量较小，方法简单易行；回归分析法的主要出发点是在数据信息充分完备的条件下，揭示出预测对象同相关经济变量之间的数量关系，用以预测对象的未来值；灰色预测法避开预测对象复杂的相互关系，着眼于预测对象本身的灰色信息，通过处理原始数据和建立灰色模型，掌握预测对象的发展规律，对预测对象的未来状态做出科学的定量预测，达到使灰色系统白化的目的。针对铁路货运量预测，选取几种预测模型进行试算，从预测计算结构来看，指数平滑、乘幂、一元回归和灰色模型进行组合预测具有较好的预测效果。下面选取2000～2010年铁路货运量历史统计数据进行建模计算，如表1所示。

表1 铁路货运量历史数据表

2.1 指数平滑模型

指数平滑模型是运用整个时间数列的全部资料，通过指数进行加权平均，对未来趋势进行预测。其常用的方法有一次指数平滑法、二次指数平滑法、三次指数平滑法等。其中，一次指数平滑预测模型为

式中：S（1）t为即本期（t期）的一次指数平滑值，yt为历史年度实际货运交流量数据，α为平滑常数，0＜α＜1。

二次指数平滑值S（2）t的计算公式为

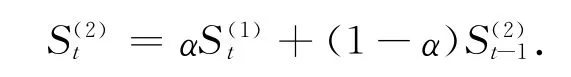
二次指数平滑线性预测模型为

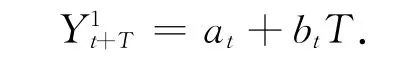
其中

式中：t为原始时间序列的最后一期，T为t期到预测期的间隔数，Yn＋T为第t＋T周期的预测值。

本文采用二次指数平滑模型进行计算。建立指数平滑模型的关键是选择合适的平滑系数α，由表1可见原数列波动不大、线性较好，根据经验α通常取0.1～0.3，经试算，当α取0.3时，误差较小，选取0.3进行计算。运用EXCEL计算可得铁路货运量二次指数平滑预测模型为

2.2 乘幂模型

乘幂预测模型的一般形式为

式中：y为预测值；b，m为模型参数（常数）。

运用EXCEL计算可得铁路货运量乘幂预测模型为

2.3 一元回归模型

回归分析预测法又包括一元线性回归预测法、多元线性回归预测法和非线性回归预测法等。本文选取一元线性回归预测模型，如果预测对象Y与相关变量X之间存在线性关系，可以用下式表示

式中：Yt为铁路货运量Y的历史数据，Xt为相关影响因素变量X的历史数据，a，b为待定参数。

影响铁路货运量的因素有很多，包括GDP、第三产业总产值、交通运输业增加值、居民交通类消费支出等。经各指标与铁路货运量相关性试算，结果表明货运量与GDP具有较高的相关性，因此，选取GDP作为模型影响因素变量X，其中GDP历史数据如表2所示。

与GDP相关的线性模型形式为

运用spss17.0软件建立铁路货运量对GDP的一元线性回归模型（见表3）。

表2 我国GDP历史数据表

表3 一元回归模型参数表

表3中给出了线性回归模型中的参数和常数项的估计值，其中常数项系数a为141092.34，回归系数为b，其数值为0.594，线性回归的标准误差为14210.52，标准化回归系数为0.971，回归系数 T检验的t统计量观察值为12.546，T检验的概率ρ应为0.000，小于0.05，所以，回归系数有显著意义。由此可得到铁路货运量一元回归模型为

其中，关于GDP未来年度的预测值的确定，到2020年我国国内生产总值将一直保持7.18%的年均增长速度。而按照国家统计局对今后几年的预测以及对国民经济实际运行情况的深入分析，今后几年我国国内生产总值年均增长速度极有可能为8.00%，因此，预测未来年度GDP是按照年均8%的增长率递增。

2.4 灰色模型

灰色系统理论预测模型的基本原理是：通过已知的历史数据列，进行累加生成，建立微分方程模型，预测将来年份的值。其中，最常用的是GM（1，1）模型。根据表1铁路货运量数据建立灰色模型

求解上述微分方程，得到的时间函数为

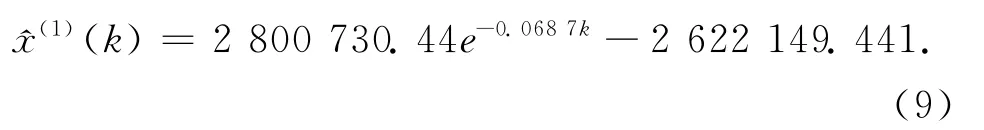
按照上述模型进行预测，再根据公式

得到原数据列的相应追溯预测值，以及未来年份的预测值。

3 铁路货运量组合预测

本文选用标准差法来确定加权组合预测模型的权数，其数学表达式为

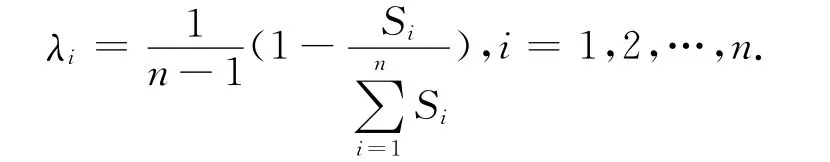
式中：Si为第i个模型的标准差。

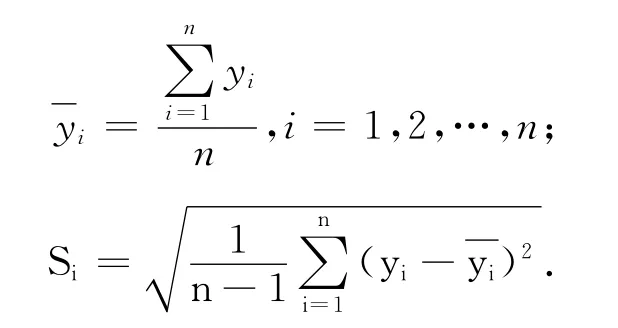
根据表1的数据，将以上4个单项模型的预测结果与实际值进行比较，计算预测标准误差，并把计算所得权重代入式（1），建立组合预测模型为

得出各模型预测货运量结果如表4所示。从表4中可以看到，各种模型预测结果与实际值的相关性都在0.95以上，说明以上预测模型拟合优度都较高，均具有很强的预测性。另外，组合模型标准误差10295.346为最小、相关性达到0.991为最高，该预测模型可信度提高了，可以看出组合模型比单项模型更优。

表4 各模型预测货运量结果与检验指标表万t

运用上述各预测模型对我国2011～2015年的铁路货运量进行预测，计算结果如表5所示，数据变化趋势的对比如图1所示。

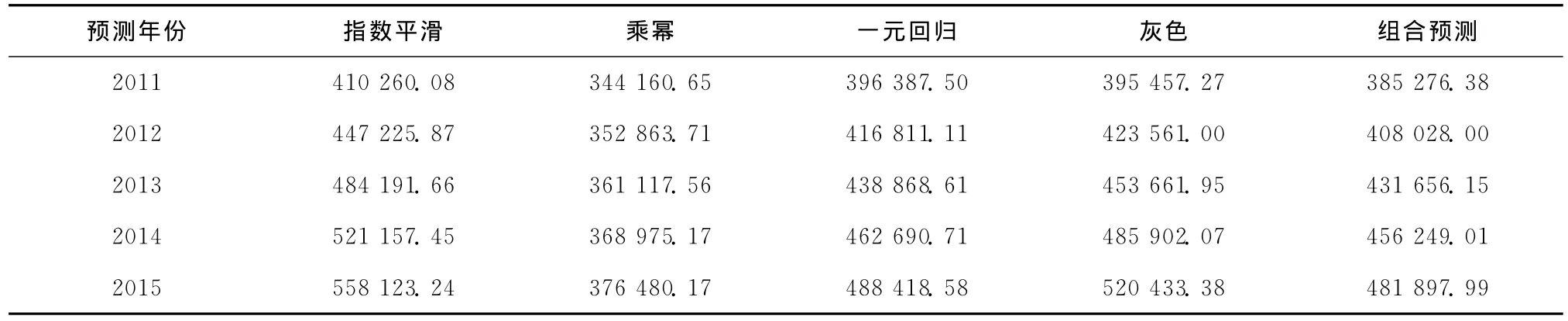
表5 各种模型铁路货运量预测结果表万t

图12000 ～2015年铁路货运量各种模型预测数据变化趋势

预测结果表明，在未来5年中，我国铁路货运量将不断增长，至2015年将达到48.2亿t，此预测值与我国“十二五”铁路建设规划的“2015年货运总量达到48亿t”基本接近。该组合预测模型针对短、中期预测的精确度、可信度是较高的。由于铁路货运是一个复杂的系统，会随着时间的推移，与用以建模的历史数据相联系的内部以及外部环境条件产生各种变化，甚至是突发性的变化，因此，该组合模型若用作长期预测还需要结合各种假定条件进行定性分析。

4 结束语

在铁路货物运输量预测中，单个预测模型进行运量预测必然存在一定的局限性。综合利用各个单项模型所提供的信息，运用组合模型进行预测，能在一定程度上提高预测精度，比单项模型更适合实际的铁路货运量预测。

[1] 朱章，庄建桥.对组合模型的再讨论[J].武汉工业学院学报，2002（2）：96－97.

[2] 李宝慧，项静恬.浅谈权重综合方法及组合预测[J].统计工作，2000，28（2）：28－29.

[3] 刘思峰，党耀国，方志耕，等.灰色系统理论及其应用[M].北京：科学出版社，2004.

[4] 李大为，俞晶菁，吕高腾，等.铁路集装箱短期运量预测方法分析[J].交通科技与经济，2012（5）：111－115.

[5] 孙敬，査伟雄.江西省公路货运量预测研究[J].交通科技与经济，2011（2）：35－38.