机器人最短路径最小时间路径分析

郑 文

（重庆电子工程职业学院，重庆 401331）

0 引言

现有一个800×800的平面场景图，在原点O(0,0)点处有一个机器人，它只能在该平面场景范围内活动。场景中有12个不同形状的障碍物，机器人移动时不能与之发生碰撞，障碍物的数学描述如表1所示。

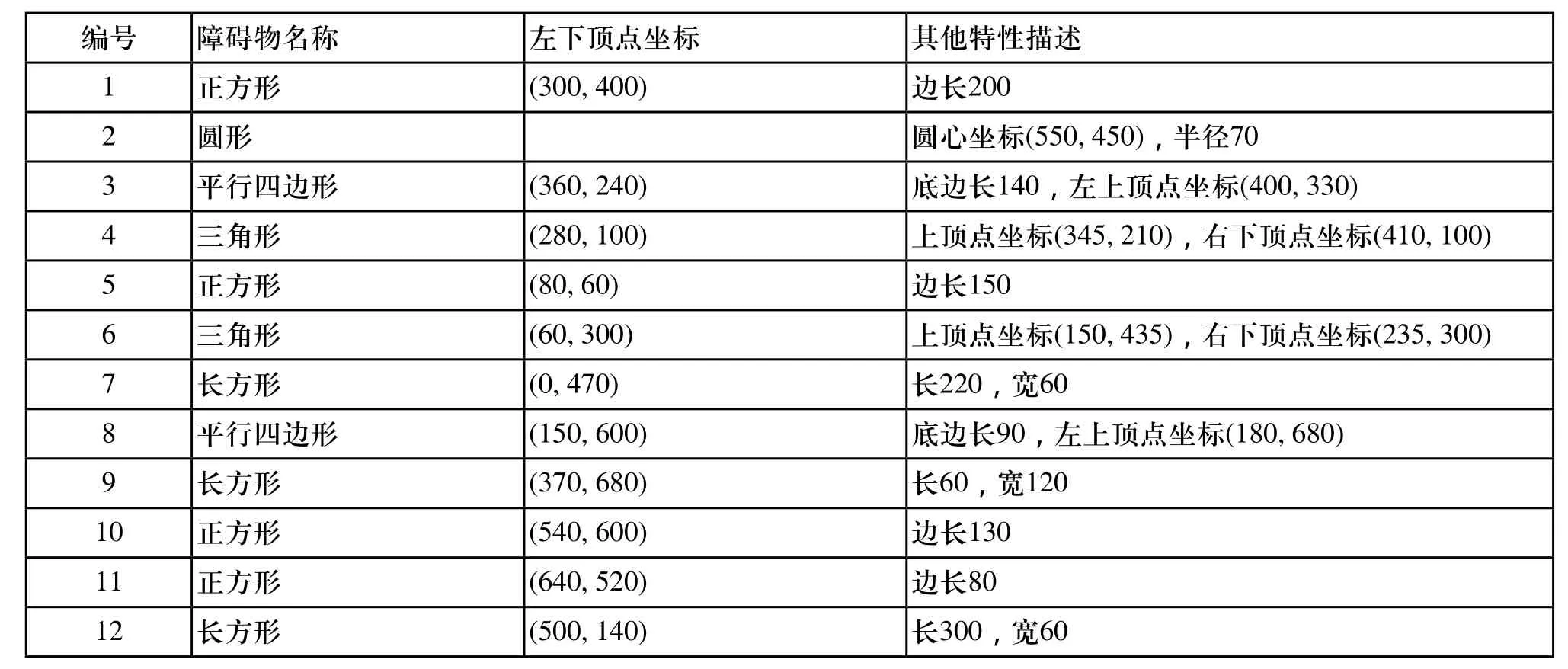
表1 障碍物的形状与位置

在平面场景图中，障碍物外指定一点为机器人要到达的目标点（要求目标点与障碍物的距离至少超过10个单位）。规定机器人的行走路径由直线段和圆弧组成，其中圆弧是机器人转弯路径。机器人不能折线转弯，转弯路径由与直线路径相切的一段圆弧组成，也可以由两个或多个相切的圆弧路径组成，但每个圆弧的半径最小为10个单位。为了不与障碍物发生碰撞，同时要求机器人行走线路与障碍物间的最近距离为10个单位，否则将发生碰撞，若碰撞发生，则机器人无法完成行走。机器人直线行走的最大速度为 v0=5个单位/秒。机器人转弯时，最大转弯速度为其中r是转弯半径。如果超过该速度，机器人将发生侧翻，无法完成行走。

通过建立数学模型来分析机器人在区域中从O ( 0 ,0)→ C (700,640)的避障最短路径和从O ( 0 ,0)→ A (300,300) 的最短时间路径。

1 问题的分析

1.1 机器人移动时的避障策略

图1 机器人的避障策略图

机器人在可行域内由起始点T ( 一个子目标)绕过障碍物W驶向目标点Q( 下一个子目标) 的过程中；要使经过的路径最短，在经过障碍物区域时应尽量贴近该障碍物, 绕过障碍物后，若目标在机器人的视觉范围内，应以直线移动的方式驶向目标点 Q[1]；如图1所示。

由于机器人不能折线转弯，所以转弯路径应由与直线路径相切的一段圆弧组成，由起点T经障碍物W到目标点Q的最短路径是：两直线段与圆弧长之和，即

1.2 机器人从起点ST到终点SQ的 可行路径

机器人从起点到终点的可行路径就是在可行域内（与障碍物至少保持10个单位的区域），寻找从起点ST 到终点SQ的安全避障路径所经过的一系列点的集合。

在障碍物数量有限的情况下，从起点到终点寻找一条可行路径的算法[2]如下：

步骤1 机器人由起始点ST 驶向终点SQ的过程中, vi和V分别表示第i个避碰点和避碰点的集合,初始条件

步骤2 机器人移动方向正对着终点SQ, 如果终点SQ在机器人的视觉范围内 , 执行步骤5, 否则执行步骤3；

步骤3 机器人搜索障碍物的周围区域, 并根据视觉信息决定避碰点 vi+1；

步骤4 机器人移动至 vi+1, 避碰点 vi添加到集合V中, i = i+1, 然后执行步骤2；

步骤5 机器人向终点SQ 移动, 当机器人到达终点SQ时, 就得到了一条从起点到终点的可行路。

以此规则来确定机器人在可行域中的行进路线。

按此算法，结合避障策略，作出机器人在可行域内从 CO→ 的行进路径，在避碰点处，机器人与障碍物相距10个单位,如图2所示。

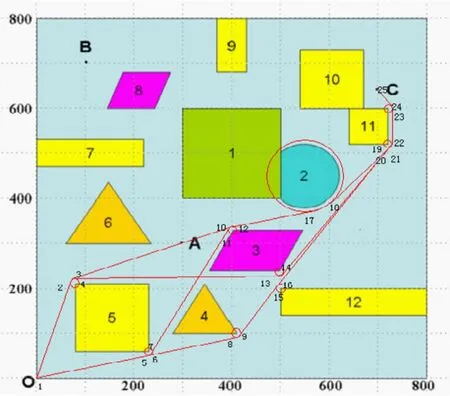
图2 机器人从 CO→ 的可行进路径

2 机器人从 O (0 ,0)出发， O → C 的最短路径

从图2可看出，从 CO→ 的可行路径构成了一个赋权网络图N．顶点集合：

为了表示的方便，图中的顶点用相应的数字表示。

应用求切点坐标的方法，求出V中各点坐标、圆弧圆心坐标、直线段及圆弧长．数据如表2所示。

表2 数据信息表

从O到C的最短路径问题就转化为在网络图N中找一条从O到C的最短路，以D表示从O到C的所有路径之集， )(Pd 表示路径P的长度，则得数学模型：

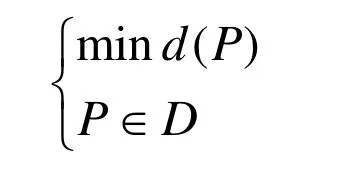
求解算法[4]如下：

设W为图N的带权邻接矩阵， ()lv表示从顶点 0u到v的一条路的权， ()zv表示v的父节点，用以确定最短路的路线。

根据上述算法求出的 ()lv就是0u到v的最短路的权，从v的父节点标记 ()zv追溯到0u，就得到0u到v的最短路的路线．用matlab语言编程可求得：

机器人从O移动到C的最短距离为：

3 机器人从 O ( 0,0)出发， O → A 的最短时间路径

3.1 从起点ST 到终点SQ最短时间路径分析

在圆弧上机器人的移动速度v与圆弧半径r有如下关系：

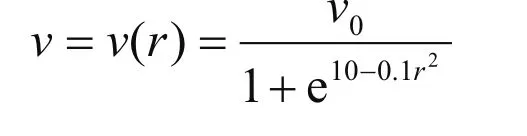
其中v0是直线段上的移动速度。由于，所以移动速度v是圆弧半径r的增函数；因圆弧长L= r θ，所以在圆弧上，移动速度随圆弧长的增大而增大；因此机器人从起点到终点的最短路径并非最短时间路径。下面建立最短时间路径模型。

图3 机器人从避障物i经过避障物j的行进路线

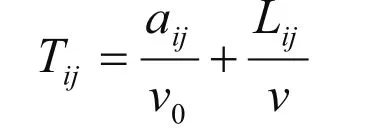
由于切点、圆弧长与半径r有关，所以aij、Lij、v都是半径r的函数，从而Tij是半径r的函数．

我们引入0-1变量来选取从起点ST到终点SQ 的路径经过的转弯点，令

则从起点到终点路径的时间为

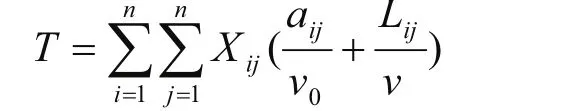
所以从起点ST 到终点SQ的最短时间路径模型可表示如下

由于障碍物所处的位置不同，对切点的限制条件也就不一样，所以对每个避障点的限制条件应具体问题具体分析。

3.2 机器人从 O ( 0,0)出发， O → A 的最短时间路径分析

从图4可看出，从 O → A 有两条可行路径 P1、P2可走,因此最短时间目标函数为：

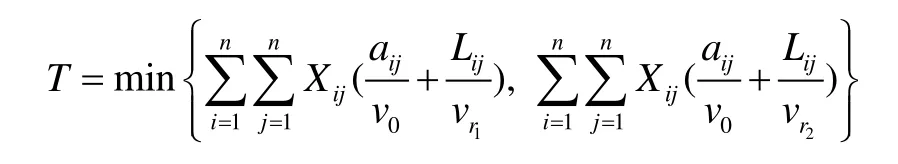
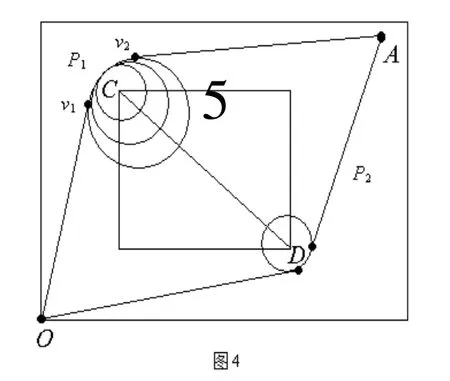
图4 机器人从 AO→ 的最短时间路径分析图

先分析在 P1段上的最短时间路径，如图4所示，设圆心坐标为 ( x0,y0)，半径为r，是圆弧上连接点 O ( 0,0)和 A ( 300,300)的两个切点． P1是机器人从O移到A的一条可行路，顶点集合 V = { O ,v1,v2,A}．从O到A的移动时间是两直线段上的移动时间与圆弧上的移动时间之和

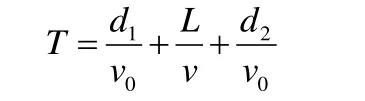
约束条件:障碍物5左上角的顶点与圆弧的距离大于等于10、两直线段与园相切、切点 v1、 v2的选择。

于是，可行路径 P1的优化模型如下:

下面我们采用搜索的方法，借助计算机来求解模型。

根据避障策略，机器人在经过障碍物区域时应尽量贴近该障碍物,在圆弧的半径发生改变时，我们始终保证圆弧距障碍物的最近距离是10个单位．因此圆心只能在CD上，且由C向D移动，如图4画出的几个圆。

下面以C(80,210)为障碍物点，找机器人在路径 P1上移动的最短时间，搜索算法如下：

步骤1：用matlab命令solve求出切点 v1、 v2的一般性坐标。令初值r=10，增量Δr=0.1。

步骤2：当r＞220时，转步骤5，否则转步骤3。

步骤3：1）计算下一个园的圆心坐标：

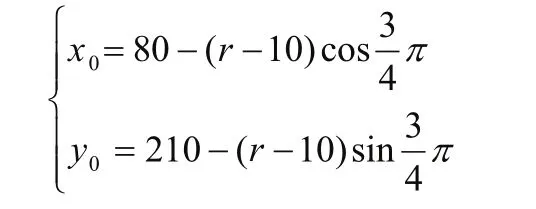
2）判断并计算切点1v、2v的具体坐标，计算圆心角θ。

3）计算直线段1d 、2d及弧长θrL=，圆弧上的移动速度v。

4）计算时间。

5）记录切点 v1、 v2的坐标、圆心坐标、半径、时间。

步骤4：回到步骤2。

用matlab编程求解，运行程序得：

最短时间T1=94.2283秒；

最短时间路径：

圆心坐标(80.28,209.72)，圆弧半径r=12.4，圆弧上的速度 v = 4.995。

与求在可行路径 P1上的最短时间一样，可求得在可行路径 P2上的最短时间是T2=96.5632秒。

所以从 O → A 的最短时间T = min{T1,T2}=94.2283秒，最短时间路径如上所述。

4 结束语

由于机器人在圆弧上的移动速度随圆弧半径的增大而增大，所以机器人从起点到终点的最短路径并非最短时间路径；从 O → A 可看出，移动距离是半径的增函数；当r＜r0=12.4时移动时间是半径的减函数，当r＞r0=12.4时移动时间是半径的增函数，r0=12.4是移动时间的极小值点；所以在从起点到终点路径的选择上，应在距离和时间上作权衡，做出决策。

[1] 金秀慧,伊连云.基于通用运动学模型的移动机器人避障路径规划[J].机械工程师,2005,12.

[2] 罗熊,樊晓平.具有大量不规则障碍物的环境下机器人路径规划的一种新型遗传算法X,机器人ROBOT,2004.

[3] 席志红,原新.基于视觉的移动机器人实时避障和导航哈尔滨工程[J],大学学报,2002.

[4] 赵静,但琦.数学建模与数学实验[M].高等教育出版社 2010.

[5] 任善强.数学模型(第二版)[M].重庆大学出版社,1993.

[6] 王学辉.Matlab 6.1[M].中国水利水电出版社.2002.