一种差动轮式竞赛机器人的路径跟踪方法

贺洪江，钟志贤

(1. 河北工程大学 装备制造学院，邯郸 056038；2.河北工程大学 信息与电气工程学院，邯郸 056038)

0 引言

随着机械设备自动化程度的提高，移动机器人的应用领域也越来越广泛。竞赛机器人也作为机器人学的一个重要分支，对其的跟踪控制也得到了广泛的研究。在差动轮式自主移动竞赛机器人路径控制中，主控制器通过连续采集编码器脉冲，记录机器人走过的真实里程。要对路径进行跟踪控制还需要机器人的实时角度，可以使用陀螺仪测得，但是由于陀螺仪成本高，易受环境影响[1]。针对上述问题，本文介绍一种只基于两个对称安装的编码器作为传感器的闭环路径控制方法，为以后多传感器信息融合进行路径规划提供物理实现的保证。

1 编码器安装和系统组成

两轮差动驱动的移动机器人的底盘结构示意图如图1(a)所示，左右两轮由两个电机驱动，前轮是一个可以自由转动的角轮。两编码器轴上装上轮子，做成随动码盘轮,对称地安装在底盘上，并有弹簧机构使其在随动过程中接地良好不被悬空。

在机器人的路径控制中，对直流电机转速和位置的控制有较高的要求，有高精度的电机控制，才可以知道自己的位置和跟踪自己要行走的路线。所以系统采用专用电机控制盒对电机进行转速控制。控制系统的组成如图1(b)所示。

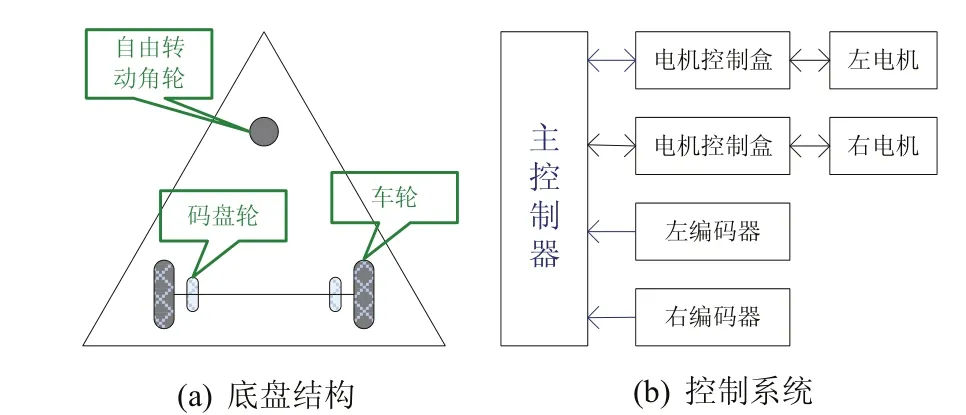
图1 系统结构

2 编码器采集距离和角度

2.1 实时距离换算

机器人运动过程中编码器A、B线输出波形如图2所示。

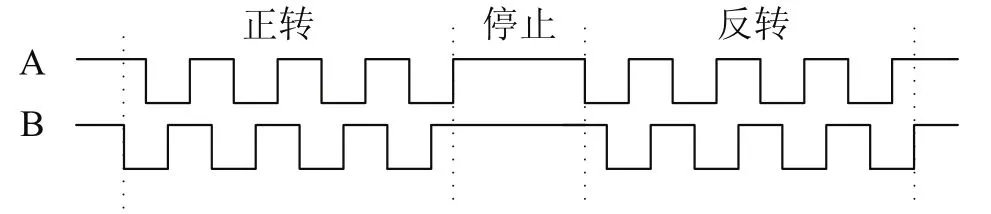
图2 编码器输出波形

1）单边沿采集方法：把A线接到主控制器外部中断，下降沿触发，在中断服务程序中判断B线，若B线为低电平则正转，脉冲计数加加，若B线为高电平则反转，脉冲计数减减[2]。

2）双边沿采集方法：同样把A线接到主控制器的外部中断，双边沿触发，在中断服务程序中先判断B线，若B线为高，再判读A，若A也为高则表示正转，脉冲计数加加，若此时A为低则表示反转，脉冲计数减减。若进中断后先判读的B线为低，则返回。

实际应用中，有时机器人在看似静止的情况下，由于机器人的微动编码器输出的波形会在某一边沿来回跳变，此时若采用单边沿采集则会造成脉冲计数的错误递增或递减，而双边沿采集方法可以相抵消，避免机器人停止时，却有里程值改变的问题。

编码器采集到的脉冲数与里程成正比例关系。因此，可以由脉冲数转化为里程值。分别对左右两个编码器进行标定，即找到脉冲数与里程值的比例系数。采用多次测量取平均的方法减小误差。实验中机器人5次行走2m测得的脉冲数如表1所示。

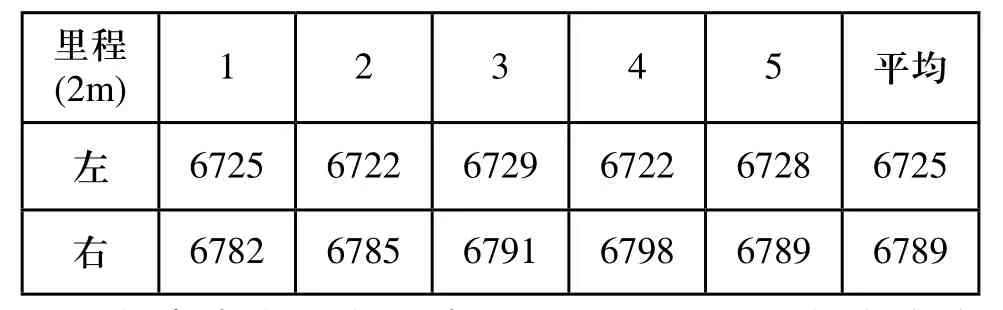
表1 左右码盘标定实验数据

程序中左里程值表示为：Dis_L = 左脉冲数× 2000 / 6725 (mm)；

程序中右里程值表示为：Dis_R = 右脉冲数× 2000 / 6789(mm)；

车体的总里程为左右里程的平均值，表示为：Dis_M=( Dis_L+ Dis_R)/2。

2.2 实时角度换算

由于是对称安装，左右两车轮的运动轨迹可以用左右两码盘轮的运动轨迹来等效。根据左右两个码盘采集的里程值，在保证两码盘不离地的情况下，根据弧长公式计算出车体转过的实时角度，方法如图3如示。

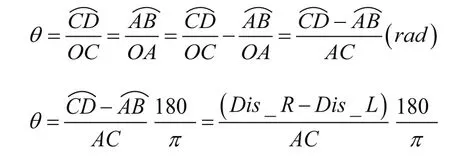
其中，Dis_R为此时机器人右码盘记录的里程，Dis_L为此时机器人左码盘记录的里程。

具体应用时标定车体的初始朝向为0，则向左转过的角度为正值，向右转过的角度值为负值。

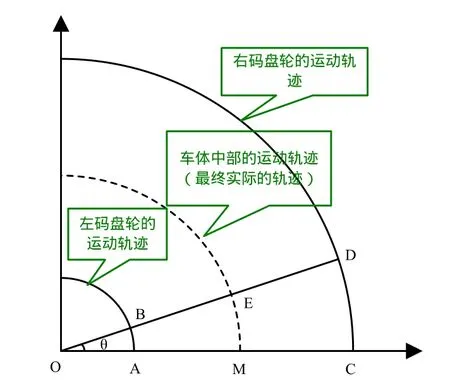
图3 角度换算示意图

3 直线、弧线跟踪控制

3.1 直线跟踪

控制中所用的到距离和角度均来自双编码器的计算。在程序中采用经典PID控制，主控制器根据随动编码器得到的信息进行PID计算，结果输出给电机控制盒控制电机。理想情况下，若机器人严格进行直线运动则左右两个编码器采集的里程值之差因该为0或者为某一常量，所以把两编码器采集的里程之差作为跟踪控制的量，0或某一常量作为设定值，进行PID控制。但是实际对于直线行走的PID校正，误差的形式有两种：角度误差θ和中心位置误差d。

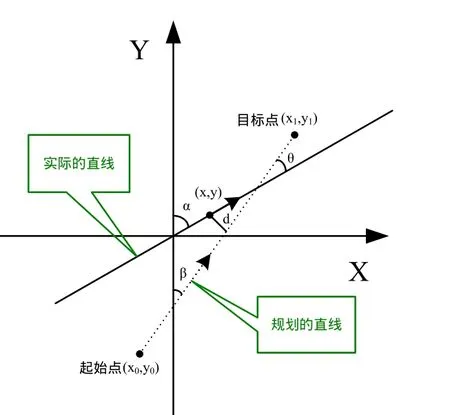
图4 直线跟踪示意图

如图4所示，直线行走时机器人的当前朝向角为α，β为规划好的直线在坐标系中的角度，由平面几何可得下式：

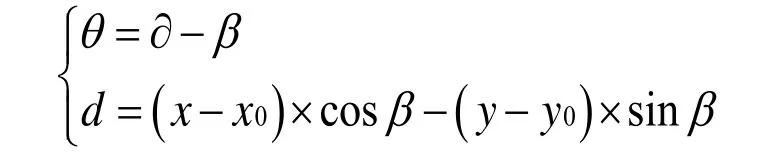
θ和d这两个误差相对独立，可以分别进行检测控制，这里为了减少PID参数整定，通过加权将他们合成一个误差e，只用一套PID参数进行校正，即把e作为检测值，0作为设定值。如下所示：e=d+kθ。

加权系数k反映了机器人角度误差与位置误差相涨或者相消的程度，实际上它还包含了一定的微分的意义[3]。

对于综合后的总误差e，我们采用增量式PID算法对其进行校正,在程序中具体实现的函数名为：

INT32S PID_common(INT32S set, INT32S feedback, PID_Uint *p);

其中，入口参数分别为，设定值(set)，检测值(feedback)，和指向PID参数结构体(PID_Uint)的指针。

根据开环实际测试，可以估算得出角度偏差和位置偏差的加权系数为3，在实际调试时也验证了这个权值是合适的。在实际应用时还需给出，起始点坐标和目标点坐标，加减速距离，起始速度，最高速度和末速度，然后根据增量式PID校正算法，对机器人的左右轮速度进行实时地校正。实现沿规划好的直线行走。

3.2 弧线跟踪

类似直线的跟踪思想，算法的参考目标是转弯半径R和机器人相对初始朝向的实时转弯角度θ，在这两个参照量和实际测得的机器人状态的偏差之间做加权求出总误差e，减少参数个数，以方便参数的调试。跟踪示意图如图5所示。

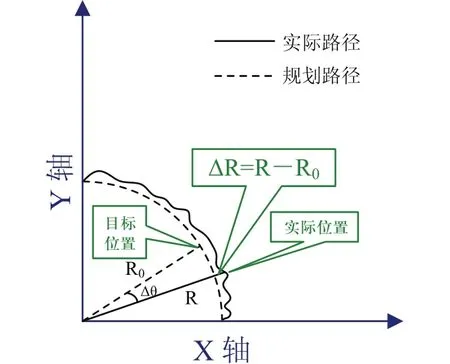
图5 弧线跟踪示意图

e = D R + k × Dq ，ΔR为实时测得的半径和规划给出的半径之差，Δθ为规划的圆弧计算出的应转的角度和由双编码器计算反馈回来的自身角度之差。如图3所示，计算实时车体运动半径公式如下：

其中：半径R为OM的长度。

具体应用时，应根据事先给定的弧线路径信息，先计算得出左右两轮的初始基速度，两者应该对应成比例，再此基础上运用增量PID算法对跟踪过程中产生的总误差e进行调节。要实现快速转弧，在高速且转角较大度时，还应逐渐增大两轮的差速，并在距目标角度还有一定的误差时，逐渐减小两轮差速以实现行走过程的流线衔接和平稳过渡[4]。

4 终点准确定位

通过直线和弧线的组合就可以控制机器人走复杂的路径。最后停车时由于场地摩擦系数的不确定性，即使在到达终点附近就开始减速，由于惯性机器人可能往往会超过设定的终点才停下来，所以终点准确定位不像行走过程中的那样只把左右轮差速作为被控对象，而机器人的左右轮差速和左右轮基速度都成了被控量。机器人的初始基速度是根据实际情况事先设定的。在终点准确定位控制中，都采用闭环PID控制。控制框图如图6所示。

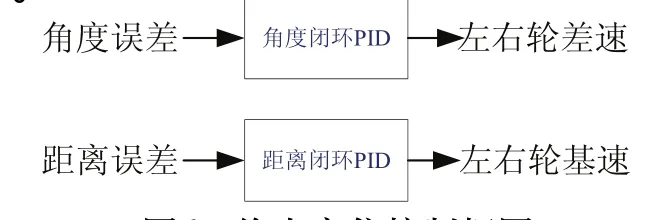
图6 终点定位控制框图

5 实验结果和分析

表2 机器人跟踪轨迹误差比较（10次测试的实验结果）

由测试结果可以看出，基于双编码器计算角度和距离控制机器人跟踪事先设定好的路径的方法可行，平均误差都在100mm以内，基本可以满足竞赛机器人要求。在测试过程中，由于左右轮电机控制盒发送速度需要时间，所以控制程序的控制周期设定较大，在20ms左右，使控制效果得不到充分实现。另外左右两个电机控制盒的速度不能被同时设定，所以在控制周期内轮流改变对两个控制盒的发送顺序，可以改善控制效果。

[1] 李世华,田玉平.移动小车的跟踪控制[J].控制与决策,2000,15(5): 626-628.

[2] 鲜浩,任爱芝,盛仲飚.增量式编码器数据采集[J].华北工学院学报,2003,24(2):142-143.

[3] 吴卫国,陈辉堂,王月娟.移动机器人的全局轨道跟踪控制[J].自动化学报,2001,27(3):326-331.

[4] 龚建伟,陆际联,黄文宇.轮式移动机器人航向跟踪预估控制算法[J].机器人,2001,(3):193-196.