多平台传感器跟踪系统无序量测滤波器设计

张 举（中国电子科技集团公司 第二十研究所，陕西 西安710068）

0 引言

现代海战中，超低空突防的来袭导弹已构水面舰艇的主要威胁，而单平台的侦察探测能力不能满足反导作战的要求，在此背景下，充分利用多平台传感器的信息共享可以提高其反导效果。当采用多平台传感器探测的数据进行融合时，由于不同类型的传感器的采样率、预处理时间以及数据通信延迟，导致出现多个传感器量测无序到达融合中心的现象[1]，即无序量测现象。由于Kalman滤波算法只适于处理顺序量测，因此基于Kalman滤波框架的量测融合算法不能直接处理状态估计的负时间更新问题。当前针对无序量测现象的滤波方法主要有：丢弃延迟量测法、重新滤波法、数据缓存法和直接更新法[2]。丢弃延迟量测法会造成大量信息丢失，导致目标跟踪精度下降甚至丢失目标。对于重新滤波法，存储量和计算量随传感器数目、目标数目及延迟时间的增长而显著增加。数据缓存法需要较大的存储空间而且输出严重滞后。直接更新法直接使用无序量测更新当前时刻的状态估计，使其达到或逼近量测顺序处理时的滤波精度[3][4]。

1 问题描述

对于协同作战的多平台系统，每个协同单元在自身坐标系下进行目标跟踪的同时，接收其它平台周期性发送探测信息。

状态方程和测量方程如下：

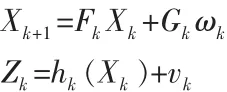
其中，ωk～N（0，Qk）为建模误差，vk～N（0，Rk）为测量误差。 矩阵 Fk为状态变换矩阵，Gk误差输入矩阵，Xk包含目标位置、速度和加速度。

线性测量方程可通过对非线性观测函数线性化：

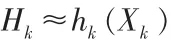
其中，Xk＝［xkykzkx˙ky˙kz˙k］T

对于扩展卡尔曼滤波器的滤波方程如下：

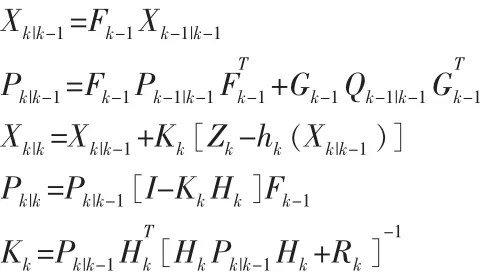
下面在时间轴下，给出采用离散时间扩展卡尔曼滤波的负时间更新的情况。如图1，用tk-2时刻的测量数据Zk-2，得到标准滤波器推导状态估计值Xk-2/k-2。tk-1时刻遥控传感器获得测量值Zk-1，把这些数据添加时戳tk-1，并提交数据到具有传输延时的网上。tk时刻测量值Zk准时到达，并更新状态估计由Xk-2/k-2得到Xk/k。由于数据延时，测量值Zk-1在tk+时刻到达，把该延迟数据考虑进去用于提高状态估计Xk/k+。

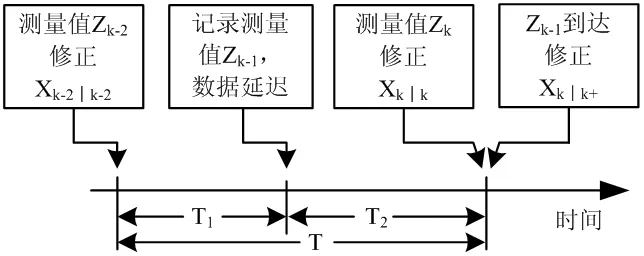
图1 负时间更新时间轴

基于上述问题表述的负时间更新算法推导如下：

2 滤波模型推导

2.1 状态推导

时间间隔表示为：

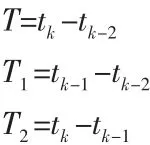
状态Xk|j估计误差表示为，相应真值表示为状态Xk，则

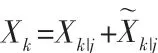
时间间隔T内，状态Xk∈Rn的离散时间推导表示为：

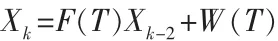
其中，F是离散时间状态转换矩阵，W（T）是对象噪声影响的矢量Xk＝［xkx˙k］T表达式，假定状态矢量 是一维向量，那么状态变换矩阵为：

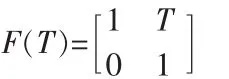
该模型的对象噪声将为连续时间白噪声加速度。单位脉冲加速度δ（t-α），tk-2＜α＜tk，将在在状态空间［tk-2-α 1］T产生响应。 白噪声加速度ω（α）应用整个时间间隔T产生对象噪声：

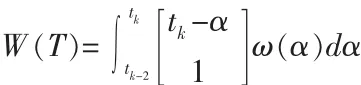
从tk-2到tk状态估计协方差的时间映射为：

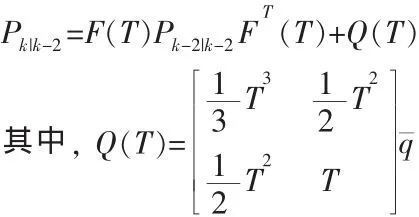
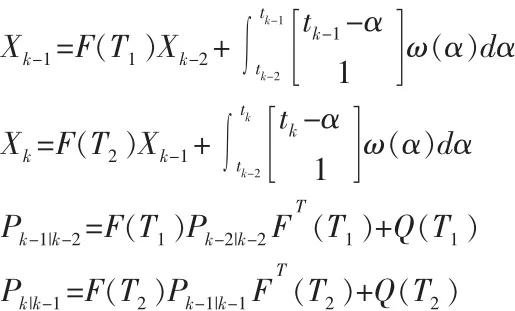
2.2 tk时刻用 Zk值更新

当测量值Zk到达滤波器用于处理时，滤波器并不知道延时测量值Zk-1的存在。因而，滤波器将继续用标准卡尔曼滤波器更新处理。

首先处理将设计以前的状态估计Xk-2

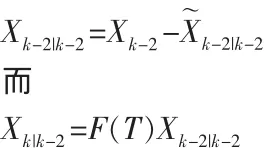
则状态估计误差为

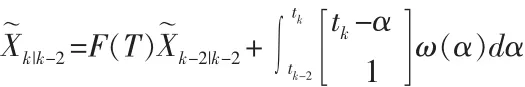
标准卡尔曼滤波处理应用增益更新状态估计

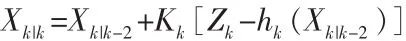
进而可求得

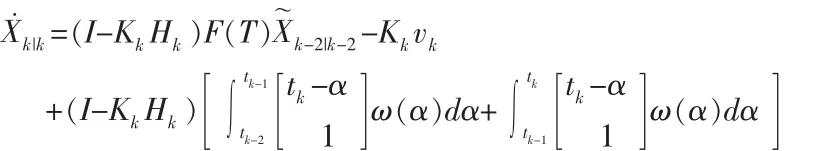
考虑到突发性，负时间更新可能在Xk-2|k-2→Xk|k更新时刻，定义量

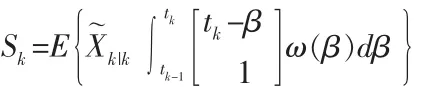
该量为协方差，tk时刻标准更新后的状态估计误差X˜k|k，时间间隔T前半部分的累积对象噪声误差。通过整理可得：

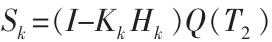
2.3 负时间更新算法

延时测量 Zk-1具有误差 vk-1～N（0，Rk-1），在状态估计更新 Xk|k被发现时，时刻状态估计更新Xk|k+。下面确定的卡尔曼增益新Kk+

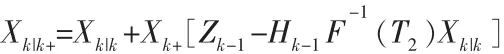
该项F－1（T2）Xk|k于计算tk-1时刻更新的新息，同时确保 tk-1时刻的估计值Xk|k+。 代入Zk和 Xk，则

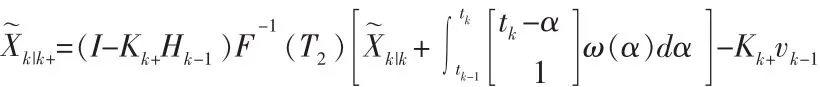
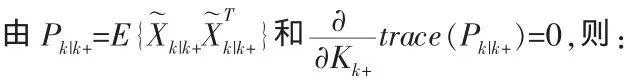
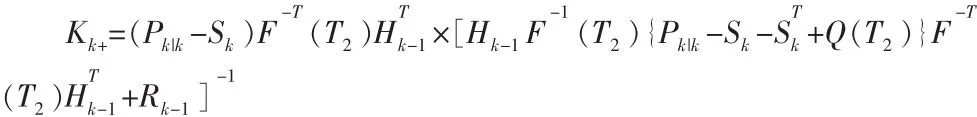
进而求得

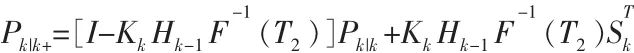
3 简单算例

这里只用目标跟踪的其中一个坐标，滤波器参数为：

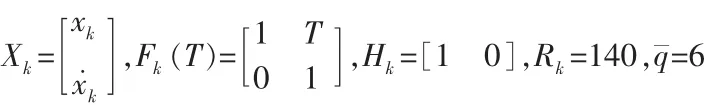
假定有4个测量值Zk，k=1，2，3，4，所有值的准时到达在1秒的间隔内。

为了对比分析最小均方差负时间更新方法和标准卡尔曼滤波公式的滤波结果，表1给出了三种不同情况下的最终协方差值：无延时测量值、缺失测量值Z3标准扩展卡尔曼滤波方法和Z3最后到达的负时间更新滤波方法。

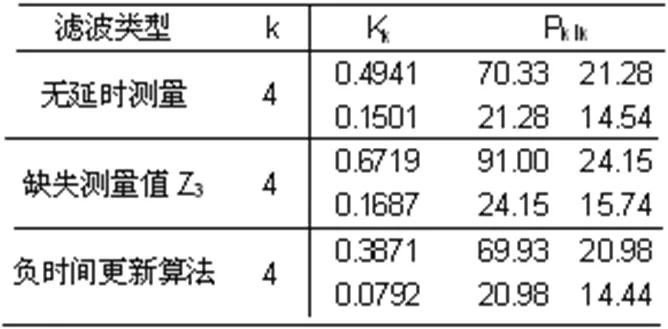
表1 三种不同情况下最终协方差值

由表1可知，丢弃延时量Z3情况下，时间间隔增加到2秒，协方差值变得很大，滤波增益也很大；采用负时间更新方法滤波得到的最终协方差值与无延迟测量值的扩展卡尔曼滤波值近似是一样的。

4 结论

本文针对多平台传感器目标跟踪的无序量测问题，给出了最小均方差负时间更新法的推导过程，并用简单的例子验证了采用负时间更新算法能够取得较好的结果。

［1］韩崇昭，朱洪艳，段战胜，等.多源信息融合[M].2版.北京：清华大学出版社，2010.

［2］黄细凤，吴钦章.顺序更新式无序量测处理算法[J].传感技术学报，2012，2，25（2）.

［3］Bar Shalom Y.Update with Out-of-Sequence Measurements in Tracking：Exact Solution[J].IEEE Transactions on Aerospace Electronic Systems，2002，38(3)：769 －778.Hilton R D，Martin D A，Blair W D.

［4］Tracking with Time Delayed Data in Multi-Sensor Systems[R].Technical Report NSWCDD/TR－93/351，AD－A355269，Dahlgren，VA，August 1993.