水深对船舶摇荡运动影响的数值方法研究

吴 晞 韩晓光 李宇辰

（1.海军陆战学院训练部 广州510430；2.海军陆战学院研究生队 广州510430）

0 引 言

船舶在浅水状态下航行时，随着水深与吃水之比的减小，其运动特性会发生较大变化。浅水时船舶周围的流场发生变化，主要反映在船侧、船底的流速比深水时大，致使粘性阻力增加，同时，由于船底的流速增加、压力降低，从而使船的吃水增加和船舶的航态发生变化［1］。

随着船舶发展趋势的大型化和高速化，船舶的速度越来越快，吃水越来越深，船舶在港口附近或浅海发生触底、搁浅的概率不断增大，浅水对摇荡运动的影响是船舶安全操纵所需考虑的重要因素。本文采用浅水域条件下的三维势流理论对某NPL型船在不同吃水条件下的纵摇和垂荡运动进行计算，总结了船舶纵摇和垂荡运动幅值响应函数随吃水深度变化的规律。

1 计算理论

1.1 三维势流理论

根据线性假设，船舶在波浪中速度势按叠加原理可分为定常势和不定常势2部分。定常部分不考虑波浪影响，是船在静水中稳定到定常状态后的速度势，这部分速度势与时间无关，把它从总速度势中分离出来，其余的非定常部分，记作ΦT（x，y，z），速度势的分解如下式所示［2］：

式中：ΦS为定常势；ΦT为不定常势；ΦT可以分解为入射波势、辐射势和绕射势3部分，这样下面的表达式成立

式中：ΦI为入射势；ΦR为辐射势；ΦD为绕射势；入射波势φ0为已知的；ω为波浪的遭遇频率；ηj为第j个运动模式的运动复幅值；φj为第j个运动模式单位幅值的摇荡运动的速度势。

1.2 速度势与流体力的求解

速度势所满足的条件如下。

［R］：远离物面的自由面上的波向后传播式中：n为物面上点的广义法向量；［L］为控制方程；［S］为物面条件；［F］为线性化的自由表面条件；［B］为底部条件；［R］为远方的辐射条件。

辐射势φj（j＝1～6）和绕射势φ7可以通过三维源汇分布理论，采用边界元法求解，一般的速度势可以表示为

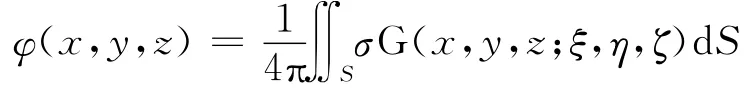
式中：σ为源强；S为入水结构面；（x，y，z）为流场中域点的坐标；（ξ，η，ζ）为S上源点的坐标；G为格林函数。

1.3 运动方程的建立

在随船平动的坐标系下，利用微幅、线性化的的假设条件，船舶在波浪中的运动响应X（ω）是通过下面方程［4－5］得到式中：Ms为结构质量矩阵；Ma为附加质量矩阵；C为线性阻尼矩阵；K为系统刚度矩阵；F（ω）为波浪力。

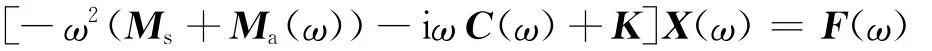
1.4 频率响应函数

本文计算中用到的幅值响应函数的定义如下

式中：φa为纵摇幅值；za为垂荡幅值；ζa为波幅；ω为波浪圆频率。

2 计算对象

2.1 模型参数

本文选取一艘NPL型船作为计算对象，计算对象的主要船型参数见表1。计算对象的型线数据使用AutoCad软件格式进行存储，各站的横剖线图见图1。

表1 计算对象的主要参数Tab.1 The main parameters of the calculate object

建模与计算工作采用Ansys软件平台。其中，建模采用 Workbench软件模块，将计算对象的型线数据导入并放样，并指定了水线的位置，计算对象建模后的三维效果图见图2。

基于Icem软件模块对计算对象进行网格划分，采用混合网格的划分方法，对曲率变化过大的部分进行了局部加密处理，曲率变化较平缓的部分采用四边形网格划分方法；从长宽比、最大折角等几个方面对划分后的网格进行了统计分析，计算对象的网格划分结果满足计算的要求。对计算对象进行网格划分后的效果图见图3。

图1 计算对象各站横剖线图Fig.1 The computational object station in a cross－sectional chart

图2 计算对象三维模型Fig2 The three－dimensional model

图3 计算对象网格划分结果Fig.3 The mesh of calculation object

3 计算结果及分析

考虑到计算对象在静水中正常排水条件下的吃水为2.226 m，本文分别选取4、6、8 m以及无限水深等4种不同的相对吃水情况作为计算的水深条件［6］，为全面分析水深对船舶摇荡运动的影响，选择10、15、20 kn等3种不同航速作为船舶在浅水中运动的航速条件。其中，模型在4 m水深、1 m波高条件下的表面波浪压力分布情况见图4，其他情况的波浪压力分布情况不再列举。

在不同水深条件下，垂荡运动幅值响应函数随波浪频率变化情况［7］如图5～7所示，比较3种不同航速下的垂荡运动幅值随水深的变化规律，在船舶低速且波浪频率较低的情况下，水深越深，垂荡运动的幅值响应越大；在航速较高且波浪频率较低的情况下，水深对垂荡的影响不大；在较高的波浪频率条件下，不论是低速还是高速的情况，均表现出水深越大，垂荡运动的响应函数越大的规律；从幅值响应函数的大小来看，在各种水深条件下，高速时的垂荡运动幅值响应要明显大于低速时的垂荡运动响应，所以，在浅水域下航行时，要特别注意对航速的控制，尽量采用低速航行［8］，以免发生剧烈的垂荡现象。

图4 船体表面波浪压力的分布情况Fig 4 Wave pressure distribution of the hull surface

图5 不同水深下垂荡运动的RAO（V＝10 kn）Fig.5 The heave RAO in different water depth（V＝10 kn）

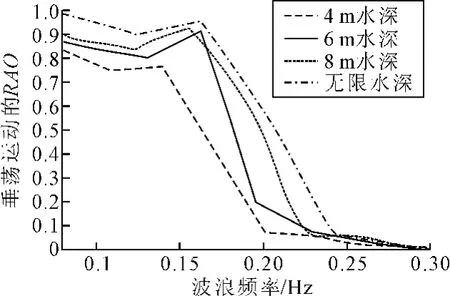
图6 不同水深下垂荡运动的RAO（V＝15 kn）Fig.6 The heave RAO in different water depth（V＝15 kn）

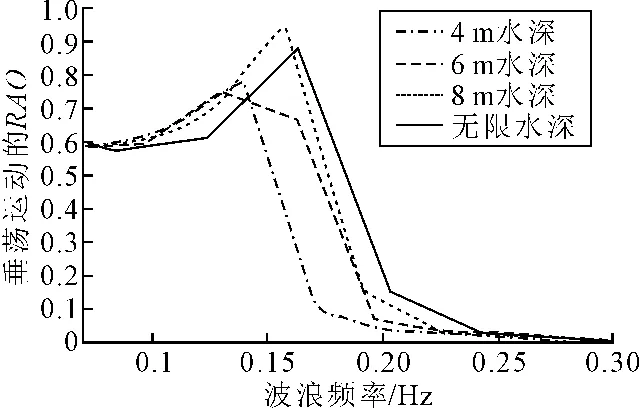
图7 不同水深下垂荡运动的RAO（V＝20 kn）Fig 7 The heave RAO in different water depth（V＝20 kn）

在不同水深条件下，纵摇运动幅值响应函数随波浪频率变化情况［9］见图8～10。从图中不难发现，当波浪频率较低时，水深越浅，纵摇运动幅值越大，水深越深，纵摇运动幅值越小；当波浪频率较大时时，水深越浅，纵摇运动幅值越小，水深越深，纵摇运动幅值越大；当波浪频率大于各0.25 Hz以后时，各种水深条件下纵摇幅值响应大小均随着波浪频率的增加而降低直至小到可以忽略不计；比较3种不同速度下的纵摇运动受水深的影响情况来看，同等水深与同等波浪频率条件下，航速越快，纵摇运动的幅值响应函数便越大，同垂荡运动的情况类化，在浅水中降低航速同样有助于减少船舶的纵摇值。

图9 不同水深下纵摇运动的RAO（V＝15 kn）Fig 9 The pitch RAO in different water depth（V＝15 kn）

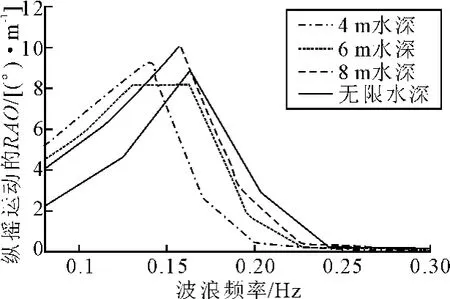
图10 不同水深下纵摇运动的RAO（V＝20 kn）Fig 10 The pitch RAO in different water depth（V＝20 kn）

4 结束语

随着船舶航运事业的发展，航行的经济性和安全性越来越受到人们的重视，浅水效应对船舶航行的经济性和安全性都有一定影响。通过某NPL瘦长型船舶在不同水深条件下纵摇和垂荡运动的规律计算和总结，进一步证实了浅水对船舶摇荡运动的影响，通过计算数据定量地揭示了浅水对船舶摇荡的影响程度，相信本文计算结果可以为船舶驾驶人员判断浅水效应对船舶摇荡运动的影响程度提供一定的理论参考。

［1］ 盛振邦，刘应中.船舶原理［M］.上海：上海交通大学出版社，2003.

［2］ 李积德.船舶耐波性［M］.哈尔滨：哈尔滨工程大学出版社，2007.

［3］ 戴遗山，段文洋.船舶在波浪中运动的势流理论［M］.北京：国防工业出版社，2008.

［4］ Noblesse F.The green function in the theory of radiation and diffraction of regular water waves by a body［J］.Jour.Eng.Math.，1982，16（12）：137－169.

［5］ Noblesse F.Interal identities of potental theory of radition and diffraction of regular water waves by a body［J］.Jour.Eng.Math.，1983，17（1）：1－13.

［6］ 吴建康，陈 波.采用Green－Naghdi方程和有限元计算浅水船波［J］.中国造船，2003（1）：17－23.

［7］ 娄 敏，董文乙，郭海燕.波浪作用下海洋立管试验研究及 ANSYS数值模拟［J］.中国造船，2010（1）：73－77.

［8］ 张志宏，顾建农，郑学龄，等.航行船舶在浅水水底引起的压力变化［J］.中国造船，2002（2）：9－12.

［9］ 杨剑文.航行船舶在浅水中的纵倾变化研究［J］.中国水运，2011（11）：1－4.