基于“各向异性”四面体网格聚合的复杂外形混合网格生成方法

赵 钟，张来平，2，赫 新，2

（1．中国空气动力研究与发展中心 计算空气动力研究所，四川 绵阳 621000；2．空气动力学国家重点实验室，四川绵阳621000）

0 引 言

在CFD工业化应用中，生成计算网格一直占据整个计算流程的60%～70%时间，这一点对于复杂外形高质量粘性流动计算网格的生成更为突出［1］。

依照网格的拓扑结构，计算网格分为结构网格和非结构网格。结构网格的优点是数据结构简单，存储方便，计算简单快捷，计算结果精度高；其缺点是难以处理复杂外形，对一些外形上的奇点需要进行简化或特殊处理。非结构网格最早来源于固体力学中的有限元计算，主要指二维的三角形和三维的四面体网格，其优点是易于处理复杂外形，数据结构的随机性使得其易于进行网格自适应；缺点是存储量大，计算效率低。非结构网格的缺点在高雷诺数计算时表现得尤为突出：高雷诺数边界层模拟要求在物面法向有足够的网格分辨率，这一点使得非结构网格数量急剧增长。为了在一定程度上减少网格量，可以使用法向高度压缩的“各向异性”四面体单元。然而，法向相邻两个各向异性四面体单元的中心连线和物面法向的偏离使得计算在某些情况下不够精确（如利用格心型有限体积法求解单元内的物理量梯度时）。

基于结构网格和非结构网格各自的优缺点发展起来的混合网格技术结合了二者的优势：边界层内的网格一般采用半结构的三棱柱单元（在物面法向是结构的，而在贴体方向是非结构的），边界层以外单元是各向同性的四面体网格或Cartesian网格。与结构网格相比，生成复杂外形的混合网格更加容易；和纯非结构网格相比，边界层法线上有很高的网格分辨率和很好的网格正交性，又极大地减少了网格量（边界层内比非结构网格减少大约三分之二）。这无疑对提高复杂外形的数值模拟精度和效率都是非常有利的。

混合网格的出现，在提高边界层网格质量的同时，也在一定程度上缓解了生成复杂外形网格带来的困难。目前常用的三棱柱网格生成方法主要有几何层推进方法［2－3］和 求 解 双 曲 型 方 程 的 方 法［4－5］。 这 些方法在实际工程应用中得到了成功的应用。但是，对于工业应用中很多极端复杂的实际外形而言，要生成边界层的三棱柱网格并非易事，往往会在几何曲率变化剧烈的区域出现网格相交的情况，为此需要付出很多人工劳动调整局部网格分布，极大地制约了CFD的应用。

鉴于复杂外形三棱柱／四面体混合网格生成的困难，本文发展了一种自动化的基于“各向异性”四面体网格聚合的混合网格生成方法（为了叙述方便，下文称“聚合法”），即首先用已经发展成熟的非结构网格生成方法生成粘性层内的各向异性四面体单元和无粘区的各向同性四面体单元，然后将边界层内的各向异性四面体单元聚合为三棱柱，而外场的各向同性四面体单元保持不变。这种方法生成的网格在整个计算域是由四面体、三棱柱和少数多面体单元组成的混合网格。通过对DLR－F6翼身组合体和复杂战斗机外形的混合网格生成及数值模拟表明，该方法生成的混合网格具有网格质量好、自动化程度高等特点，对提高复杂外形飞行器关键气动参数的模拟精度具有重要意义。

1 非结构四面体网格生成方法简介

目前，非结构的四面体网格生成方法已经发展的比较成熟［6－7］，多种商业软件业已集成了这种方法，比如Gridgen、ICEM－CFD等。这里仅做简要介绍。非结构的四面体网格包括粘性层内的各向异性四面体网格和无粘区域的各向同性四面体网格。

生成各向异性四面体网格采用的是由阵面推进法（Advancing Front Method）改进而来的层推进法（Advancing Layer Method）。在生成好物面的三角形单元后，通过确定三角形顶点的法向和推进距离生成出拉伸的四面体单元，生成步骤如下：

（1）计算物面三角形单元顶点的推进方向。通过面积加权点p周围的面法向得到点p的推进法向，并做一定次数迭代进行光滑：

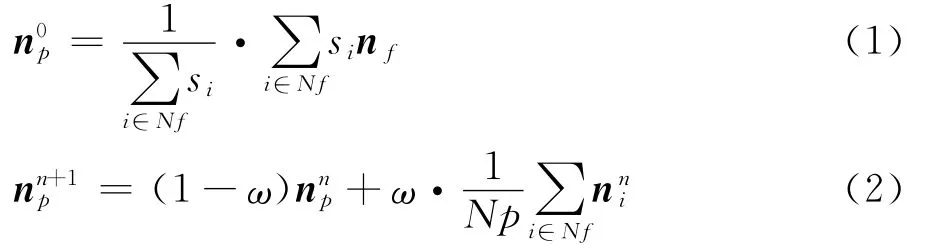
这里，Np表示点p周围的顶点数目，Nf表示和点p相连的三角形数目表示p点的法向，nf表示面的法向，n表示第n次迭代。

（2）在确定了推进方向后，需要确定推进距离，一般采用几何指数增长模式：

这里，δ0和δn分别表示第一层的网格高度和第n层的网格高度，r是法向网格距离变化率。

（3）在确定了推进方向和推进距离后，从每个顶点向计算域推出一层网格点。对于每个三角形而言，三个顶点向外推出三个点。分别将推出的三点和前一层的三个点相连，形成三个四面体单元。

在推进过程中，为了避免单元之间相交，保证交界面的相容性，需要两两判断是否相交，这在三维情况下会带来网格生成效率急剧下降。为此，可以采用“弹簧法”来判断相交性以提高效率，具体过程可参考文献［7］。

在推出给定层数的各向异性四面体网格后，停止各向异性四面体网格生成过程，形成各向异性四面体网格外边界面。各向异性四面体网格推进过程中，在局部会由于可能相交而停止推进，这些局部停止推进而形成的边界面连同其他边界面（如远场、对称面）一起，形成了各向同性四面体网格生成的初始阵面，从而进入各向同性四面体网格生成阶段。生成空间各向同性四面体单元一般采用Delaunay法或阵面推进法。在现有的商业软件中，一般将二者结合起来使用。这样既可以提高四面体网格生成效率，同时可以保证初始阵面的相容性。具体方法请参见文献［6－7］，这里不再详述。

2 基于各向异性四面体聚合的混合网格生成方法

在四面体网格生成好后，就可以用本文发展的聚合法来生成混合网格。聚合法的基本思想是，将各向异性四面体聚合为三棱柱，而各向同性四面体保持不变。这种方法一方面充分利用了非结构网格填充复杂外形计算域的自动化特点，另一方面又能聚合得到高质量的混合网格以适应粘性流动计算的需要。聚合过程主要包括四面体单元聚合、棱柱侧面聚合和边界条件处理。

2．1 四面体单元聚合

聚合四面体网格是整个算法的核心部分，其原理是充分利用层推进法生成各向异性四面体算法的特点，将三个各向异性四面体单元聚合为一个三棱柱。聚合方法直接影响到聚合后的网格质量，具体包括几个步骤：

首先，提取单元的面几何特征。对初始四面体网格，计算每个四面体的所有表面（三角形）的面积，并找出每个单元的面积最大面、次大面和最小面。

然后，根据四面体单元面的几何特征判断是否聚合，具体算法如下：

（1）根据单元的最小面和最大面的面积之比确定单元性质：

若r＜α，则该单元为各向异性，否则为各向同性。这里，Smin和Smax分别表示最小面面积和最大面面积。α是一经验参数，实践表明，α一般取值小于0．4，α取值越大则三棱柱层数越多，反之则边界层网格和无粘区域网格过渡越光滑；

（2）第一次聚合。遍历初始网格的所有面，设面Face两侧的单元分别为C1和C2，若Face是C1或者C2的最大面，并且C1或者C2是各向异性网格，则将这两个网格聚合为一个粗网格CC。定义每个粗网格里含有的子单元个数为粗网格聚合率，则CC的聚合率为2；

（3）第二次聚合。遍历初始网格的所有面，找出其两侧单元，若面Face两侧单元中有一个（C1）已被聚合而另一个（C2）尚未聚合，其中C1所在粗网格为CC，Face是C1或C2的最大面，C1或C2是各向异性单元，并且CC的聚合率小于3，则将C2聚合到CC，CC聚合率加1。

（4）第三次聚合。遍历每个尚未聚合的各向异性单元C1，找出其最大面以及最大面另一侧单元C2，和C2所对应的粗网格为CC。若CC的聚合率小于等于3，则将C1聚合到CC。

（5）遍历所有初始四面体单元Cell，若Cell尚未被聚合，则将之单独聚合为一个粗网格。

聚合过程如图1所示。第一次聚合和第二次聚合的主要目的是将三个四面体单元聚合为一个三棱柱单元。但是对于外形变化剧烈的局部网格几何特征不明显，导致其不能被聚合而成为孤立单元。如果放任之，则该单元和周围单元的体积比约为1∶3，网格过渡不光滑。为了避免网格过渡不光滑，第三次聚合将孤立单元聚合到周围的粗网格，使之和周围单元体积比约为4∶3，从而使网格光滑过渡。

图1 聚合网格过程Fig．1 Procedure of cell agglomeration

2．2 侧面的聚合

初始网格在经过聚合后形成的“三棱柱”侧面还是两个三角形。为了减少存储开销和计算量，需要将每个侧面的两个三角形合并为一个四边形，如图2。聚合面的关键在于判断哪些面需要聚合为一个面，可以通过面的左右单元属性和面法向夹角判断。值得注意的是，在合并边界面时，只有边界类型相同的两个面才能合并，比如对称面，否则会破坏几何外形和边界条件。

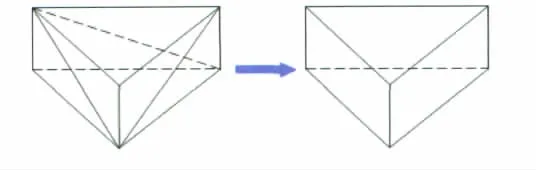
图2 合并三棱柱侧面Fig．2 Procedure of face agglomeration

边界条件的处理比较简单，将初始网格的边界条件类型直接赋予聚合后的粗网格即可。在处理好边界条件后就可以直接输出网格并进行计算。

2．3 复杂外形混合网格生成实例

为了验证本文的混合网格生成方法对复杂外形的适应性，本文首先选取了第二届AIAA CFD阻力预测会议（DPW－II）［8］中的 DLR－F6翼身组合体进行验证。如图3所示为该外形数模和局部表面网格。初始网格是全四面体网格，包括各向异性四面体网格和各向同性四面体网格，共1743万个四面体单元，3496万个面，295万个点。在聚合过程中，α取为0．4，聚合后得到781万个网格单元，2080万个面，网格单元总量减少大约一半，面的总量大约减少三分之一。如图4所示为聚合后的混合网格在x＝0．13截面和z＝0．3截面的网格视图。聚合后边界层有40层三棱柱网格，外场是四面体网格，从边界层到外场网格均匀过渡。通过聚合过程不仅网格质量得到提高，网格数量也大幅减少，计算效率也会有很大提高。

图3 DLR－F6数模和局部表面网格Fig．3 Configuration and surface grids of DLR－F6

为了说明聚合法的鲁棒性，本文生成了具有复杂外形的类F16战斗机全机外形的混合网格。如图5（a）所示为该外形的表面网格，其几何构型包括机身、机翼、平尾、立尾、腹鳍。我们采用聚合法生成该外形的混合网格量约为全场500万。图5（b）－（d）分别显示了典型截面的混合网格。通过该实例表明，聚合法有很好的鲁棒性，生成的混合网格可以保证边界层内绝大部分是三棱柱，而且从三棱柱网格光滑地过渡到外场四面体网格。

3 混合网格生成方法的应用

为了验证本文的混合网格生成方法的实用性，我们对DLR－F6（带发动机和翼吊）外形进行数值计算，并与风洞试验结果和他人计算结果进行了比较。本文采用的流场解算器是作者所在团队开发的CFD解算软件 USTAR［9－10］。USTAR 是一款基于非结构／混合网格的格心型有限体积雷诺平均N－S方程定常／非定常解算器。软件采用迎风型格式进行空间无粘项离散，粘性项采用中心格式离散。时间推进采用隐式Block LU－SGS算法［10］。为了提高计算效率，采用多重网格技术加速；对于大规模计算问题，采用了基于METIS分区的并行计算方法。软件集成了典型湍流模型，包括：一方程SA模型，二方程k－ε模型、k－ω模型和SST模型。该软件已在多种复杂外形的数值模拟中得到成功的应用。其中的具体算法请参见文献［9－10］。

计算的来流条件为DPW－II中的CASE2，即Ma＝0．75，Re＝3．0×106，攻角从－3．0°到1．5°。计算过程中采用SST湍流模型，没有考虑转捩影响。图6所示为聚合后混合网格和聚合前非结构网格的残差、俯仰力矩收敛曲线对比，可以看到混合网格不管在收敛性还是计算效率上都有很大提高。

图6 收敛历程曲线Fig．6 Convergence history

DPW会议的重点是气动力精确预测。对于气动力预测来说，网格质量尤其是边界层内网格质量的好坏直接影响到计算精度。为了验证聚合法生成的混合网格计算结果，本文不仅对比了风洞实验结果，还与DPW－II中一些参与者的计算结果进行了对比［11－14］，包 括 NASA Langley 的 USM3D 和FUN3D，Cessna的非结构解算器NSU3D和日本Kawasaki Heavy Industries的UG3。图7是聚合后的混合网格（USTAR）、聚合前的非结构四面体网格（Unstructured）、USM3D、FUN3D、NSU3D 计算结果对比。由图可见，聚合前的非结构网格计算结果和其他计算结果普遍偏差较大，证明了聚合后有效提高了网格质量。

图7（a）是计算得到的升力系数曲线。由图可见，USTAR计算结果在攻角大于0．5°时和实验结果符合较好，在攻角小于0．5°时与实验值有一定偏差，但是升力曲线和FUN3D、USM3D的结果符合较好。DPW－II会议中，大部分提交的计算结果升力曲线也符合这种趋势，即升力计算值比实验值偏大，斜率比实验值偏小［15］，这种现象在DPW－I中也普遍存在［15］。

图7（b）是升阻力极曲线。第一、二届阻力预测会议中，多数参与者提交的计算结果中阻力都比实验值偏大，如图所示，NSU3D和FUN3D的阻力都比实验值偏大，但USTAR计算的极曲线和实验值符合的较为一致。

图7（c）是俯仰力矩曲线。图中计算结果都和实验值符合的不是很理想，USTAR的俯仰力矩曲线和USM3D符合较好，处于FUN3D和NSU3D之间。和阻力预测会议收到的大部分提交结果一样，除FUN3D以外，俯仰力矩都比实验值偏大［15］。

除了气动力之外，压力分布也是本文观察的一个重点。图8是机翼沿展向不同站位处的压力分布，图中为USTAR在混合网格上的计算结果与实验值、USM3D、FUN3D的计算结果对比。在z／b＝0．150处，由于机翼上表面后缘翼身结合处分离涡的影响，计算结果和实验值都有一定偏差；在z／b＝0．331站位处，由于机翼下表面的发动机内侧有分离涡，计算结果也和实验有差异，但USTAR和USM3D明显要比FUN3D符合的好；在z／b＝0．638站位，该处外形简单流场结构单一，因此三者都和实验值均符合较好。

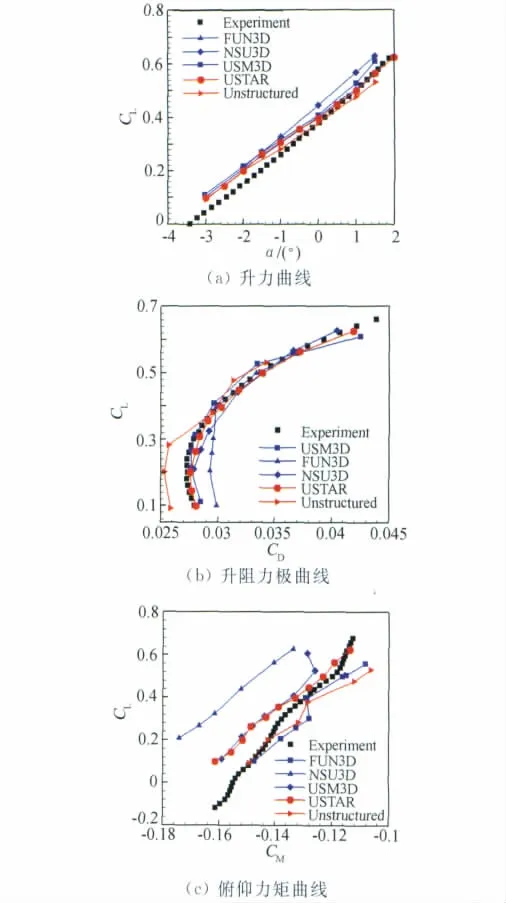
图7 DLR－F6翼身组合体气动特性计算Fig．7 Aerodynamic coefficients of DLR－F6

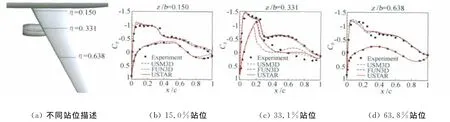
图8 机翼不同站位处压力系数分布Fig．8 Pressure coefficient distributions at z／b＝0．150，0．331，0．638

为了观察流场结构，图9画出了物面流线。图9（a）为机翼上翼面流线，图9（b）为翼身结合处流线，可看到有明显的分离现象。图9（c）为USTAR计算的下翼面发动机短舱内侧的流线，图9（d）为UG3计算结果，二者现象一致，分离区大小也差不多，但是和实验结果（图9e）相比，分离区明显偏大，在第二届阻力预测会议的总结文献里也指出大多计算结果具有分离区偏大的特点［15］。

图9 USTAR、UG3计算的物面流线和实验结果Fig．9 Streamlines over DLR－F6

4 结束语

本文针对复杂外形粘性流动网格生成费时费力的问题，发展了一种鲁棒较好、自动化程度较高的混合网格生成方法。聚合法生成的网格集成三棱柱、四面体和少数的多面体，在减少网格数量的同时提高了网格质量以增强对流场结构的捕捉能力。通过采用第二届阻力预测会议的标准算例对该方法进行了验证，结果表明该方法生成的混合网格质量适应计算的需要。通过对类F16复杂战斗机全机构型的混合网格生成，进一步说明其鲁棒性较好，表明其具有广阔的应用前景。

［1］ BAKER T J．Mesh generation：art or science［J］．Progress in Aerospace Sciences．2005，41：29－63．

［2］ PIRZADEH S．Three－dimensional unstructured viscous grids by the advancing－layers method［J］．AIAA Journal，1996，34：43－49．

［3］ KALLINDERIS Y，KHAWAJA A．Hybrid prismatic tetrahedral grid generation for complex geometries［J］．AIAA Journal，1996，34：291－298．

［4］ MATSUNO K．Hyperbolic upwind method for prismatic grid generation［R］．AIAA2000－1003，2000．

［5］ MATSUNO K．High order upwind method for hyperbolic grid generation［J］．Computers ＆ Fluids，1999，28：825－851．

［6］ LOHNER R，PARIKH P．Generation of three dimensional unstructured grids by the advancing front method［J］．Int．J．Numer．Meth．Fluids，1988，8：1135－49．

［7］ PIRZADEH S．Unstructured viscous grid generation by Advancing－Layers Method［R］．AIAA 93－3453，1993．

［8］ 2nd AIAA CFD Drag Prediction Workshop［EB］．http：／／aaac．larc．nasa．gov／tsab／cfdlarc／aiaa－dpw／，June 2003．

［9］ ZHANG L P，YANG Y J，ZHANG H X．Numerical simulations of 3Dinviscid／viscous flow fields on Cartesian／unstructured／prismatic hybrid grids［R］．In Proceedings of the 4th Asian CFD Conference［C］，Mianyang，Sichuan，China，September 2000．

［10］ZHANG L P，WANG Z J．A block LU－SGS implicit dual time－stepping algorithm for hybrid dynamic meshes［J］．Computers ＆ Fluids，2004，33：891－916．

［11］YAMAMOTO K，OCHI A．CFD sensitivity of drag prediction on DLR－F6configuration by structured method and unstructured method［R］．AIAA2004－398，2004．

［12］MAVRIPLIS D J．Drag prediction of DLR－F6using the turbulent Navier－Stokes calculations with multigrid［R］．AIAA2004－397，2004．

［13］LEE－RAUSCH E M，MAVRIPLIS D J．Transonic drag prediction on a DLR－F6transport configuration using unstructured solvers［R］．AIAA2004－554，2004．

［14］SCLAFANI A J，DEHAAN M A．OVERFLOW drag prediction for the DLR－F6transport configuration：a DPW－II case study［R］．AIAA 2004－393，2004．

［15］LAFLIN K R，BRODERSEN O．Summary of data from the second AIAA CFD Drag Prediction Workshop［R］．AIAA2004－0555，2004．