末敏子弹气动外形设计与气动特性分析
周志超,赵润祥,韩子鹏,陶 钢
(南京理工大学 能源与动力工程学院,江苏 南京 210094)
0 引 言
末敏弹是当今世界各国弹药发展的主要方向之一,其末敏子弹的探测器要对地面目标进行搜索扫描,发现和识别目标后射出爆炸成型弹攻击装甲目标的顶部,而稳态扫描技术是末敏子弹的关键技术之一[1]。我国当前已定型和正在研制的末敏子弹都是利用旋转降落伞形成子弹的稳态扫描,而无伞扫描是利用末敏子弹的气动力和质量分布不对称形成的,因而末敏子弹气动外形设计、气动力计算方法研究和气动特性分析成为实现无伞扫描运动的前提。
要实现末敏子弹的无伞扫描,必须在气动外形上满足以下条件:为子弹提供平衡系统重量、达到一定落速的阻力;产生稳态扫描所需的滚转力矩,维持必要的转速;提供俯仰力矩、偏航力矩等,使子弹的平均扫描角保持稳定。
末敏子弹的弹体通常采用短圆柱体,因为短圆柱体能够多枚装填于母弹之中,且具有较大的阻力。然而,短圆柱体的阻力仍不能平衡弹重,静稳定性也无法保证子弹在平均扫描角下稳定,且无法产生滚转力矩。因此,必须设计尾翼,使末敏子弹的气动外形满足战技指标要求。
本文从末敏子弹气动外形的战技指标出发,以钝头短圆柱为弹体,设计了一种轴向折叠尾翼气动外动外形进行了风洞测力实验和数值模拟,对外形气动力、计算区域流场及弹体表面压力分布进行分析。
1 气动外形和布局设计
弹体采用了如图1的外形,长细比λ≈1.2,头部为钝头,后部无船尾,整个弹体母线不连续。通过设计合理的尾翼外形和布局,为子弹提供足够的阻力,保证弹体在轴对称平面内稳定,并产生滚转力矩使子弹绕弹轴匀速旋转。
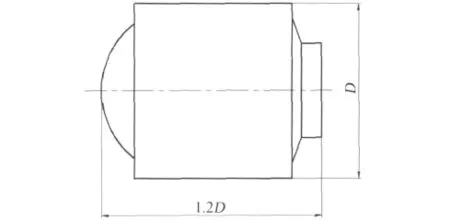
图1 弹体外形图Fig.1 Shape of the projectile
图2 为尾翼弦向和展向尺寸示意图,凹面圆弧的曲率半径为Rw,对应的弦长bw,圆弧圆心角φw,外露翼展长为lw。尾翼的外露面积为Sw,其表达式为:
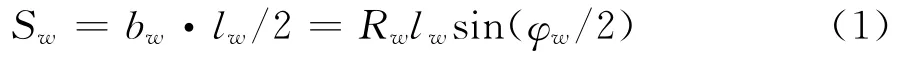

图2 尾翼尺寸示意图Fig.2 Dimension of tail fins
由于弹径和翼厚度一定,尾翼合拢后需贴于弹身侧面,因此凹面圆弧曲率半径Rw是确定的。由式(1)可以看出,尾翼的外露面积Sw与圆心角φw和外露翼展长lw有关。尾翼的外露面积直接决定了尾翼的迎风面积,迎风面积越大,尾翼产生的阻力也就越大。
图3为外形轴向视图,毛弹翼展长lw′由弹体直径D、翼根到弹身的垂直距离ldw和外露尾翼翼展lw决定:

毛弹翼展长的不同,决定了尾翼伸出弹体的距离,它能影响气流在尾翼上的流动,导致阻力产生变化。
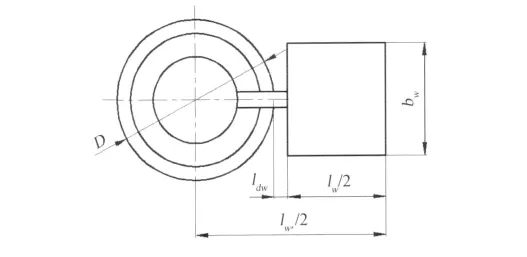
图3 外形轴向视图Fig.3 Axial view of the shape
如图4,翼剖面与迎角平面平行,当翼剖面对称线与弹轴夹角为0°时,翼弦与弹轴垂直,相当于尾翼对弹轴的安装角δ=90°。尾翼上下剖面圆弧圆心角各为φw/2。翼剖面中心与翼剖面圆弧圆心都位于弹轴平面内。当来流迎角α=0°时,翼上下表面的流动是对称的,则气流在翼表面的压力分布亦上下对称,此时翼的法向力为零,不产生滚转力矩。
为使子弹绕弹轴获得一定的滚转力矩,可以将尾翼进行偏转。图5为将尾翼绕翼剖面中心进行偏转的示意图。将尾翼以剖面圆弧圆心偏转角度δa时,翼剖面对称线与弹轴产生大小为δa的夹角,尾翼的安装角变为δ=90°-δa。假设偏转角为顺时针方向夹角,此时翼上剖面与弹轴夹角减少δa,下剖面与弹轴夹角增加δa,翼剖面中心离开弹轴平面,翼上下剖面在弹轴平面两侧不对称。
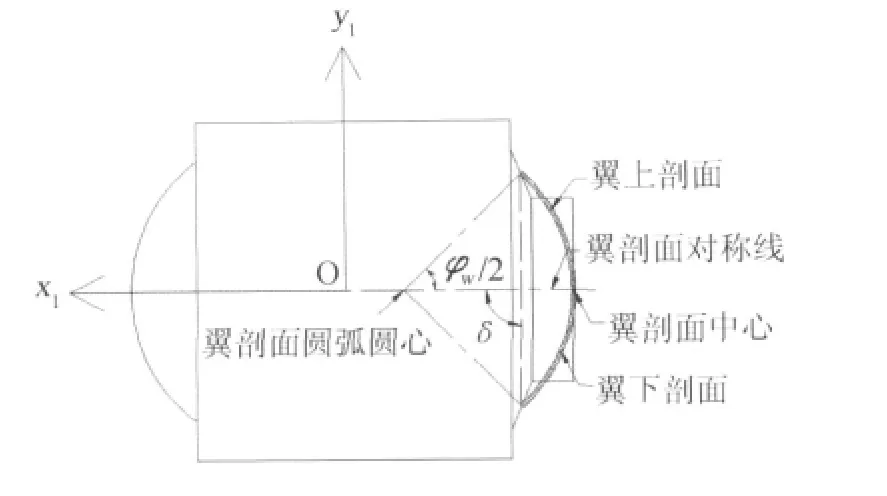
图4 尾翼无偏转侧视图Fig.4 Side view of the fin without deflecting
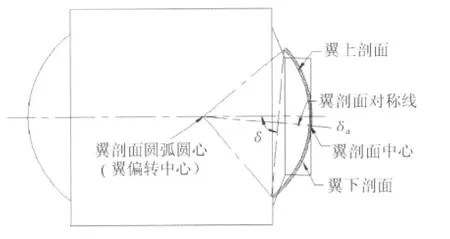
图5 尾翼偏转示意图Fig.5 Side view of the fin with deflecting
当尾翼发生偏转时,如果来流迎角α=0°,翼上下表面产生的气动力在y1轴方向就不会完全抵消,这样尾翼就会产生法向力,当单片翼安装角或者多片翼偏转角δa相同时,尾翼就会产生滚转力矩,从而推动弹体绕弹轴旋转。
当偏转角度为δa时,翼外露面积在子弹轴向和法向的投影面积分别为:
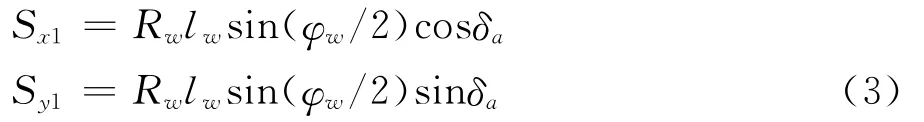
由式(3)可以看出,当弹径和翼厚度一定时,尾翼凹面圆弧的曲率半径Rw为定值,则尾翼在弹体轴向和法向的投影面积,与翼展、翼剖面圆弧圆心角和偏转角有关。翼展、剖面圆弧圆心角越大,尾翼在两个方向上的投影面积越大;尾翼偏转角越大,在弹体轴向的投影面积越小,在弹体法向的投影面积越大。尾翼在弹体法向的投影面积越大,法向力也就越大,滚转力矩也随之增大。
由于单片翼无法使弹体保持稳定,因此在保证不过多增加尾翼数量的情况下,可以通过翼的对称布局使弹保持稳定,如图6。翼的对称布局是指翼的展、弦长以及偏转角度相同,周向均匀布局。在尾翼数量上,有三片翼、四片翼和六片翼等基本布局,实际尾翼数量不能过多。尾翼布局示意图如图7(a)~(c)所示。

图6 多片轴向折叠尾翼布局Fig.6 Distribution of multi-axial-folded fins
确定了尾翼数量Nw和尾翼布局方式后,就可以得到尾翼最大弦长bwmax、最大外露面积Swmax和最大总外露面积STwmax的表达式:
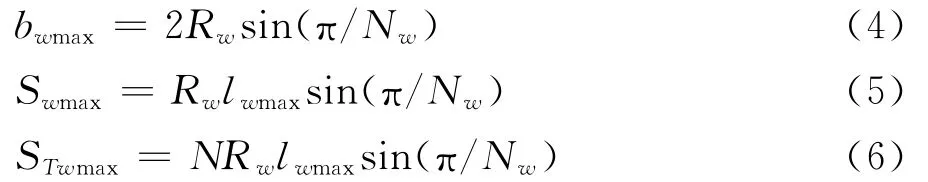
从式(4)~式(6)可以看出,尾翼数量越多,可以取到的尾翼弦长越短,外露面积越少,但总的外露面积越大。

图7 轴向折叠翼布局示意图Fig.7 Sketch map of distribution of axial-folded fins
2 数值模拟方法
2.1 控制方程
控制方程采用积分形式的无量纲化预处理雷诺平均N-S方程:
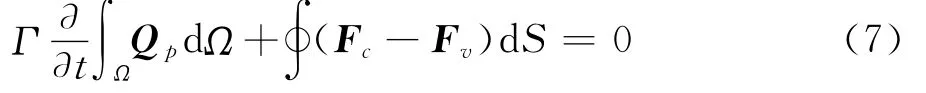
式中:Qp为原始解向量;Fc和Fv分别为对流和粘性矢通量;Γ为预处理矩阵。具体表达形式参见文献[2]。
2.2 离散方法
采用格心格式的有限体积法,在结构网格下将式(7)半离散化可以得到
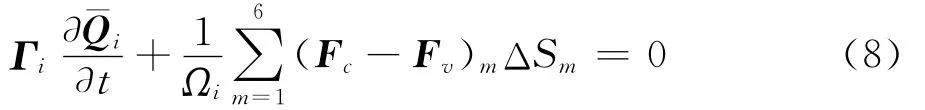
采用二阶线性重构方法计算控制面m的左右解向量QL和QR:

式中:di,m为控制体i中心到控制面m 中心的距离;φ为限制器函数,采用van Albada限制器。δ+,δ-分别为前插和后插梯度算子:
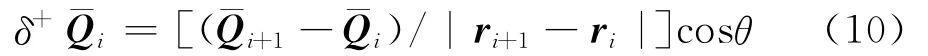
式中:θ为向量(ri+1-ri)和(ri-rm)的夹角。
在式(9)获得控制面重构变量的基础上对矢通量进行离散,其中对流项采用预处理的AUSM+-up格式[3]。AUSM+-up格式的关键是引入了压力耗散项Mp和速度耗散项pu:

式中:fa为预处理项,fa=Mr(2-Mr)。为了使时间推进和空间的预处理参数统一,本文取M2r=β。AUSM+-up格式的其他参数定义见文献[3]。预处理参数β采用Turkel[4]提出的全局截断法,并且考虑了当地粘性因素影响。
控制面粘性通量Fv,m采用全粘性通量,其中的一阶导数采用奥高公式求解。采用层流模型作为湍流封闭求解N-S方程,其中动力粘性系数μ采用Sutherland公式计算。时间方向采用预处理的LU-SGS隐式时间推进方法[5]。
2.3 边界条件
物面边界条件采用无滑移条件;远场条件采用Turkel[6]提出的简化的远场边界条件。
3 气动特性分析
为研究无伞末敏子弹的气动特性,进行了风洞实验和数值模拟。风洞实验模型采用了三片尾翼气动外形,实验结果及分析在文献[7]中给出。计算外形与实验模型外形相同,生成的网格如图8所示,其中图8(a)和图8(b)为流场网格截面示意图,图8(c)为弹表面网格图。计算了来流V∞=50m/s,迎角α=-10°~10°状态下的流场和气动力。
3.1 气动力计算结果分析
图9(a)为阻力系数随迎角变化曲线。从图中可以看出,阻力系数在3.0以上,达到了增阻效果。计算结果与实验结果相比较,阻力系数在α=-2°~8°时基本吻合,在α=-8°~-4°时计算值大于实验值。

图8 流场及弹表面网格Fig.8 Mesh of the flow filed and projectile
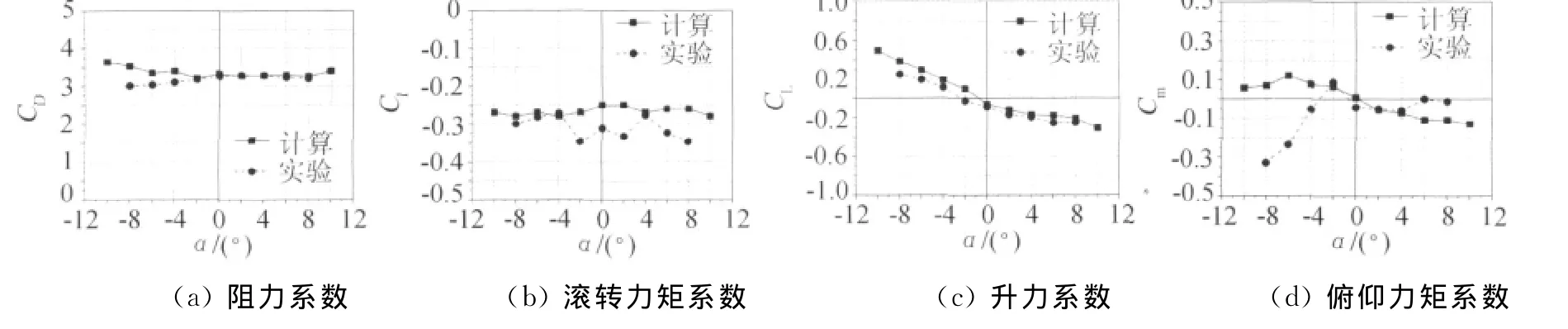
图9 实验和计算的气动力系数Fig.9 Experimental &computational aerodynamic force coefficients
图9 (b)为滚转力矩系数随迎角变化曲线。从图中可以看出,计算的滚转力矩系数比实验值略大,随迎角变化不大。
图9(c)为升力系数随迎角变化曲线。计算结果与实验结果变化趋势相同,均随迎角增大而减小,并且,在负迎角下系数基本为正,在正迎角下系数全部为负。
图9(d)为俯仰力矩系数随迎角变化曲线。在α=-2°~4°时,计算值与实验值基本吻合。在α=-8°~-4°偏差较大:计算值为正,随迎角增大系数值先增大后减小,实验值为负,随迎角增大而增大。在α=6°~8°时,计算值与实验值也略有差异。
3.2 流场计算结果分析
图10(a~f)分别为V∞=50m/s,α=-8°~8°状态下,迎角平面内的流场等压线和流线图。在α=-8°时,气流在弹头部形成高压,过弹头部在弹身两侧形成低压。气流在上侧尾翼迎风面形成高压,过尾翼翼梢产生膨胀,压力降低。由于迎角平面的下侧没有尾翼,因此,气流在整个弹身下表面的压力较低。随着迎角的增大,弹头部的高压区范围变化不大。弹身上表面低压区范围随着迎角的增大而扩大,与之相对应的是,尾翼迎风面的高压区随着迎角的增大而缩小。
从图10(b)可以看出,在α=-8°时,气流在弹头部产生驻点并分离,向头部两侧流动,并在弹身两侧形成涡,其中上表面的涡更靠近弹头部。在上侧尾翼迎风面靠近翼梢处,气流产生驻点并分离,一部分气流向翼梢流动,一部分向翼根流动,并在尾翼与弹底部的凹槽形成涡。气流在翼梢分离并拖出尾迹向远场延伸,与底部的回流气流交汇产生涡。尾翼背风面也有涡产生。气流过弹头下侧肩部发生分离,其它区域的气流补充到弹身下表面,形成涡。随着迎角的增大,弹头部驻点的位置变化不大。弹身上表面涡的范围随着迎角的增大而增大,到α=8°时,涡覆盖了尾翼迎风面的大部分区域。随着迎角的增大,气流过弹头肩部在弹身下表面分离的程度逐渐降低,弹身下表面的涡有所减小,到α=8°时,气流只在下表面靠近头部的地方形成一个小涡。

图10 V∞=50m/s不同迎角下迎角平面压力和流线图Fig.10 Pressure contours and streamlines at different angles of attack at V∞=50m/s
3.3 圆柱部压力系数分析
图11 (a~c)分别为V∞=50m/s,α=-8°,0°和8°弹表面压力等值线图,可以看出,圆柱部表面的压力分布是比较复杂的。如图11(a),在弹身上取轴向I、轴向II和轴向III三条母线,其中轴向I母线为y轴正向尾翼连接杆对称平面内的圆柱部母线,轴向II母线为z轴正向尾翼连接杆对称平面内的圆柱部母线,轴向III母线为迎角平面内y轴负方向的圆柱部母线。
由图12(a~c)对比可以看出,弹身沿轴向的压力变化,不仅与迎角有关,与尾翼的存在也有很大关系。在α<0°时,弹在纵向低头,对于轴向I来说,由于尾翼的影响,压力沿轴向的分布先低后高,且高压区比较靠近弹尾部,位于弹的质心位置之后,这样,可以起到使弹抬头的作用;而在α>0°时,弹在纵向抬头,压力沿轴向的分布趋于平缓,因此其对稳定性影响减弱。对于轴向II来说,无论迎角正负如何,沿轴向II的压力系数均为先高后低分布,在α<0°时,弹在纵向低头,这样一种压力分布,会起到削弱稳定性的作用,而在α>0°时,弹在纵向抬头,这样一种压力分布,会起到增强稳定性的作用。相比较而言,轴向III由于没有尾翼与之直接对应,因此压力系数随迎角的变化没有轴向I和轴向II明显,对弹稳定性的影响没有轴向I和轴向II明显。

图11 V∞=50m/s不同迎角弹表面压力等值线图Fig.11 Pressure contours of projectile surface at different angles of attack at V∞=50m/s

图12 弹表面压力系数分布Fig.12 Pressure coefficients of projectile surface
3.4 尾翼压力系数分析
图13 (a~c)为不同迎角下,弹头部和尾翼迎风面压力等值线图。尾翼A、B、C选取如图13(a)所示。从图中可以看出,在α=-8°时,翼根和翼梢附近的压力较低,翼面中部的压力较高,其中尾翼A的高压区范围较大,尾翼B和C的高压区略靠近翼梢,且翼根的低压区范围较大。α=0°时,各翼面的压力分布较为一致。α=8°时,尾翼A大部分为低压区,只在翼梢附近有高压区存在,尾翼B和C的高压区范围没有明显扩大。
图14(a~c)分别为不同尾翼迎风面的压力系数沿展向的分布曲线,尾翼沿展向的压力系数取自连接杆对称面内的尾翼迎风面。当α>0°时,尾翼A沿展向靠近翼根的大部分迎风面的压力系数降低,而尾翼B和尾翼C的压力系数变化不大,由于在α>0°时,尾翼A产生的俯仰力矩将使弹进一步抬头,而尾翼B和尾翼C产生的俯仰力矩将使弹低头,因此这样一种压力变化将增强弹的稳定性。当α<0°时,尾翼A沿展向的压力变化不大,而尾翼B和尾翼C的压力在α=-8°时才明显减小,因此在α<0°时尾翼产生的稳定力矩不如α>0°时的大。
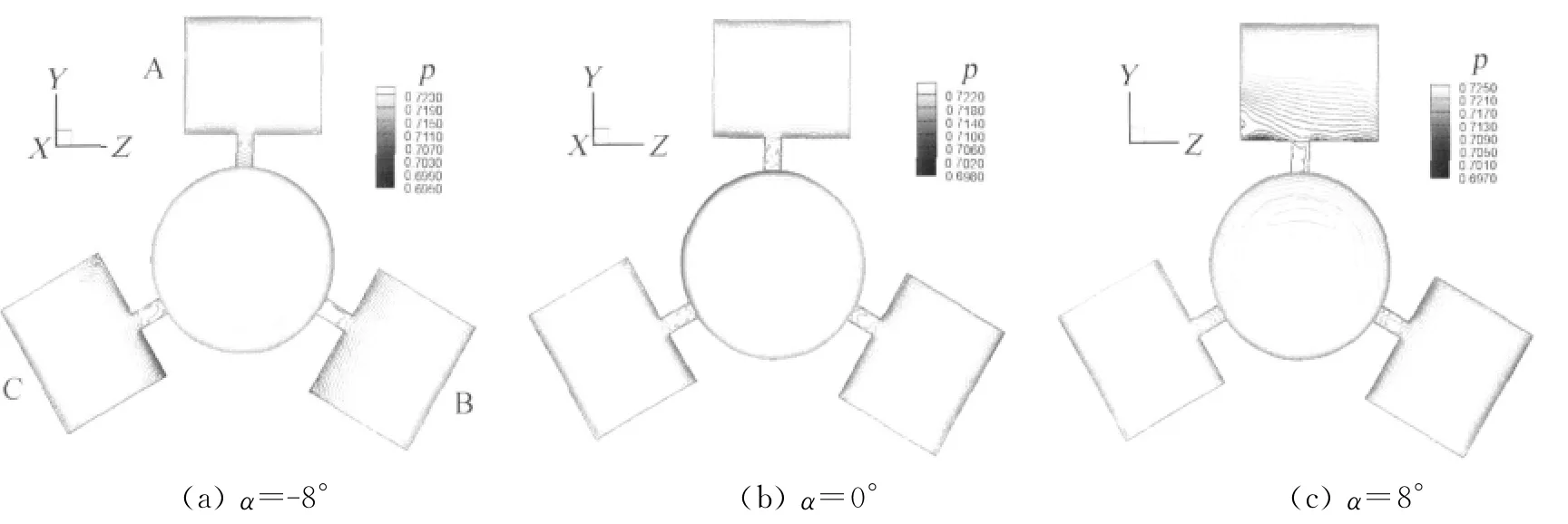
图13 V∞=50m/s迎风表面等压线图Fig.13 Pressure contours of windward surface at V∞=50m/s
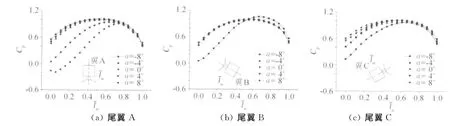
图14 尾翼迎风面展向压力系数分布Fig.14 Pressure coefficients of windward along span
4 结 论
本文给出了一种轴向折叠尾翼末敏子弹的气动外形设计方法,采用了风洞实验和数值模拟方法对三片尾翼的气动外形进行了气动特性分析。阻力与升力系数的计算结果与实验结果吻合较好,而俯仰力矩系数和滚转力矩系数有所差异。流场计算结果显示:流场随迎角的变化很大,且翼体干扰严重。尾翼的存在提高了圆柱部、尤其是圆柱部尾部的压力,从而增强了弹体的静稳定性。弹体的存在降低了整个尾翼迎风面,尤其是翼根部的压力。其一方面削弱了尾翼的增阻效果,但另一方面增强了尾翼的静稳定性。而三片翼特殊的尾翼布局方式,使得α<0°时,弹身和尾翼产生的稳定力矩不如α>0°时的大。本文的气动外形设计方法和气动力计算结果可为该类型末敏子弹的设计提供参考。
[1] 韩子鹏等.弹箭外弹道学[M].北京:北京理工大学出版社,2008.(HANG Zi-Peng,etc.The exterior ballistics of projectiles[M].Beijing:Beijing Institute of Technology Press,2008.)
[2] JESPERSEN D,PULLIAM T,BUNING P.Recent enhancements to overflow[R].AIAA paper 97-0644,1997.
[3] LIOU M S.A sequel to AUSM,Part II:AUSM+-up for all speeds[J].Journal of Compuattional Physics,2006,214:127-170.
[4] TURKEL E.Preconditioning techniques in computational fluid dynamics[J].Annual Reviews of Fluid Mechanics,1999,31:385-426.
[5] DAILEY L D,PLETCHER R H.Evaluation of multigrid acceleration for preconditioned time-accurate Navier-Stokes algorithms [R]. AIAA paper 95-1668-CP,1995.
[6] TURKEL E,RADESPIEL R,KROLL N.Assessment of preconditioning methods for multidimen sional aerodynamics[J].Computers &Fluids,1997,26:613-634.
[7] 周志超,赵润祥.不同尾翼灵巧子弹气动特性实验研究[J].实验流体力学,2010,24(4):52-55.(ZHOU Zhi-Chao,ZHAO Run-Xiang.Experimental investigation on aerodynamic characteristic of smart submunitions with different tail fins[J].Journal of experiments in fluid mechanics,2010,24(4):52-55.)

