注水井悬浮微粒侵入伤害模拟研究

朱红旺，周泓宇，李年银，赵立强 （西南石油大学石油工程学院，四川成都610500）

陈平 （中石油吐哈油田分公司鄯善采油厂，新疆 鄯善838202）

在注水过程中注入率的下降是广泛存在的。一个重要的原因是，注入流体中的固体微粒被岩石所捕集，这导致了渗透率的下降和注水井的欠注。为了更高效地开发油田，对伤害程度及范围进行模拟，用以指导解堵措施是非常有必要的。

将试井得到的表皮因数进行分解[1]，结合经典Hawkins公式对伤害半径进行预估，以及使用改进的麦金利图版[2]进行预测，都得到了很好的应用效果。由于条件限制，对于多井次的解堵施工设计有较大的难度。

考虑临界流速在伤害半径预测[3]中的应用，模型计算简便，使用参数较少，不能很好地反映油田注水实际情况，且用岩心对临界流速测试的实验条件要求严格，容易产生较大误差，从而影响模拟结果。

Liu等[4，5]建立的由于注入悬浮微粒导致注水井堵塞的数学模型，是建立在多孔介质中微粒运移模型[6]之上的。Liu和Civan[4]所建立的两相流微粒运移模型，考虑了注入流体中微粒的润湿性差异，以及其在孔隙表面的沉积，在孔隙喉道的捕集和在油水两相间的传递。针对具体的实例，实验得到了描述各种微观机理的经验常数，应用模型模拟计算得到了很好的拟合结果。模型尽可能地描述了各种微观伤害机理，但该模型所需参数较多，由于实验条件所限，每个参数不易取得，所以其应用也受到限制。

Moghadasi等[7]应用Matlab程序的Simulink软件，基于多孔介质中的质量守恒，对由固相侵入造成的地层伤害进行了模拟。Zuluaga等[8]应用人工神经网络和模糊模型，对微粒侵入造成的地层伤害进行了仿真模拟，尝试用一种新的数学方法来解释微粒侵入地层所造成的伤害。Shi[9]以PFC3D商业软件为建模基础对固相微粒侵入造成伤害进行了模拟。

综上所述，以往应用的预测模型分为两类，一类为宏观伤害模型[1～3]，计算简便，能得到伤害程度和范围的解析解，但并没有考虑特定地层性质的微观机理，不能很好地反映地层实际情况。另一类为微观伤害模型[4～9]，在充分考虑了微粒及地层的特殊性质情况下，其中经验参数的测试由于设备限制比较困难；利用神经网络学习模拟过程需要足够多的样本，对于缺少多井次资料的情况来说具有局限性；利用大型商业软件3D建模是近年来国外对注水井伤害进行评估的主要手段。

笔者根据深床过滤理论中微粒的捕集机理，考虑岩石对微粒的最大捕集量不仅与自身的孔隙结构有关，也与微粒的粒径分布相关，选用较易由流动实验取得的能反映地层水和地层实际情况的经验参数，根据经典渗滤模型 （对流方程），且为了避免直接数值求解过程中出现非物理现象振荡，对模型进行半解析求解。

1 微粒捕集机理

仅考虑注入水中所携带的外源微粒对油层所造成的伤害。一旦微粒被孔隙介质中流动的流体所携带，则考虑以下3种影响其运移的主要机理：①扩散——孔隙内存在悬浮物微粒浓度梯度，使得微粒被孔隙表面所捕获的机理即属于扩散作用，主要发生在小于1μm的微粒中；②沉积——当微粒物距离孔隙表面很近时，且水流速度很小，将会有由重力产生的沉积作用，3～30μm的微粒中沉积作用较为显著；③水动力——孔隙介质中的流动通道极不规则，当悬浮物微粒沿弯曲的流线运动时，流速的大小和方向发生突变，微粒由于惯性与孔隙表面接触而被捕获，对1～3μm的微粒影响较大。图1为注入水中微粒捕集示意图。

油田注入水中悬浮微粒在多孔介质中的运移与被捕集过程，和水处理过程的过滤理论[6]较为相似。在20世纪30年代末，日本Tominisa Iwasaki（岩崎）根据长期对过滤过程的研究，发表了下列关系式[10]：

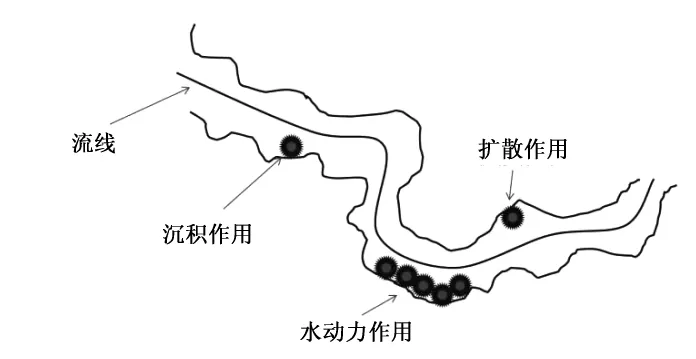
图1 注入水中微粒捕集示意图

式中：N为滤层深x处单位时间内的面积微粒浓度，微粒数/（cm2·d）；λ为过滤系数，与滤料粒径、滤速和微粒相关；λ0为清洁地层的过滤系数；ε为常数，与滤料粒径、滤速和微粒相关；σ为沉积量，微粒数/cm3。

可以由在滤料粒径、滤速和微粒材料3个参数的各种组合条件下进行试验，分别获得相应的过滤系数λ和常数ε的数值。

从20世纪50年代中期的以后20多年内，出现了大量的过滤理论的文献。其中具有代表意义的，是来自前苏联的ΜИΗЦ和英国的Ives发表的论文引起的争议，但他们仍有以下共识：①每个薄滤层内所去除的微粒物量和进入这个层的微粒物浓度成正比；②滤池的过滤行为，从冲洗后进行过滤起，是随时间变化的；③每个滤层从进水中所去除的悬浮微粒物量和滤层中所累积的微粒物量相等；④每个滤池最终将达到一个饱和的阶段，不再具有去除悬浮微粒物的能力；⑤滤池进口处的第1个滤层首先达到饱和阶段，然后沿水流方向逐渐传到其他滤层。

但ΜИΗЦ认为在整个过滤过程中，包括饱和阶段在内，微粒沉积在滤料上的速率为常数，且已沉积在滤料上的微粒将会以正比于沉积量的速率脱落下来。而Ives则认为，过滤行为的变化只表现为悬浮微粒沉积在滤料上的速率，先递增后递减，在饱和阶段为零。考虑到油藏中多孔介质较给水处理中所用滤料更为复杂，弯角处由因水动力作用而被捕获的微粒填充，改善了多孔介质的流动条件，使得流线趋于平缓，从而减小了由于水动力等作用造成的微粒捕集的情况应该更为显著。笔者采用Ives的假设，微粒在沉积到最大值后，将不会再发生沉积。

以前的模拟研究中，将整个多孔介质中微粒的最大捕集量作为一个常量进行处理。笔者认为在近井地带，由于孔喉的曲折，且对注入水粒度分析得到的注入水中值粒径为2.5μm，这些微粒更容易受到水动力作用的影响，率先被多孔介质所捕获。这点也能被近井地带渗透率的较快下降所印证。所以，经由悬浮物微粒质量浓度测定所得到的最大捕集量，在径向距离上不应该为一常量，应该为近井地带的最大捕集量较大，且由油藏的具体情况所决定的，在确定时间下对不同长度岩心进行流动实验后得到以下关系式：

式中：σmax为最大沉积量，mg/cm3；x为长度，cm；a1、a2为采用现场岩心进行流动驱替试验所得经验参数，求取过程将在后面阐述。

2 模型建立

2.1 假设条件

建立模型所做的假设条件为：①流体不可压缩；②由岩石捕获的微粒并不会造成 “水－微粒”系统体积的变化。

2.2 多孔介质中悬浮和滞留微粒守恒方程

式中：c为悬浮微粒浓度，mg/cm3；t为时间，s；q为注入流量，cm3/s；r为半径，cm；h为注水层位厚度，cm；σ为 沉积量，mg/cm3。

经典渗滤理论认为滞留速率与流体流速和悬浮微粒浓度c成比例，且与沉积量σ相关的比例系数λ被称为渗滤函数λ（σ）。

假设捕集速率与已捕集微粒总量成反比，得到滞留速率动力学方程：

比较式（6）、（7）可得：

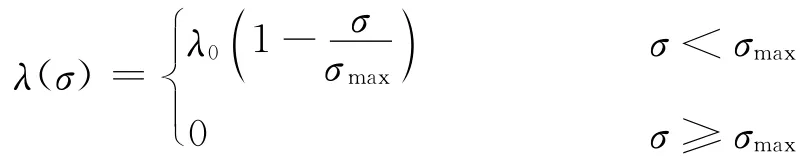
其中，σmax为最大沉积量，其沿径向分布为σmax＝－a1lnx＋a2，当σ超过σmax时，微粒将不再在孔隙中沉积。λ0和σmax，都将由岩心流动试验测得。

微粒的滞留导致了岩石渗透率的减小，这个过程与σ相关，得到以下方程：

一般，得到一个关于K（σ）的函数表达式，其中p为注入压力，MPa；K、K0分别为地层渗透率和地层初始渗透率，mD；β为地层伤害系数，β2为第二地层伤害系数，为了拟合试验数据，更常用的形式为β2非零。方程（8）描述了地层伤害系数β与滞留微粒浓度σ的线性相关。值得注意的是，β和β2的取值不仅与地层性质相关，与注入流体的性质也相关。

式（5）、（6）含有c和σ两个未知数，可由以下初边值条件进行求解。

式中：c0为注入水中初始悬浮微粒浓度，mg/cm3；rw为井筒半径，cm。

为了计算的简便和可靠性，引入无量纲距离X、时间tD、悬浮微粒浓度C、沉积量S、无量纲压力pD及渗滤函数无量纲化Λ（S）。

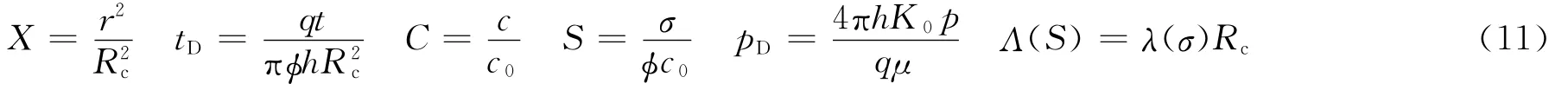
式中：φ为地层孔隙度，1；Rc为供给半径，cm，大小为注水井与采油井距离的一半。线性坐标X与径向无量纲半径的平方相等。

将无量纲化后各参数代入悬浮微粒运移、滞留守恒方程（5）、（6）及渗透率损伤方程 （8），得：

即有无量纲化初始、边界条件：

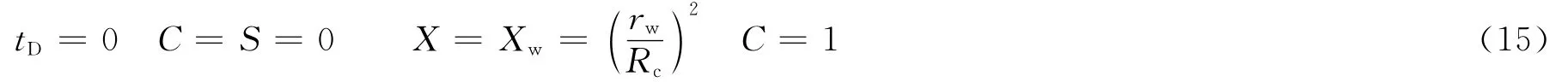
2.3 径向渗滤的半解析模型

为了进行半解析求解，首先引入势的概念：

代入式（12）、（13），并利用初始、边界条件式（15），可化简得：

由此可以看出，Φ（S）的引入，使得偏微分方程的阶数降低。

结合方程（16），将方程（17）进行微分，得

得到的一阶双曲线方程（18）可用特征线法求解，其特征方程如下：

在考虑线性渗滤系数和变化的岩石最大捕集量下，由特征曲线方程（19）可得方程的柯西条件，方程（20）可写为如下形式：

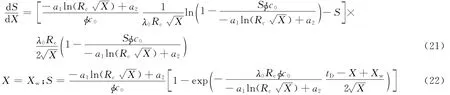
综上，可以由方程（21）和边界条件（22）对近井地带的悬浮微粒浓度沿径向分布进行求解，进而求得渗透率损害，对地层伤害程度和范围进行评估。

3 模型经验参数试验获取

由于在岩心流动试验中，微粒沉积的数据并不是均匀的，所以不能由试验结果直接得出经验参数，需要由试验数据反演。

注入水采用油田实际注入水样，定注入速度，考虑渗滤和地层伤害系数为常数，各参数见图2岩心流动试验示意图。

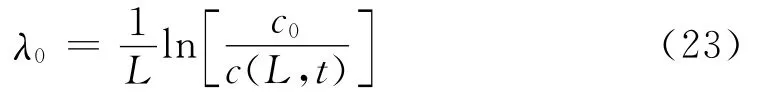
式中：c（L，t）为长度为L的岩心在t时刻流出流体中的悬浮微粒浓度，mg/cm3；L为岩心长度，cm。

定义无量纲压力降为阻抗系数，有

式中：Δp（t）为t时刻流动压差，MPa；m为常数系数。

由某一时刻流动压差可计算出m值，且地层伤害系数β可由下式得到：

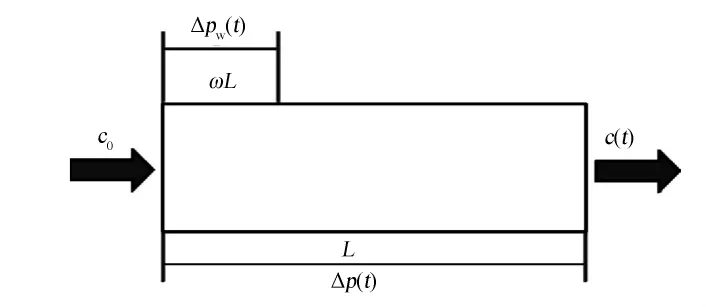
图2 试验参数示意图

微粒最大沉积浓度σm沿径向分布，可以由定注入水微粒浓度与不同长度岩心流动实验结果拟合得到经验常数a1、a2。

4 实例计算分析

方程 （22）及其边界条件 （23），可由四阶龙格库塔法求解计算。解得的无量纲数据进行回代参数，可得伤害半径与微粒沉积浓度分布、渗透率分布关系。笔者采用Matlab进行了编程模拟计算。基础参数见表1，模拟结果见图3～6。

表1 模拟计算基础参数表

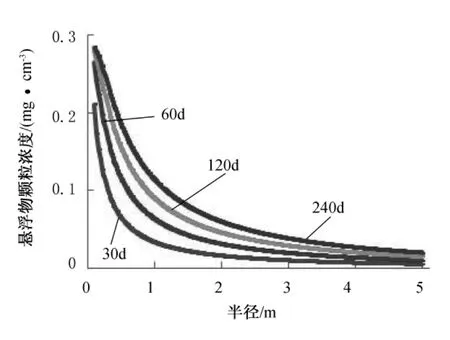
图3 固相微粒沉积浓度分布与时间、距离的关系

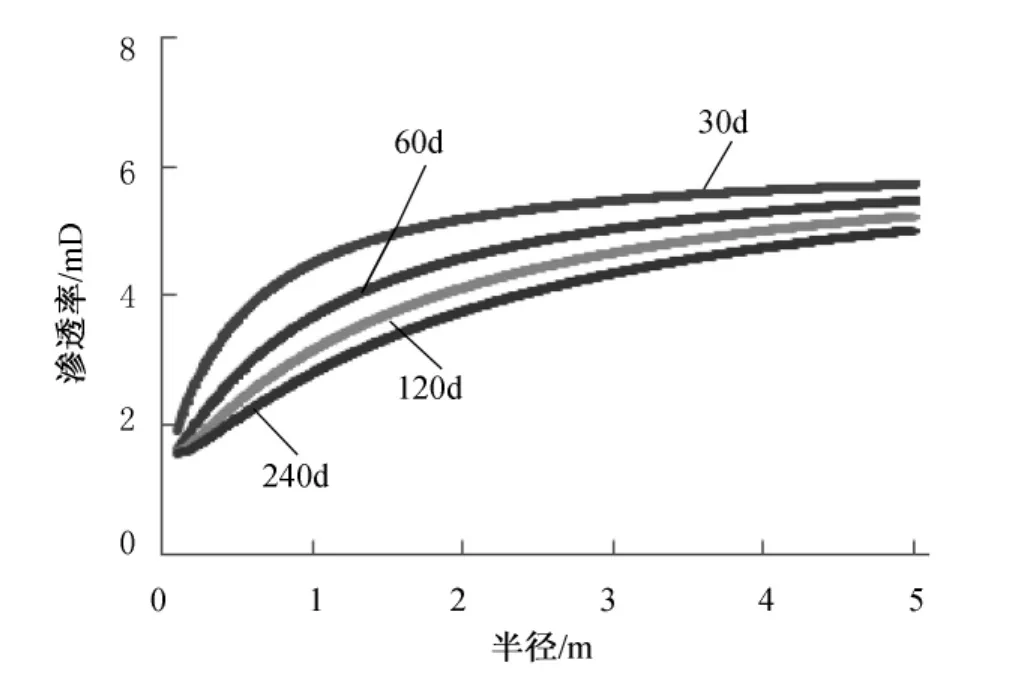
图4 近井地带渗透率分布与时间、距离的关系

由模拟计算可看出，在现场注入水悬浮微粒浓度为0.29mg/cm3时，井筒处渗透率下降73.33%，且距井筒1m处渗透率下降55%，2m处渗透率下降30%，由此推断悬浮微粒造成的主要伤害半径在1～2m之间，近井地带的污染较远井处更为严重，随着注入时间的增加，伤害向地层深部推进。当注入水中悬浮微粒浓度相差3倍时，在近井地带对地层渗透率的伤害可达2倍之多。所以在注水过程中，控制悬浮微粒浓度尤为重要。

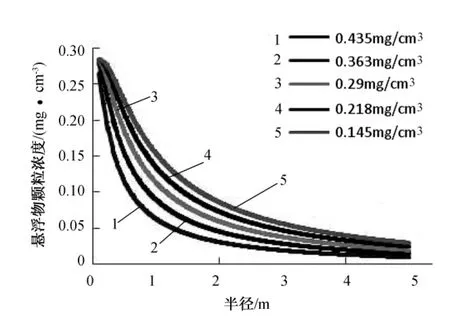
图5 不同微粒注入浓度对固相微粒沉积分布影响

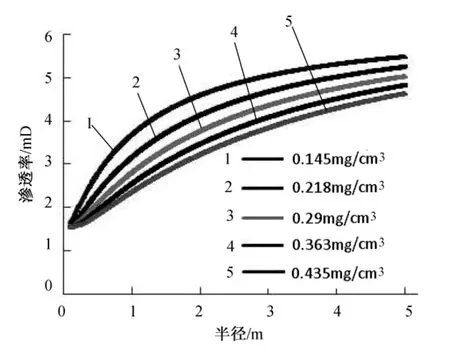
图6 不同微粒注入浓度对渗透率分布影响

5 结论

1）笔者认为由于注入悬浮微粒粒径分布的差异，其所受岩石捕集的机会存在大小。在近井地带岩石能捕集更多的较大悬浮微粒，流入地层深部的较小微粒被捕获的几率较小。这使得在某一时刻近井地带的岩石最大捕集量较地层深部大。且随着注入总量的增加，远井处的最大捕集量也会逐渐增加。

2）应用半解析模型对悬浮微粒侵入进行模拟，所得结果虽然显示悬浮微粒侵入了地层深部，但其主要在近井地带1～2m产生严重影响。

3）由实验测得的参数，对模拟结果影响较大，测试过程要严格控制实验条件，尽量排除干扰，方能测得较为精确的值。

[1]刘建军，闫建钊，程林松 .表皮因数分解与油气层伤害定量评价 [J].油气井测试，2005，14（2）：17～19.

[2]霍进，陈陆建，王本成，等 .储层伤害试井评价新方法研究 [J].西南石油大学学报，2012，34（1）：108～113.

[3]罗明亮，蒲春生，樊友宏 .储集层微粒运移堵塞预测模型及其应用 [J].油气地质与采收率，2001，8（3）：74～76.

[4]Liu Xinghui，Civan Faruk.Formation damage and skin factor due to filter cake formation and fines migration in the near－wellbore region [J].SPE27364，1994.

[5]Liu X.Modeling of formation damage due to particulate processes in linear and radial two－phase flow system [D].Oklahoma：The U－niversity of Oklahoma，1994.

[6]法鲁克·西维 .油层伤害——原理、模拟、评价和防治 [M].北京：石油工业出版社，2003.

[7]Moghadasi J，Sharif A，Kalantari－Dahaghi A M，et al.A new model to describe formation damage during particle movement and deposition in porous media [J].SPE99391，2006.

[8]Zuluaga E，Alvarez H D，Velasquez J D.Prediction of permeability reduction by external particle invasion using artificial neural networks and fuzzy models[A].Canadian International Petroleum Conference [C].Calgary，Alberta：2000－06－04～08.

[9]Shi Xiaoyan.Permeability estimation of damaged formations near wellbore [J].SPE146833，2011.

[10]Iwasaki T，Slade J J，Stanley W E.Some notes on sand filtration[with discussion][J].Journal（American Water Works Association），1937，29 （10）：1591～1602.