基于滑模控制的三相四线制有源滤波器的研究

吴雷，周怡

（江南大学 江苏 无锡 214122）

随着科学技术的迅猛发展，电力电子技术变得更加成熟，各种大功率开关器件得到了广泛的应用。技术的发展虽然给电能的变换应用带来了很大的方便，但是也造成了严重的电力系统谐波污染[1]。有源电力滤波器是一种功能强大的电力电子装置，它对谐波能快速跟踪同时实现谐波和无功功率的补偿。

在我国的电力系统中，工厂和居民用电一般采用三相四线制的形式接入。以往的研究主要集中于三相三线制系统，所设计的有源电力滤波器并不适用于三相四线制系统。三相四线制系统往往与不平衡负载相连接，中线电流不为零。系统中不仅有谐波正序分量，还有负序分量和零序分量。由于以上因素，设计三相四线制系统中的有源滤波器的难度较大。有源电力滤波器的主电路为变流器，变流器的控制策略在很大程度上影响了有源电力滤波器的补偿性能。常见的有源滤波器控制策略有电流滞环控制、三角波比较控制、无差拍控制和电压空间矢量控制等，在应用中都有一定的局限性。分析有源电力滤波器的主电路可知，它工作在不同的开关模态下，是一个变结构控制系统。滑模控制具有很强的鲁棒性，对于外界干扰表现自适应性，适合作为变结构非线性系统的控制策略[2]。因此，本文将滑模控制理论应用于有源电力滤波器的电流跟踪控制中。

1 三相四线制有源电力滤波器主电路数学模型

文中主电路变流器的拓扑结构采用三相四桥臂拓扑结构，如图1所示。其中，桥臂的输出电感用L来表示，开关器件用T1~T8来表示，直流侧电容用C来表示，三相输出电流用ifa、ifb、ifc来表示，直流侧电流用 idc来表示，中线电流用 ifn来表示，电网电压分别用Usa，Usb，Usc来表示，各个桥臂的中点相对于直流母线负端 N 点的电位分别由 Ua，Ub，Uc，Un来表示，直流母线电压由Udc来表示。

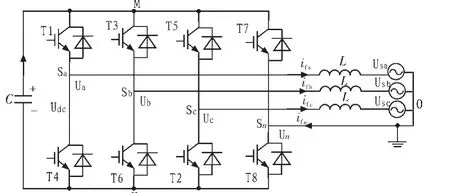
图1 四桥臂变流器主电路拓扑结构Fig.1 Topology structure of main circuit with four bridge inverter

开关函数Si定义为如下：

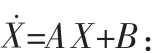
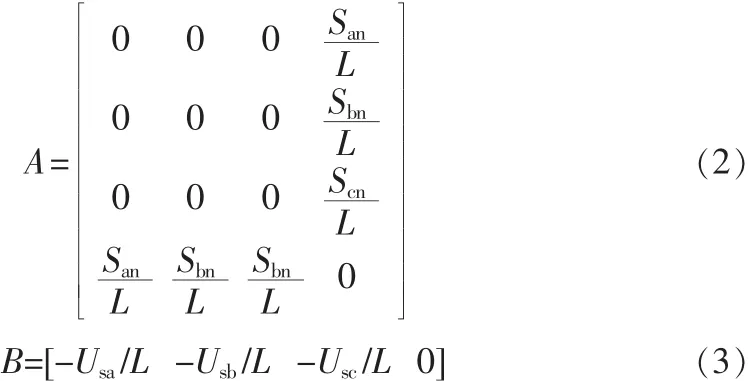
其中，Ua_ref=Ua-Un，Ub_ref=Ub-Un，Uc_ref=Uc-Un。 另外，令 San=Sa-Sn，Sbn=Sb-Sn，Scn=Sc-Sn，同时引入状态变量 X，X=[ifaifbifcifn]T将abc坐标系转换到dq0同步坐标系，以方便设计控制器。考虑到坐标变换在实际系统中关联到锁相，本文锁相信号由正弦A相相电压来表示，同时根据正弦制作坐标变换的表，变换矩阵和Park变换的变换矩阵稍有差别，如式（4）所示：

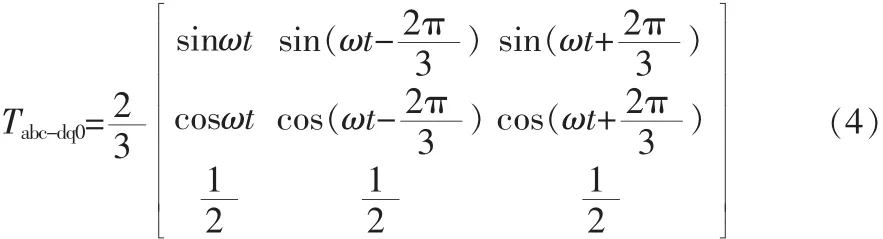
得出d-q-0坐标下的数学模型：

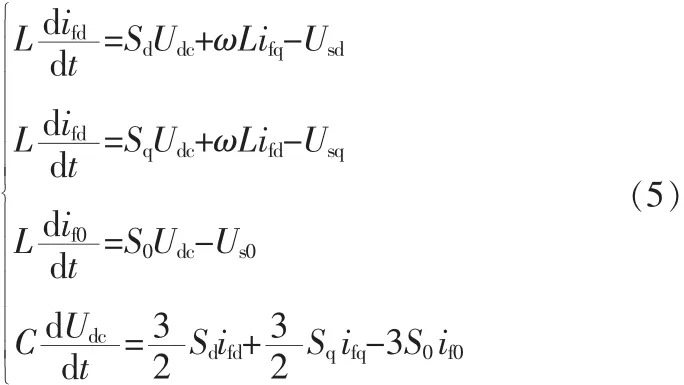
由式（5）可知，同步旋转坐标变换的时候引入d、q轴之间的耦合项。当电流控制器采取闭环调节的时候，d轴或者q轴的输出电流通常会受到彼此控制量的影响，这将会对控制系统产生严重的影响，在设计控制器时需要先进行解耦的处理。

2 逆系统解耦线性化

逆系统方法的基本原理[3]可概括为:原系统和原系统的α阶可逆系统之间带有一个状态反馈，这个状态反馈是根据原系统的初始值和α阶可逆系统的初始值之间的关系设定的α。阶可逆系统逆系统和原系统串联起来之后得到伪线性系统。得到伪线性系统后，一般将该系统分成几个独立的子线性系统，再分别设计控制器。可见，通过逆系统将原本的非线性系统转化为了伪线性系统，使问题得以简化，降低了控制器设计的难度。

在上文中已经推导出了三相四桥臂有源电力滤波器在d-q-0 坐标下的变量表示。 在式（5）中，令[x1，x2，x3，x4]=[ifd，ifq，if0，Udc]，[u1，u2，u3]=[Sd，Sq，S0]，[y1，y2，y3]=[x1，x2，x3]，将原系统的状态方程写作：

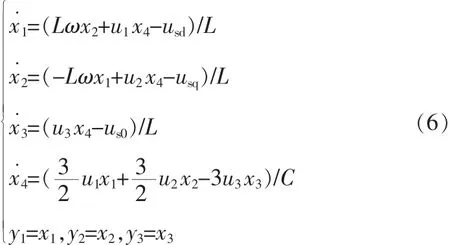
由式（6）可知，三相四桥臂有源电力滤波器系统具有3个输入[x1，x2，x3]和 3 个输出[y1，y2，y3]，具有非线性特征，且变量之间存在耦合的关系。将被控对象进行逆系统构造，得到一个线性解耦的系统，利于控制器的设计[4]。

对 APF 的系统输出[y1，y2，y3]分别求导可得：

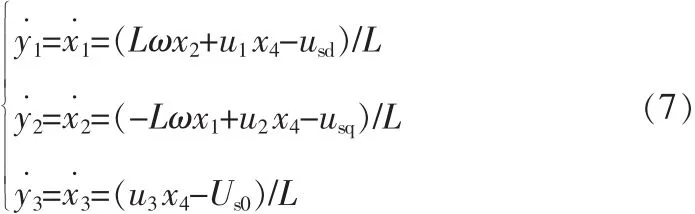
式中可明显看出含有[u1，u2，u3]，由式（7）可求得有源电力滤波器的逆系统如下:

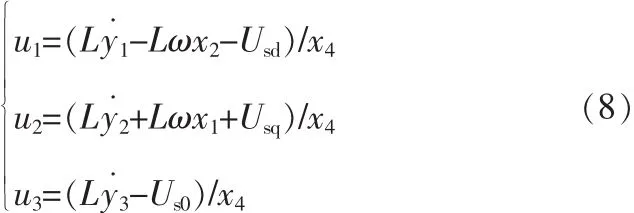
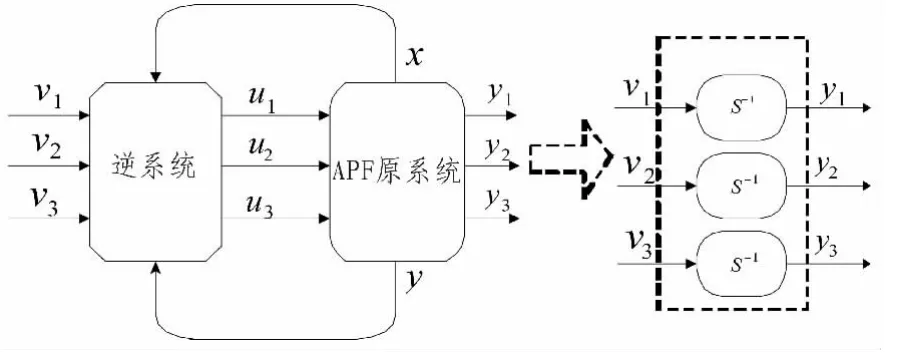
图2 线性化解耦后的有源电力滤波器系统Fig.2 Active power filter system after linearization and decoupling

图2中的伪线性具有三输入和三输出，状态变量之间彼此不存在耦合，可以看成3个独立的子线性系统：

3 滑模控制器的设计

本文设计的滑模控制器必须保证能实现对指令电流的快速、精确跟踪。此外，由于电网的不稳定和负载的突变，补偿电流也是不断变化的，这就要求系统具有良好的鲁棒性。众所周知，滑模控制的鲁棒性非常优良，所以控制器的设计重点应该解决合适的切换面和性能优良的控制律。

1）切换面的选择

2）滑模控制律的设计

该部分即确定系统在趋近运动段的运动状态，选取指数趋近规律进行设计，如式（12）所示：

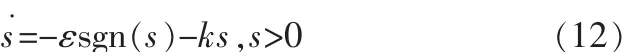
指数趋近律中的-ks部分称作指数趋近项，-εsgn（s）部分称作等速趋近项[5]。考虑将等速趋近变为变速趋近，变速趋近项为-εs2sgn（s），变速趋近的速度与s2成正比。当运动点远离滑模面时趋近速度很大，运动到滑模面附近时，速度较小，改进后的指数趋近律如式（13）所示：

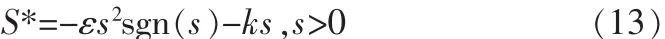
下面检验改进后的指数趋近律是否满足滑动模态存在和可达条件：

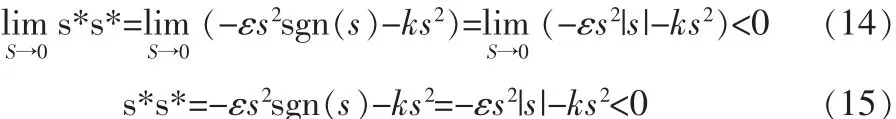
以上分析可知，改进后的指数趋近律可以满足条件。

为了更近一步减小抖振，考虑用饱和函数代替式（13）中的符号函数。饱和函数图像如图3所示。

图3 饱和函数图像Fig.3 Image of saturated function

饱和函数的公式表达如式（16）所示：

符号函数具有继电器特性，开关切换会造成系统控制的不连续性。用饱和函数代替符号函数，在[-φ，φ]的区间内采用线性控制而不是变结构控制。饱和函数的边界层附近增益高，并有一定量的时间滞后，可以缓和开关切换的不连续性[6]。本文采用指数趋近律与饱和函数切换相结合的方法设计滑模趋近律，大大减弱了抖振，同时也能保证快速趋近，使控制器具有更好的动态性能。

式（9）所示子系统经过改进滑模控制律分别为：

按照同样的方法设计式（10）和式（11）所示的子系统的控制律：

取趋近律函数的参数 k1=k2=k3=105，ε1=ε2=ε3=1。

4 仿真分析

搭建好系统仿真模块之后，进行仿真来验证本文理论的正确性。仿真时间为0.2 s，在0.04 s向系统中投入有源滤波器，负载为三相整流桥。

当三相整流桥谐波源负载工作时，向电网注入大量5次和7次谐波，负载侧电流发生畸变，成为鞍形波，此时，电源侧电流也是鞍形波。经0.04 s时，有源滤波器投入，电网侧畸变为鞍形波的电流恢复为正弦波，谐波被滤除，如图4所示。

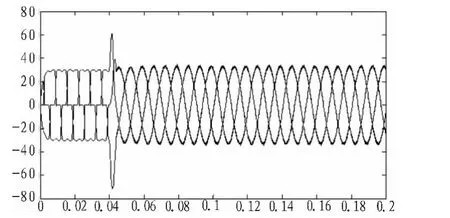
图4 电网侧电流Fig.4 Grid-side current

在没有投切有源滤波器的时候，对电网谐波电流进行FFT分析。补偿前的谐波畸变率THD=24.66%，电网被严重污染，如图5所示。

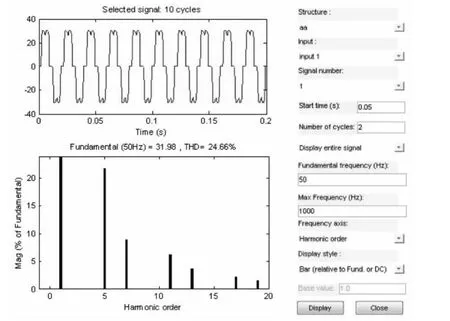
图5 补偿前电网侧电流的FFT分析Fig.5 FFT analysis of grid-side current before the compensation

采用滑模控制，补偿后的谐波畸变率THD=0.60%。由此可见，采用滑模控制能让有源滤波器具有良好的补偿效果，如图6所示。

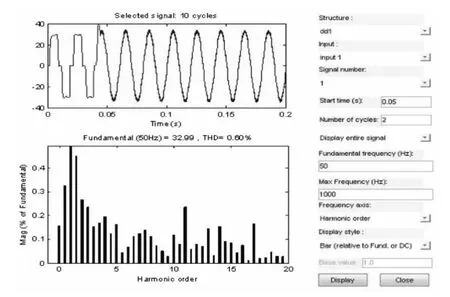
图6 补偿后电网侧电流的FFT分析Fig.6 FFT analysis of grid-side current after the compensation

5 结 论

基于三相四线制有源滤波器的主电路的数学模型，用逆系统方法实现解耦和线性化，对三个独立的子系统分别设计滑模控制器。针对滑模控制的抖振问题，提出一种指数趋近律结合饱和函数的设计方法，缓解结构切换的不连续性，有效削弱抖振。仿真结果证明，本方法适于有源滤波器的工作特点，能提高有源电力滤波器的指令电流跟踪能力，同时系统具有强鲁棒性。本方法具有较好的理论和实用价值，为工程实践提供了新的思路。

[1]Ying Jie-he，Yunping Zou，Fei Liuet al.Research on parallel operation of active power filters[C]//IEEE Power Electronics Specialists Conference，2006.18-22.

[2]马皓，张涛，韩思亮.新型逆变器滑模控制方案研究[J].电工技术学报，2005，20（7）:50-56.

MA Hao，ZHANG Tao，HAN Si-liang.Analysis and design of sliding mode control for novel buck inverter[J].Transactions of China Electrotechnical Society，2005，20（7）:50-56.

[3]李泰，王奔.基于逆系统方法的三相PWM整流器直接功率控制[J].电气传动，2008，38（10）:33-38.

LI Tai，WANG Ben.Direct power control of three phase PWM rectifier based on the inverse system theory[J].Electric Drive，2008，38（10）:33-38.

[4]魏文辉，刘文华，宋强，等.基于逆系统方法有功无功解耦PWM控制的链式STATCOM动态控制策略研究[J].中国电机工程学报，2005，25（3）：23-28.

WEI Wen-hui，LIU Wen-hua，SONG Qiang，et al.Research on fast dynamic control of static synchronous compensator using cascade multilevel inverters[J].Proceedings of the CSEE，2005，25（3）:23-28.

[5]Cortes D，Alvarez J，Vazquez N.Output Feedback Sliding-Mode Control for the Boost Inverter[C]//Proceedings.of IEEE IECON’06.Paris:2006：1890-1895.

[6]金鸿章，罗延明，肖真，等.抑制滑模抖振的新型饱和函数法研究[J].哈尔滨工程大学学报，2007，28（3）:288-291.

JIN Hong-zhang，LUO Yan-ming，XIAO Zhen，et al.Investigation of a novel method of saturation function for chattering reduction of sliding mode control[J].Journal of Harbin Engineering University，2007，28（3）:288-291.