叶片吸力侧反曲率设计对流道内激波强度影响的研究

王宇峰，温风波，王松涛，陈绍文(哈尔滨工业大学 发动机气体动力研究中心，黑龙江 哈尔滨 150001)

0 前言

现代高性能燃气轮机的负荷较高，在涡轮高压级流道内会出现局部超音速流动，因而会在叶片尾缘产生强激波，带来较大的激波损失。激波与附面层相互影响，会导致附面层增厚，也是气动损失升高的重要原因之一。Doorly［1］等学者通过实验手段研究了尾迹和激波对下游跨音速动叶的影响，观测到并记录了复杂的激波反射。王凯［2］通过数值计算得出，激波可以在吸力面反射点局部产生较强的逆压梯度，会导致附面层提前分离，气动损失增加。此外，激波也是发动机噪音的重要来源之一［3］，控制激波强度能够有效地减少航空发动机的噪音，对于战机的隐身性能有所帮助。张少波、庞可等学者的研究发现，在蒸汽轮机的叶栅以及抽气阀门结构中，控制激波强度也是十分必要的。钟兢军等学者的研究发现，合理控制激波强度是保证高超声速进气道性能的关键。王扬平等［4］在对超燃冲压发动机的研究中发现，斜激波可使入射点及下游附近的冷却效率下降20%，同时也发现这种影响不会向上游传播。激波后流体静压增加、马赫数降低，总温提高，冷却效果降低。雷雨冰等［5］做了超声速流中激波与湍流附面层相互作用的数值模拟。研究发现，气体经过激波后，压力突然上升，对附面层内的亚声速区域产生作用，导致附面层局部区域压力升高，干扰强烈时附面层发生分离。减小涡轮流道内逆压段长度能够抑制叶片表面附面层增厚，从而降低叶型摩擦损失［6］。张立刚［7］、Leiss［8］、孙奇［9］等学者的研究表明，前加载叶型控制二次流动的能力稍弱，但前加载、均匀加载负荷分配方式更有利于适应较大的负荷。

本文详细研究了某型航空发动机高压涡轮第一级导向叶片流道内的激波结构及其随出口马赫数变化的规律，以及叶型吸力侧反曲率设计对控制激波强度、减少叶型损失的效果，为超音速叶型的设计提供参考。

1 计算域实体建模及网格划分

1.1 二维计算域实体建模

涡轮叶片的实体为1 mm厚的薄片。为了观察整个流场的发展过程，计算域流道长度应足够长，但不宜过长。为保证计算域的长度，计算域进口段为流场参数均匀区域，计算域出口段长度为尾缘后流向距离一个弦长。流体域采用结构化网格，叶片表面为O形网格，其余部分为H形网格，网格总数约为12万。近壁第一层网格厚度为0.05 mm，增长率为1.1。采用ANSYS软件包中的ICEM CFD网格划分软件建立计算域网格。使用软件中的Quality标准进行衡量，整个计算域网格质量全部在0.1以上。为避免数值震荡，在叶高方向划分两层网格。如网格图1所示。

1.2 湍流模型和边界条件选取

该叶型设计点进口总压2.12 MPa，总温1 650 K，出口静压0.88 MPa，通过改变背压来实现不同出口马赫数的工况，并以此研究超声速流动条件下叶型的气动性能。不同工况下叶栅出口马赫数与叶栅出口背压的对应关系如表1所示。计算采用ANSYS 12.1软件包中的CFX求解器，选择标准k－ε湍流模型，采用高精度混合离散格式进行求解。时间步长为自动控制，步长因子选为0.3。

图1 原型叶片二维计算域网格

表1 不同工况下叶栅出口马赫数

1.3 改型设计方案

在对原型叶片进行改型设计的过程中应用叶型的36参数造型方法进行几何造型［10－13］，提出四种造型方案。改型设计时变动了λm、λ2以及吸力侧后半段NURB曲线控制参数。其中λm为最大厚度方向角，即叶片最大厚度的切线方向相对于叶弦的方向角;λ2为尾缘角，即叶片的出口几何角与安装角之差;吸力侧后半段NURB曲线控制参数如图2所示。其中h、g为距离，w为权重。

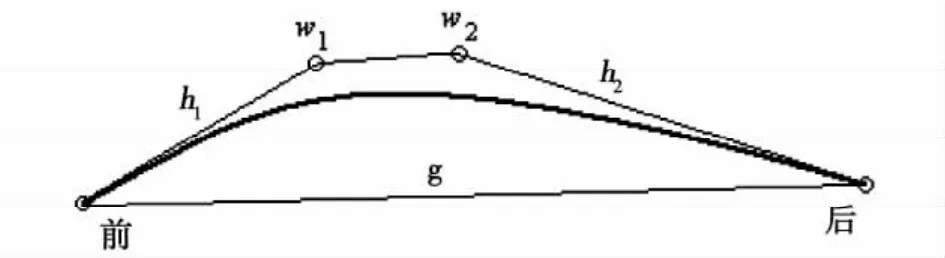
图2 叶型36参数造型方法NURB曲线控制参数示意图

表2为原型、改型设计方案相关参数对比。结合图2可见，各改型方案均减小了叶型后缘角，将吸力侧后段NURB曲线的第二个控制点置于吸力侧型线内部。同时加大了两个控制点距离前、后切点的距离，又便于型线的拉伸。增加第二个控制点的权重可以便于反曲率造型。图3为各方案的叶型对比，可以看出，改型叶片吸力侧的反曲率造型，其曲率开始变为负值的位置、反曲率程度、反曲率区域长度均有不同。图4为局部吸力侧型线曲率随相对弧长变化关系。从上述各图中可以看出，方案1中的叶型反曲率区域长度适中，曲率变负位置相对最接近尾缘，反曲率程度适中;方案2中的叶型反曲率区域较长，其曲率变负位置相对较接近前缘，并且其反曲率的程度较大;方案3中的叶型曲率变负位置基本与方案2叶型一致，但反曲率区域长度最长、反曲率程度最大;方案4的叶型反曲率区域最短，曲率变负位置相对最接近前缘，并且反曲率程度最小。

图3 二维叶型的四种改型方案对比

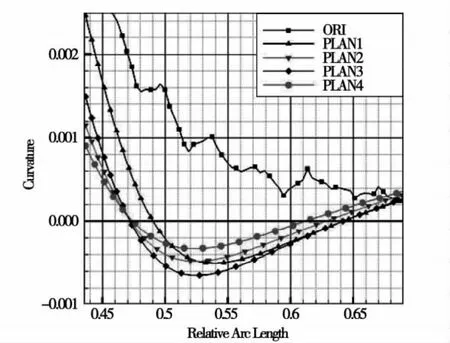
图4 二维叶型的四种改型方案曲率随相对弧长变化

表2 改型设计方案变动参数描述

2 计算结果分析

将上述所示的四种改型方案分别造型，进行数值模拟，并与原型叶型对比分析了气动性能的变化。

2.1 改型叶片绝对马赫数分析

出口马赫数为1.7(工况1)、1.2(工况2)两个工况下的原型以及各个改型方案的流道中马赫数等值线分别如图5、图6示。图中两横线区域为原型及各改型方案中，激波在叶型吸力侧上的反射点变化区间。通过流道中马赫数的变化以及等值线的疏密程度可以对不同方案中流道内激波强度进行分析。

图5 出口马赫数为1.7工况下各方案流道内马赫数等值线

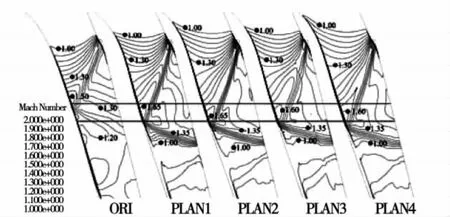
图6 出口马赫数为1.2工况下各方案流道内马赫数等值线

由图5可以看出，在出口马赫数为1.7的工况下，改型方案的激波反射点相对于原型方案向后移动，并且方案4中的反射点最贴近尾缘，减少了吸力侧逆压段长度。同时，改型方案相对于原型方案也减小了流道中最大马赫数的大小，一定程度上减弱了激波强度。当叶栅出口马赫数为1.3时，扩压段长度的减小就已经十分不明显了，此时方案1、方案2并不能减小激波强度，反而流道中最大马赫数还有所升高。方案3、方案4中的最大马赫数稍有下降，但是激波附近高马赫数区域比原型叶片稍大。当叶栅出口马赫数继续降低至1.2时，如图6所示，虽然激波反射点仍有一定后移，但是改型方案中的激波强度均比原型方案中的激波强度有所增加。并且相对于原型方案，流道中均产生了较强的反射激波，增加了能量损失。

2.2 叶片表面静压分析

图7、图8、图9为不同改型方案进行计算后得出叶片表面的静压分布与原型的对比。从上述图中可以看出，在叶栅出口马赫数为1.3、0.8的工况下(背压为 0.40 MPa、0.68 MPa)，如图 7、图 8 所示，流道中激波强度很大，改型方案的吸力侧最低压力点比原型方案的最低压力点的压力值要高，所以损失下降。根据能量守恒方程，最低压力降低，流体流动速度提高，进而导致摩擦损失的增加，即叶型损失增加;壁面处流动速度接近于0，压力基本接近于滞止压力，最低静压值提高证明总压损失的减小。从图7中可以看出，在这个工况点下，吸力侧激波后的扩压段长度也有所变化。改型方案中的吸力侧扩压段的长度均比原型方案的扩压段长度要短。在高马赫数工况下，方案4的叶型减少扩压段的效果尤其明显。扩压段长度越小，则逆压流动区域越小，对吸力侧该区域的附面层增厚的抑制作用越强，越能够减小叶型摩擦损失。

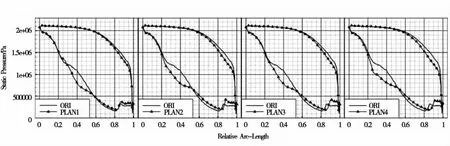
图7 出口马赫数为1.7工况下各方案叶片表面静压分布

图8 出口马赫数为1.3工况下各方案叶片表面静压分布

图9 出口马赫数为0.8工况下各方案叶片表面静压分布

当叶栅出口马赫数在0.8及以下时，如图9所示，改型叶片相对于原型叶片吸力侧出现一个低压区，并且压力侧尾缘附近压力会低于吸力侧压力。这是因为吸力侧反曲率设计使得流道由一个渐缩喷管变为一个拉阀尔喷管。在亚声速流动情况下，气体在通过喷管喉部之后压力升高，使得改型叶型流道中出现低压区。低压区的存在会导致叶型损失的增加。这说明，吸力侧反曲率叶型不适用于亚声速流动。

从图中还可以看出，吸力侧逆压段的压力升高程度各不相同。从图中可以看出，在高马赫数工况下，激波后的压力升高的程度比原型叶片稍有减小;在马赫数较低的工况下，逆压梯度反而有所升高。改型叶型在控制激波强度方面的性能比原型叶型有所提高，但在低马赫数工况下反而有所下降。这也说明，虽然反曲率叶型对于高马赫数下的流动适应性较好，但并不适用于亚声速流动情况。在马赫数较高的工况下，方案4的叶型在控制激波强度方面要略强于原型。

改型方案同样改变了叶片的负荷分配。原型叶片为后加载叶型，在各改型方案中，叶片最大负荷位置均向前移动至中部附近，使得原后加载叶型变为前部或均匀加载叶型。这样的前加载、均匀加载负荷分配方式更有利于适应较大的负荷，在高负荷、高出口马赫数叶型上有着较高的气动性能。

3 结论

本文对流道中含有激波的二维叶型进行了CFD数值模拟，并对叶型进行了反曲率改型设计。通过对改型方案的数值模拟以及对压力、马赫数等指标的分析，发现在高马赫数工况下，反曲率叶型具有如下的特点:

(1)在控制激波强度方面，采用叶型后半段较薄、且曲率变负的位置较接近前缘的设计(如方案3、方案4)能够在降低流道中最大马赫数以及激波前后马赫数差异上表现较好。但方案3和方案4的高马赫数区域略宽。由此可见，在激波强度较大的情况下，曲率变负位置接近前缘且尾缘附近较薄的叶型能够带来较为理想的性能;

(2)从激波与附面层相互作用角度来看，方案3和方案4的设计有利于减小高马赫数流动工况下的扩压段长度，从而减小附面层增厚的区域。同时，方案3与方案4的设计也能减小流道中的激波强度。这样，同时减小激波与附面层两方面的损失，在激波与附面层相互作用时，会降低损失。不同的是，方案4在高马赫数条件下的气动性能较方案3略优。即曲率变负位置在一定程度上越靠近前缘，其高速条件下性能越好。

综上，尾缘附近较薄的反曲率叶型对控制叶栅中的超声速流动较为合适，并且随着马赫数升高，曲率开始变负的位置也应逐渐向前移动，可以达到保证叶型在超声速情况下的综合性能的目的。

［1］D.J.Doorly and M.L.G.Oldfield.Simulation of the Effects of Shock Wave Passing on a Turbine Rotor Blade.ASME Journal of Engineering for Gas Turbines and Power.1985，107(4):998－100.

［2］王凯.跨声速高压气冷涡轮机气动性能研究［D］.哈尔滨:哈尔滨工业大学，2009.

［3］王凯，王松涛，王仲奇.冷气喷射法控制激波强度的数值研究［J］.航空动力学报，2010.25(6):1374 －1380.

［4］张少波.冷凝机组供热改造中汽轮机内效率的提高［J］.节能技术，2001，19(3):34 －36.

［5］庞可，潘诚.汽轮机速关阀不同开度下的流动特性数值研究［J］.节能技术，2011，29(4):301 －305.

［6］钟兢军，严红明.高超声速二维前体/进气道一体化优化设计研究［J］.节能技术，2006，24(4):303 －307.

［7］王扬平，姜培学.超音速气膜冷却及其受斜激波的影响［J］.工程热物理学报，2007.28(1):137 －139.

［8］雷雨冰，梁德旺，黄国平.超声速流中激波/湍流附面层干扰数值模拟［J］.南京航空航天大学学报，2004.36(1):1－5.

［9］王仲奇，秦仁.透平机械原理［M］.北京:机械工业出版社，1988:79－85.

［10］张利刚，韩万今.后部加载叶型的气动优化设计［J］.节能技术，2004.22(1):15 －16.

［11］C.Liess，P.Weiss and L.Fottner.The Influence of Load Distribution on Secondary Flow in Straight Turbine Cascades［C］.ASME Journal of Turbomachinery.1985，117(3):732－735.

［12］袁峰，张才稳，黄海舟，等.尾迹对涡轮动叶气膜冷却影响的三维非定常数值模拟［J］.热能动力工程，2011，26(5):507－512.

［13］杨子龙，肖蔚岩，王志强，等.涡轮叶片冷却通道换热特性研究［J］.热能动力工程，2013，28(4):241 －244.