心墙堆石坝坝坡稳定的有限元分析

贺立新

（湖南省发改委国家投资项目评审中心 长沙市 410007）

边坡稳定分析是堆石坝设计的前提，它决定坝坡是否失稳及可能存在的破坏形式，以便为土石坝结构设计提供科学依据。 目前工程应用最广的是需事先知道边坡滑动面位置和形状的极限平衡法。 在计算机和计算方法不断发展的背景下，尤其是岩土材料弹塑性有限元计算技术的发展，应用有限元法进行边坡稳定性分析多年来已经吸引许多工程研究人员的兴趣。

本文采用大型有限元分析软件ABAQUS，并结合强度折减法对某一堆石坝进行有限元分析，得到出塑性应变的发展及塑性区的范围及坝坡安全系数。 计算结果表明，采用此方法进行实际堆石坝的稳定性分析是合理地，且大大提高了计算效率。

1 有限元强度折减法

强度折减法就是在有限元计算中将边坡岩土体抗剪强度参数逐渐降低，直到土体破坏为止，其减少的倍数被定义为安全系数。强度折减法基本公式为：

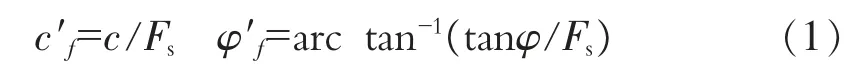
强度折减法的实质是在有限元计算中随着材料强度参数的降低，导致部分单元应力无法和强度配套，不能承受的应力转移到周围土体单元中，当出现连续滑动面之后，土体破坏。 其用剪切破坏面上实际土体强度与破坏时的强度比值来定义安全系数，和传统的极限平衡法是一致的。

2 ABAQUS在边坡稳定分析中的运用

ABAQUS 是世界上先进的大型通用有限元分析软件之一，得到了全球工程界和学术界广泛接受和认可。它在材料、几何与接触非线性等方面的分析能力居世界领先水平，可以准确地模拟土体这种特殊材料，在解决岩土力学中复杂的非线性问题方面优势显著，故在岩土工程分析中得到了广泛的应用。

2.1 本构模型的选取

正确地选择本构模型并合理地确定计算参数是数值计算成功的前提，有限元法中岩土体本构模型一般采用与传统极限平衡法刚塑性假设相对应的理想弹塑性模型，该模型可以分为Drucker-Prager（简称D-P 模型）和Mohr-Coulomb（简称M-C 模型）两大类。对于M-C 模型，因其公式简单，计算参数较容易获取，在岩土工程数值计算中得到广泛应用，本文选取该模型进行强度折减分析。 根据主应力以压应力为负的规定，可将MC 准则写成：

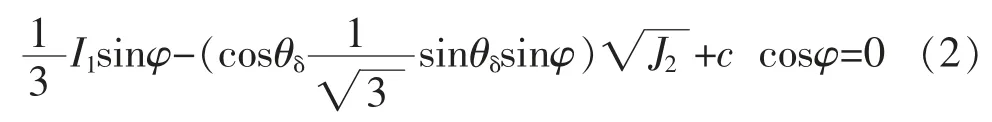
式中 I1、J2——分别是应力张量的第一不变量和应力偏张量的第二不变量；

θσ——应力罗德角；

c、φ——土体强度参数。

2.2 强度折减的实现

目前一些有限元软件中，如FLAC和Plaxis 等，都已内置强度折减法。 ABAQUS 虽然没有直接提供这种计算方法，但是实现起来也是相当方便的。首先将强度折减系数Fs定义为一个场变量，使材料参数随场变量而变化；再指定场变量的大小，并对模型施加重力和渗透力等荷载，平衡其应力状态，并线性增加场变量Fs，计算终止（数值不收敛）后对结果进行处理，按照失稳评价标准确定边坡的安全系数。 通过设置场变量，使得折减过程一步到位，而不需在一个指定的折减系数计算完之后，来判定需不需要进行下一步折减，大大简化了计算工作量。

3 工程应用

3.1 计算模型

以某一大型心墙堆石坝为例进行数值分析。 大坝典型断面、材料特性见表1。材料分区见图1、综合考虑数值解不收敛、特征点位移突变以及等效塑性应变贯通作为坝坡失稳的评判标准，对该堆石坝进行竣工期和稳定渗流期的坝坡稳定性分析，得到该堆石坝各工况下的坝坡稳定安全系数和滑裂面形状及位置。

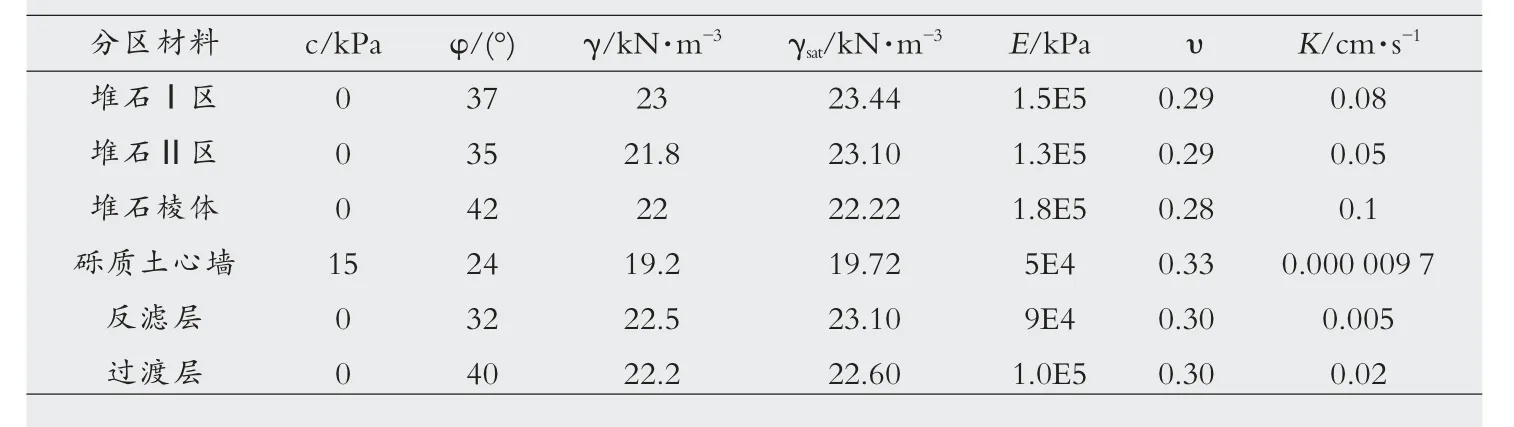
表1 坝体材料强度参数及渗透系数指标

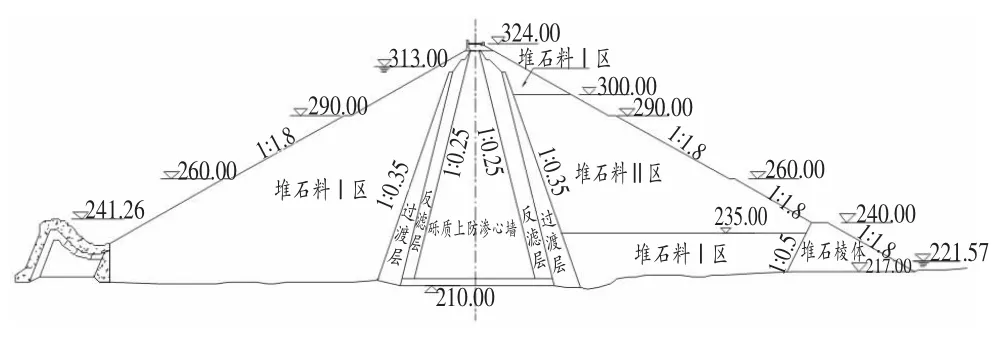
图1 某心墙堆石坝典型断面示意图（m）

3.2 计算结果

采用本文方法对坝体进行稳定分析，各工况下稳定安全系数见表2。

在不考虑渗流的竣工期，从图2～图3 中虽然可以看出特征点位移有明显的突变，但计算终止时位移不大（最大的位移0.027 m<<100 m），因坝高超过100 m，自然沉降等都会导致坝顶产生更大范围的位移，故单独采用位移突变作为边坡临界状态的标准，可能会导致分析结果的失真。 计算终止时的竣工期坝体位移矢量、等效塑性应变如图4～图5 所示，图中很难直观地看出塑性区有从坝顶到坡脚贯通的趋势，故采用等效塑性应变贯通作为边坡失稳的判别标准也有些牵强。 根据文献中所述内容，应综合考虑坝体特征点位移突变、坝体塑性区贯通、计算不收敛来进行边坡失稳的评判。 综合考虑以上因素，取安全系数Fs=1.347。 从图4～图5 中还可以看出坝体上下游都出现了塑性屈服区域，塑性屈服区域成圆弧状，有滑弧发展的动向，且滑弧很深，结果与堆石坝的一般稳定计算结果一致，符合一般计算规律。

表2 坝坡安全系数计算结果表

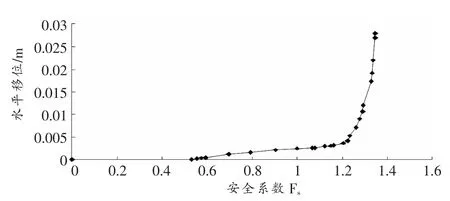
图2 蓄水期安全系数Fs与水平位移的关系

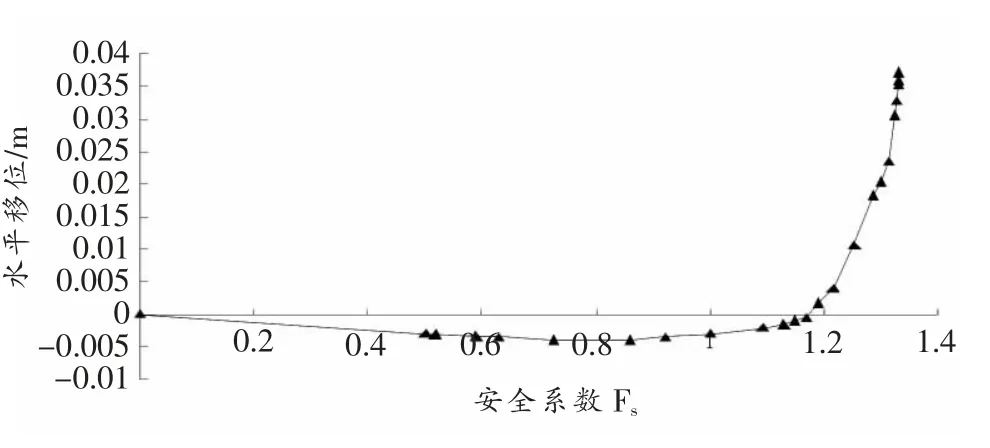
图3 稳定渗流期安全系数Fs与水平位移的关系

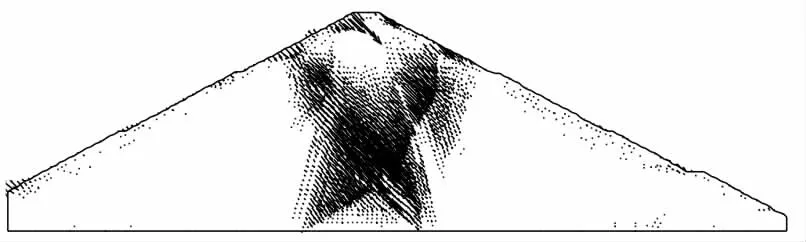
图4 蓄水期Fs=1.347 坝体水平位移矢量图

图5 竣工期Fs=1.347 时坝体等效塑性应变图

稳定渗流期时，图3 中特征点位移在Fs<1 的时候（此时强度参数还未折减，且强度参数比实际参数更大）因受到坝体自重、渗透力的作用，出现向上游发展的趋势；真实折减开始后（Fs>1），因土体强度参数的降低，特征点位移明显地倾向下游。 综合考虑坝体特征点位移突变、坝体塑性区贯通、计算不收敛对计算安全系数进行判别，取Fs=1.331，图6～图7给出了此时坝体的位移矢量、等效塑性应变图。 图中出现了两条塑性区分布，相比竣工期，此时的塑性区明显集中，深层滑动面更直观、更接近圆弧形状。此外，从图7 中可以清楚地看到上游土体的塑性应变是由坡顶开始向坡脚逐步发展，且在坝体中间出现了密集的位移矢量和塑性区分布，塑性区分布上游比下游更直观、清晰，同时还可以看出临界破坏时滑裂面的形状与一般极限平衡法的圆弧很吻合。可见，此法在分析坝坡稳定性上是直观的、简便的。

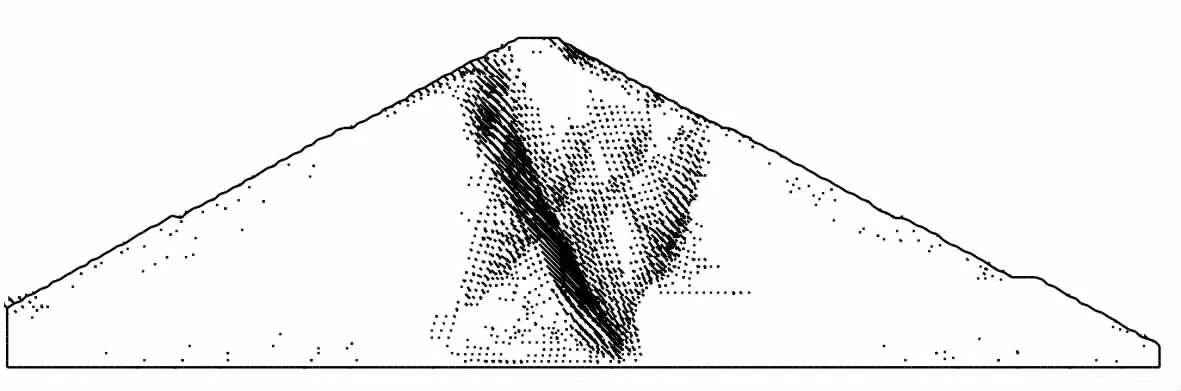
图6 稳定渗流期Fs=1.331 时坝体水平位移矢量图

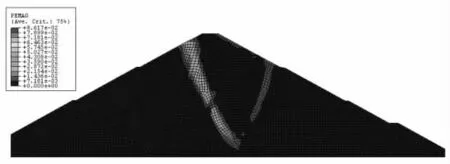
图7 稳定渗流期Fs=1.331 时坝体等效塑性应变图

4 结语

本文在使用强度折减法进行边坡稳定分析时，将折减系数Fs设为场变量，直接对强度参数进行线性折减。对某一心墙堆石坝进行坝坡稳定性分析，得到各工况下安全系数；同时利用ABAQUS 软件中强大的后处理功能，形象地描绘出边坡失稳形态，为准确判定边坡的真实受力状态提供可靠依据。 结果表明，由该法所确定的稳定安全系数和滑裂面分布符合一般规律，可以推广到考虑渗流作用的复杂土工边值问题的基坑工程，隧洞工程等。

1 Zienkiewieo C，Humpheson C，Lewis R.W.Associated and non-associated visco-plasticity and plasticity in soil mechanics[J].Geotechnique，1975，25（4）：671-689.

2 ABAQUS.Standard User's Manual [M].Hibbitte Karlsson&Sorenson INC，2002：26-78.

3 郑颖人，赵尚毅.岩土工程极限分析有限元法及其应用[J].土木工程学报，2005，38（1）：91－98.

4 张培文，陈祖煜；糯扎渡大坝设计边坡稳定的有限元分析[J].中国水利水电科学研究院学报；2003，03（12）：0207-0210.