中阶梯光栅铝膜的纳米压入测试

石广丰，徐志伟，史国权，蔡洪斌，王 磊，吕杨杨

（长春理工大学机电工程学院，长春130022）

0 引 言

在衍射光栅机械刻划工艺中影响光栅槽形的因素有很多［1］，其中光栅铝膜的力学性能是主要因素之一。光栅毛坯是三层复合式薄膜结构，在玻璃基底上首先镀制铬膜作为过渡连接层，再在上面真空镀铝。用金刚石刻划刀具刻划时，镀铝膜的弹塑性会对光栅槽形产生重要影响［2］。

长期以来，国内的光栅机械刻划制造是在未掌握光栅各膜层力学性能的情况下，通过金刚石刻划刀试刻多次，不断调整刻划工艺参数来实现的［1］。这种方法既不科学也不经济，显然不能满足现代高效、高精度光栅（如原刻母版光栅）的制作要求，因此采用模拟技术来研究机械刻划工艺的方法应运而生，而准确获得光栅铝膜的力学性能参数是采用模拟技术研究机械刻划工艺的前提［2］。目前，关于复合膜结构的力学性能研究报道很多，但是镀铝膜力学性能方面的研究成果很难应用于光栅铝膜上，而关于光栅铝膜力学性能的研究还鲜有报道。仪器化纳米压入技术结合有限元模拟技术反演求解复合薄膜弹塑性力学的方法已被广泛采用［3－4］。为此，作者尝试采用仪器化纳米压入测试技术和有限元模拟技术对槽线密度为79线·mm－1的中阶梯光栅铝膜的弹塑性应力－应变本构关系进行表征，并揭示相关影响规律。

1 试样制备与试验方法

试验用79线·mm－1中阶梯光栅毛坯结构由中科院长春光机所光栅室提供，采用真空蒸镀法制备。试样为铝膜／铬膜／玻璃基底的三层复合结构，如图1所示。其中，镀铝膜与镀铬膜的厚度分别为10，1μm，镀铬膜的弹性模量和泊松比分别为240GPa，0.3，玻璃基底的弹性模量和泊松比分别为70GPa，0.3。

图1 光栅毛坯横断面的SEM形貌Fig.1 SEM morphology of cross section of the grating blank

采用瑞士CSM公司的Nanohandness Tester型纳米压痕仪对中阶梯光栅毛坯的铝膜进行纳米压入试验，压头为金刚石Berkovich压头。压入深度需覆盖中阶梯光栅机械刻划的深度，选为3μm。通过控制位移的方式进行加载，时间10s，保载时间10s，卸载时间10s。

2 有限元分析

2.1 压入测试的有限元模型

采用ABAQUS模拟软件建立光栅镀铝膜层纳米压入测试的二维轴对称有限元模型，建模时用半锥角为70.3°的圆锥压头替代压痕试验中的玻氏压头［3］，光栅膜层的纳米压痕模拟模型如图2所示。

在不影响模拟精度的条件下，综合考虑求解速度，玻璃基底的厚度可以根据圣维南定理适当减薄［3］，同时对压入区域的网格进行加密处理，网格的总数为1 512。边界条件：左侧对称约束，右侧自由，底边固定，如图2所示。材料应力－应变关系遵循幂强化模型，假设材料为均匀且各向同性，屈服准则采用Von Mises屈服准则。另外，由于实际压入过程中加载速度比较慢，可以看作是准静态过程。压入模拟环境温度为20℃。

采用有限元模拟可以方便研究不同力学参数条件下铝膜纳米压入测试的载荷－位移响应情况，通过正交模拟分析，发现相关作用规律和初步优化组合，再通过迭代优化求解最优力学参数组合。最后可将最优力学参数组合重新输入压入过程的有限元模型，通过所得响应曲线与试验响应曲线的对比来验证优化结果的准确性。

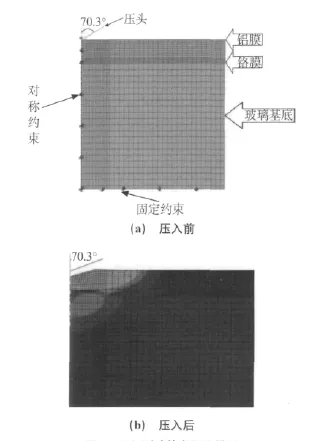
图2 压入测试的有限元模型Fig.2 FEM model of indentation：（a）before indentation and（b）after indentation

2.2 正交模拟

以某一压深时所得的模拟最大载荷Psmax与真实压痕试验的最大载荷平均值Pmean间的偏差Δ＝｜Psmax－Pmean｜最小化为优化目标，进行两因素四水平的完全压入正交模拟。两因素为待求光栅铝膜的塑性参数屈服应力σy和应变硬化指数n，四水平指σy（σy1＝100MPa，σy2＝200MPa，σy3＝300MPa，σy4＝400MPa），n（n1＝0，n2＝0.1，n2＝0.2，n3＝0.3），水平编号分别为1，2，3，4。由于铝属于塑性材料，这里n取至0.3即可。

3 结果与讨论

3.1 压痕试验结果

从图3中可以看出，数据曲线非常光滑，表明压入过程比较稳定可靠；在加载阶段载荷随着位移的增加而不断增加，在保载阶段位移不变载荷下降，随后卸载，材料产生一定的弹性回复，由此可知此压入过程主要是材料的塑性变形过程。根据Oliver－Pharr提出的经典力学方法［4］，求解铝膜弹性模量的平均值为85.7GPa，最大载荷平均值为215.95mN。

3.2 模拟结果

由图4可知，n与σy的增加会导致模拟压入过程中最大载荷变大。

图4 不同应变硬化指数下模拟的铝膜载荷－位移响应曲线Fig.4 Load－displacement response curves in different strain hardening exponents of aluminum film

从表1中可以看出，Rσy＞Rn，说明屈服应力σy对指标Δ的影响大于应力硬化指数n对指标的影响，优化目标Δ表示有限元压入模拟结果与真实压入试验的符合度，可见有限元模型的计算准确性对屈服应力值的输入最为敏感。

表1 正交分析表Tab.1 Table of orthogonal analysis

从表1中还可知，第6号试验结果Δ＝22mN，是所有数据的最小值，表明模拟数据与试验数据相差最小，可认为其对应的n＝0.1，σy＝200MPa为最优值。将所得屈服应力200MPa和应变硬化指数0.1代入压入测试的有限元模型，获得模拟的载荷与位移关系曲线（见图5）。从图5可知，压痕试验所得结果与模拟结果的偏差较大。根据以上分析所得屈服应力和应变硬化指数对指标Δ的影响规律，采用迭代正交优化的方法最终确定最优组合参数为屈服应力134MPa和应变硬化指数0.09。此时，模拟和试验所得的加载响应曲线之间的偏差很小（如图6）。最优组合参数所表征的该光栅铝膜应力－应变曲线如图7所示。需要说明的是，最终屈服应力和应变硬化指数取值可根据目标偏差值的大小继续优化，直到可以接受为止，视具体需求而定。

4 结 论

（1）获得了槽线密度79线·mm－1光栅铝膜的弹性模量为85.7GPa，根据有限元结合正交分析及迭代优化获得的测试最优屈服应力为134MPa、应变硬化指数为0.09。

（2）与应变硬化指数相比，所建立光栅压入测试有限元模型的计算准确性对屈服应力的输入较为敏感。

［1］巴音贺希格，高键翔，齐向东，等.9.77μm激光器零级耦合输出选频振荡光栅的设计和研制［J］.中国激光，2005，32（3）：301－305.

［2］SHI G F，SHI G Q，SONG L S.Modeling，simulation and a－nalysis of mechanical ruling echelle grating［J］.Advanced Material Research.2012，424：281－284.

［3］王洪祥，马恩财，高石，等.磷酸二氢钾（KDP）晶体纳米压痕过程的有限元分析［J］.材料科学与工艺，2009，17（1）：40－46.

［4］宋仲康，马德军，陈伟.材料力学性能纳米压入测试仪器发展综述［J］.装甲兵工程学院学报，2010，24（4）：45－49.