基于PSCAD/EMTDC的金卤灯仿真建模*
曾江 古智鹏 陈昌明 张祥华
(华南理工大学电力学院,广东广州510640)
金属卤化物灯(简称金卤灯)是把稀有金属的卤化物和蒸汽混合,并在混合物中产生电弧从而放电发光的高压气体放电灯.做为第三代光源,金卤灯具有发光效率高、显色性能好、寿命长等特点[1-8],目前广泛应用于体育场馆、展览中心、大型商场、工业厂房等场所的室内照明[1,6,9].
金卤灯启动过程中会呈现非线性特性,导致谐波畸变,而且存在负阻抗特性,所以需要采用控制装置(即镇流器)对灯进行控制[10].最初采用的电感式镇流器因工频噪声等缺点已逐渐退出使用,取代它的是运用电力电子技术的电子镇流器.电子镇流器具有节能、功率因数高、无闪烁和频闪效应、对供电电压有很好的适应性并可以提高灯管的寿命等优点.但它的运行过程会产生谐波,降低电能质量,最主要的缺点是会使金卤灯产生声谐振[11-12].
文中利用PSCAD/EMTDC仿真软件搭建金卤灯和电子镇流器的模型,模拟金卤灯的启动和稳定运行,得到金卤灯的电网侧电流并进行谐波分析,最后与深圳大运会场馆实测的金卤灯波形及频谱进行比较,证明文中搭建的金卤灯模型的准确性.
1 金卤灯的电气模型
1.1 建模方法
金卤灯是一个复杂的电气系统,它的放电过程包含了物理特性和化学特性的变化.近年来很多学者的研究方向是统一金卤灯的电气模型和物理模型,以建立一个可以利用通用软件仿真的模型,并且能较容易地确定模型中的参数.目前,关于金卤灯的建模主要分为3大类[6]:
(1)经验模型 通过测量金卤灯工作过程中的电压、电流、频率等参量随时间的变化,建立灯电阻与这些参数之间的函数关系[13].这种方法忽略了某些不必要的量,比较容易实现,但是模型需要多次试验仿真以选取最合适的一组数据,所以计算量较大,模型建立费时费力[14].
(2)物理模型 将微观粒子的运动状态和宏观的电压、电流、温度、电阻和频率等参数关联起来,根据气体放电理论、能量守恒原理和等离子体理论的方程,建立金卤灯模型[15-16],如文献[17]中通过汞离子和镝离子的演化过程和能量守恒等物理过程建立灯模型.这种模型与实际的变化还是存在一定差异.由于商业原因,每种灯的参数不同且难以得到,所以物理模型实现困难.
(3)曲线拟合模型 运用数学的方法对实验波形进行拟合,得到金卤灯参数曲线的表达式,从而得到金卤灯的数学模型,如文献[18]采用指数模型拟合灯电阻的变化曲线.曲线拟合方法既能满足建模精度的要求,又能用数学工具完成建模并加以仿真[3].
综合考虑上述3类金卤灯建模方法,由于曲线拟合方法较为简单,精度基本满足仿真要求,所以文中将采用曲线拟合方法来建立金卤灯的模型.
1.2 电气模型
由于金卤灯启动时有一个复杂的高电压情况,难以掌握这时的变化规律,而且这一过程的时间非常短[7],所以文中采用分时线性回归模型和多项式曲线拟合来求解启动高压之后的金卤灯启动波形曲线.分时线性回归方法的主要思想是在金卤灯启动到稳定过程的几段时间内,电压和电流随时间的变化规律近似地用一条直线来代替,所以在整个启动过程中,电压和电流的变化曲线可以看成是由几段线段构成的一条曲线.多项式曲线拟合则利用最小二乘法来求解曲线函数.图1为文献[2]中提到的2500W金卤灯的启动特性.
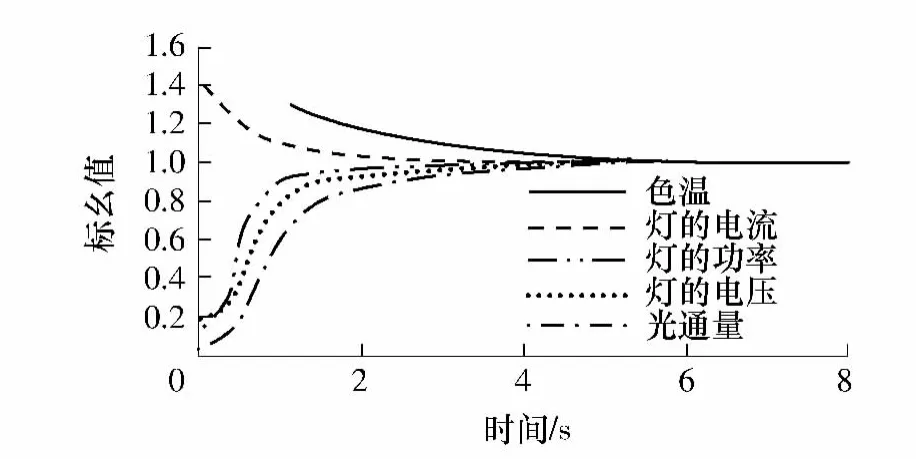
图1 金卤灯启动特性(2500W)Fig.1 Start characteristics of metal halide lamp(2500W)
1.2.1 分时线性回归拟合曲线
对于2500W的金卤灯,稳定工作时电压U0约为115V,电流I0约为21.7 A,用四段式曲线来模拟金卤灯在启动过程中的电压电流变化.
第Ⅰ段 从启动到开始的0.3 min内,t∈[0,t0],u0∈[0.20U0,0,30U0],i0∈[1.40I0,1.20I0]时,取t0=0.3min,瞬态电压、电流的表达式如下:

瞬态等效电阻:

第Ⅱ段 从0.3 min 到 1 min,t∈[t0,t1],u0∈[0.30U0,0.80U0],i0∈[1.20I0,1.05I0]时,取t1=1min,瞬态电压和电流的表达式如下:

瞬时等效电阻:

第Ⅲ段 从1 min 到 2.5 min,t∈[t1,t2],u0∈[0.80U0,U0],i0∈[1.05I0,I0]时,取t2=2.5min,瞬态电压和电流的表达式如下:

瞬态等效电阻:

第Ⅳ段 t∈[t2,∞]时,灯已经进入了稳定状态,电压和电流的线性表达式如下:

图2(a)、2(b)为金卤灯在启动过程中灯电压、电流、电阻的变化规律.
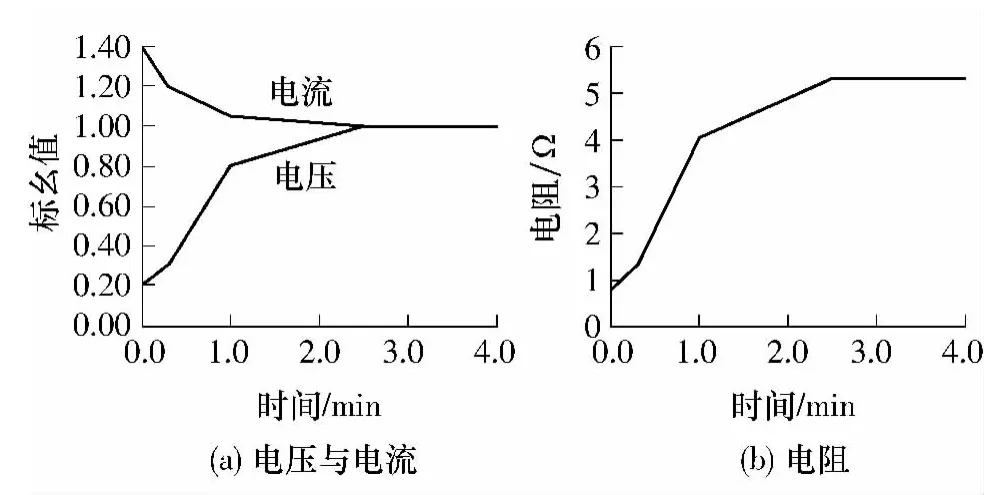
图2 分段线性拟合的金卤灯启动特性Fig.2 Start characteristic of metal halide lamp obtained by piecewise-linear fitting
1.2.2 多项式拟合曲线
文中用一类与数据的背景材料规律相适应的多项式表达式来反映电压、电流与时间之间的依赖关系,即在一定意义下最佳地逼近或拟合已知数据.多项式曲线拟合采用如表1所示采样点作为已知数据.

表1 金卤灯启动电压、电流曲线采样点Table 1 Sampling point of metal halide lamp starting voltage and current curve
拟合模型为f=a0+a1x+a2x2+…+anxn,由最小二乘法确定系数a0,a1,…,an,假设数据的加权为1,要求为最小,即要求各系数的导数为零,可得到方程:

式中,0为离散数据点起始点的下标,m为终点的下标,xi是离散数据点的横坐标,yi为离散数据点的纵坐标,r=0,1,…,n,n<m.
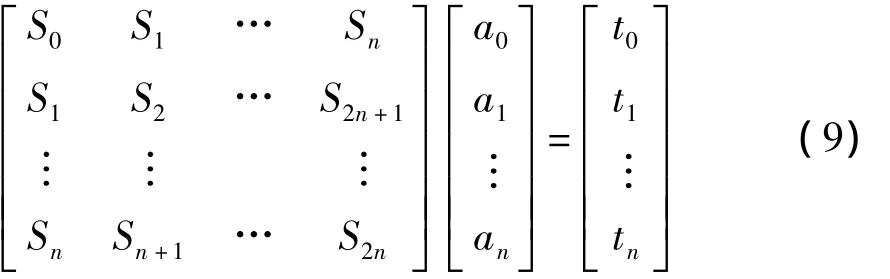
求解以上方程,可以得到多项式系数,则金卤灯电压、电流启动特性表达式如下:

多项式曲线拟合的金卤灯启动特性如图3所示,金卤灯启动时的伏安特性如图4所示.

图3 多项式曲线拟合的金卤灯启动特性Fig.3 Start characteristic of metal halide lamp obtained by polynomial curve fitting

图4 金卤灯启动时的伏安特性Fig.4 Startup voltage-current characteristics of metal halide lamp
由以上分析计算可知,分段线性回归模型和多项式曲线拟合模型都能满足精度要求,相比之下,多项式曲线拟合更精确,所以文中建议采用多项式曲线拟合模型进行仿真.
2 电子镇流器的电气模型
2.1 电子镇流器的原理
由于金卤灯具有低频负阻、高频正阻特性,为了使它正常工作,必须采用镇流器.文中的电子镇流器模型采用的是传统三级拓扑,其3部分具有独立的功能.如图5所示,第一级为功率因数校正电路,文中选择拓扑Boost型的功率因数校正电路;第二级电路为DC/DC电路,其主要功能是控制灯的电流和功率,这一级电路选择的拓扑为Buck电路;第三级电路为低频逆变电路,其主要功能是为金卤灯提供一个交变的工作电流和电压,而采用低频方波逆变的电子镇流器利用反馈系统增大输出阻抗,从而解决了金卤灯在低频工作时具有负阻特性的问题,提高了稳定性[4].

图5 电子镇流器的三级拓扑Fig.5 Three-level topology of the electronic ballast
根据上述的结构框图,建立了如图6所示的电路.

图6 金卤灯和电子镇流器的仿真模型Fig.6 Simulation model of metal halide lamp and electronic ballast
对于金卤灯的控制而言,第一级电路只需进行SPWM调制,保持稳定的输出电压和高功率因数,不需要该级电路调节灯电压和电流;分析第二级DC/DC电路时,可以将功率因数校正电路等效为一个直流电压源,将逆变电路和金卤灯等效为一个可变电阻;第三级逆变电路只需要改变逆变桥臂通断,不需要进行 PWM 调制[5].
2.2 电子镇流器的控制方式
(1)PFC-Boost电路的控制
由于电网电压为ui=Usinωt.其中,U为电网电压幅值,ω为角频率.
设在一个开关周期T内开关导通占空比为D,那么在稳态的一个周期T内,电感L两端的电压uL对时间的积分为0,即

结合文献[5]和[7]中的参数选择推导公式,可得

即
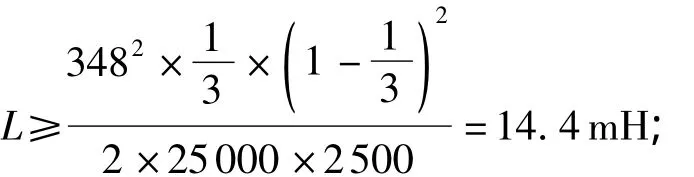
又有

即

式中,U0为该电路的输出电压,Ui为该电路的输入电压,P0为该电路的输出功率.
(2)Buck电路的控制
Buck电路主要是对金卤灯进行稳态控制,通过脉冲宽度调制,选取频率为25kHz,并在输出端并联一大电容,保持其输出功率基本不变,从而使金卤灯正常工作.
同样结合文献[5]和[7]中的参数选择推导公式,可得

即
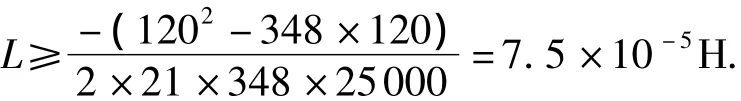
又有

即

式中,Δu为输出电压文波.
(3)全桥逆变电路的调制
为了防止电极极化,金卤灯除特殊场合使用直流工作外,几乎全部采用交流工作方式.电子镇流器在驱动金卤灯的时候,一般采用低频方波驱动,以防止“声谐振”,同时解决金卤灯在低频工作时具有负阻特性的问题,提高了稳定性.文中选取 f=150Hz、50%占空比的方波.
3 仿真结果与谐波分析
仿真电路中,电网侧线电压为380 V,同时连接3个金卤灯模型和电子镇流器模型,得到的电压、电流仿真结果如图7-11所示.

图7 单个金卤灯启动过程的灯电压、电流仿真波形Fig.7 Simulated voltage and current waveforms of metal halide lamp in its start process

图8 单个金卤灯稳定运行时电网侧的电流仿真波形Fig.8 Simulated stable grid-side current waveform of metal halide lamp

图9 多个金卤灯稳定运行时电网侧的电流仿真频谱Fig.9 Simuated stable grid-side current spectrum of multiple metal halide lamps

图10 深圳大运会场馆照明三相实测电流Fig.10 Measured current of Shenzhen Universiade Stadium lighting

图11 深圳大运会场馆照明A相实测电流频谱Fig.11 Measured A-phase current spectrum of Shenzhen Universiade Stadium lighting
通过单个金卤灯启动电压电流波形和多个金卤灯同时稳定运行时谐波频谱图的对比可以发现,所建模型电网侧电流波形与实测电流波形相差不大,模型的各次谐波电流变化规律与实测电流各次谐波的变化规律大致相同,都是以三次谐波为主,在现场测试中判断是配电线路中的电容器对11次谐波有放大作用导致实测11次谐波电流与仿真偏差较大.仿真模型的谐波电流总畸变率为

而实测数据的谐波电流总畸变率为
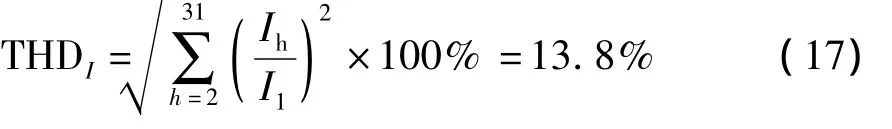
式中,I1为基波电流,Ih为谐波电流.
通过单个金卤灯启动电压电流波形和多个金卤灯同时稳定运行时谐波含量的分析、比较,可知仿真模型得到的结果和实测数据基本吻合,证明了此仿真模型具有一定的可行性和准确性.
4 结论
文中分别采用分段线性曲线拟合和多项式曲线拟合,利用PSCAD/EMTDC仿真软件建立金卤灯的启动模型,曲线拟合的结果与实测的金卤灯启动特性基本吻合.同时建立了三级电子镇流器模型,结合金卤灯模型在380 V电压等级下进行仿真,得到的结果在时域和频域上与深圳大运会场馆实测的金卤灯数据基本吻合,证明了模型是可行且准确的.
[1]李俊杰,刘汉奎,王议锋,等.一种大功率金卤灯电子镇流器的分析与设计[J].中国照明电器,2007,8:7-11.Li Jun-jie,Liu Han-kui,Wang Yi-feng,et al.Analysis and design of a high power metal halide electronic ballasts[J].China Light& Lighting,2007,8:7-11.
[2]金亦青.数字控制金卤灯用电子镇流器研究[D].浙江:浙江大学电气工程学院,2004.
[3]杨华.高强度气体放电灯镇流技术的研究[D].哈尔滨:哈尔滨工业大学电气工程及自动化学院,2009.
[4]朱国忠.高强度气体放电灯电子镇流器的研制[D].浙江:浙江大学电气工程学院,2007.
[5]吴小康.高功率金卤灯电子镇流器的研究[D].浙江:浙江大学电气工程学院,2010.
[6]朱国栋.HID灯整流效应的研究[D].哈尔滨:哈尔滨工业大学电气工程及自动化学院,2008.
[7]潘耀章.高强度气体放电灯及其电子镇流器系统的建模与仿真[D].哈尔滨:哈尔滨工业大学电气工程及自动化学院,2006.
[8]李妹,俞安琪.高强度气体放电灯镇流器的优缺点分析及改良应用[J].中国照明电器,2009,11:14-17.Li Mei,Yu An-qi.Analysis of the HID ballast’s advantages and disadvantages and its improved application [J].China Light& Lighting,2009,11:14-17.
[9]何新松,林国庆.高强度气体放电灯镇流器关键技术研究 [J].电工电气,2010,7:1-3.He Xin-song,Lin Guo-qing.Reasearch on key technology for high-intensity-discharge lamp ballast[J].Electrotechnics Electric,2010,7:1-3.
[10]Deng E,Cùk S.Negative incremental impedance and stability of fluorescent lamps[C]∥IEEE Applied Power Electronics Conference and Exposition.Atlanta:IEEE,1997:1050-1056.
[11]Dalla Costa,Marco A,Kirsten,et al.Analysis,design,and experimentation of a closed-loop metal halide lamp electronic ballast[J].IEEE Trans Ind Appl,2012,48(1):28-36.
[12]Yan W,Hui S Y R,Ho Y K E.Stability study and control methods for small-wattage high-intensity-discharge(HID)lamps[J].IEEE Trans Ind Appl,2001,37(5):1522-1530.
[13]Wei Yan,Hui S Y R.A universal PSpice model for HID lamps[J].IEEE Trans Ind Appl,2005,41(6):1594-1602.
[14]魏新劳,李家辉,王永红,等.高强度气体放电灯电气特性数学模型[J].电工技术学报,2010,25(6):123-129.Wei Xin-lao,Li Jia-hui,Wang Yong-hong,et al.Mathematical model for electrical characteristics of high intensity gaseous discharge lamp [J].Transactions of China Electro Technical Society,2010,25(6):123-129.
[15]Paul K C,Takemura T,Hiramoto T,et al.Development of a robust 3-D model for HID lamps and comparison of predicted and measured electrode temperatures[J].IEEE Trans on Plasma Science,2007,35(2):188-196.
[16]Paul K C,Takemura T,Hiramoto T,et al.Self-consistent model of HID lamp for design applications[J].IEEE Trans on Plasma Science,2006,34(4):1536-1547.
[17]Nimalasuriya T,Beks M L,Flikweert A J,et al.Metalhalide lamps in micro-gravity:experiment and model[J].Journal of Physics D:Applied Physics,2008,41(14):1-9.
[18]Juárez M A,Ponce M,Arau J,et al.Analysis and design of model based on step response for the stability in lamps HID[C]∥International Power Electronics Congress-CIEP.Cuernavaca:Institute of Electrical and Electronics Engineers Inc,2008:33-38.

