耦合场中轴向压缩碳纳米管的尺度效应*
姚小虎 陈达 欧智成 孙玉刚
(华南理工大学土木与交通学院,广东广州510640)
纳米技术是当今科研领域的热门技术课题之一,而碳纳米管的发现是其最有意义的突破之一.碳纳米管具有优异而独特的机械、力学、电学、化学和光学性能.完美的结构、小尺度、低密度、高硬度和高强度等性质使碳纳米管在材料增强、场发射平板显示器、传感器和纳米电子等领域获得了广阔的应用.
对于碳纳米管性能的研究,目前主要有纳米实验方法、原子级模拟方法和连续介质力学方法.由于受到纳米尺度的限制,碳纳米管力学行为的实验研究是非常困难的.当原子系统比较大时,原子级模拟所要的计算成本是比较高的,这就在实际应用中受到了很大的限制.因此,基于连续介质的力学方法近年来成为研究碳纳米管力学性能的主要方法之一.
尽管连续体模型在分析较大尺寸的碳纳米管力学问题时起了很重要的作用,但是连续体模型在求解的过程中并不允许涉及其内在尺寸的依赖性.因此不能使用经典连续体模型来研究碳纳米管的尺度效应问题.
非局部弹性理论主要用来解释弹性体中的尺度效应[1].Li等[2]运用非局部弹性理论对多壁碳纳米管的热屈曲进行了研究.Murmu等[3]基于非局部梁模型研究了单壁碳纳米管在温度变化和周围弹性介质影响下的屈曲问题,分别考虑了尺度和温度的影响.
作为纳米复合材料和纳米元器件基本单元的碳纳米管,其工作环境往往是复杂多变的.许多学者只对单个物理场作用下碳纳米管的屈曲行为进行了深入的研究,在热-电-力多场耦合作用下碳纳米管的屈曲行为则极少有人问津.Zhang等[4]用分子动力学方法研究了温度场对单壁碳纳米管受轴压、扭转和径向外压以及扭压组合荷载作用条件下的屈曲行为和后屈曲行为的影响,同时考虑了初始轴压作用下单壁碳纳米管的热屈曲问题.辛浩等[5]采用分子动力学方法分别对含缺陷扶手型碳纳米管和对应完善结构的碳纳米管进行轴向压缩模拟,通过比较两者在不同温度下的承载性能,发现完善结构的碳纳米管承载性能比含缺陷的碳纳米管承载性能更依赖温度.Yao等[6]基于经典连续介质力学板壳理论,对多壁纳米管在扭矩作用下屈曲受温度变化的影响做了深入分析.Zhang等[7]基于热弹性力学理论建立了弹性复合圆柱壳模型,对具有较大长细比受轴压作用的多壁碳纳米管受温度变化影响进行了探讨.Amin等[8]对热-力-电耦合作用下弹性介质中多壁氮化硼纳米管的轴压屈曲进行了研究.Ghorbanpour等[9]考虑尺度效应,对双壁碳纳米管进行了热屈曲的研究.Ansari等[10]基于非局部弹性理论与多壁弹性壳模型,研究了温度变化下碳纳米管的轴压屈曲问题.Narendar等[11]基于非局部弹性梁理论对单壁碳纳米管进行了热屈曲的研究.结合非局部弹性理论的热屈曲问题的研究还有很多[12-14],但是基于非局部弹性理论研究多物理场耦合作用下的屈曲问题则极少有人涉及.
基于非局部弹性理论,文中采用弹性壳体模型,计及多壁碳纳米管层间范德华力的影响,建立了热-电-力多场耦合作用下考虑碳纳米管尺度效应的屈曲控制方程,从理论上推导与分析多壁碳纳米管在多场作用下的轴压屈曲条件,并给出双壁碳纳米管轴向屈曲临界载荷的解析解,对其进行参数研究,以期为碳纳管的应用与设计提供有价值的依据.
1 非局部理论的本构关系
在经典弹性理论模型中,弹性体内的一点x的应力只取决于该点的应变,而在Eringen的非局部弹性模型[15]中,弹性体内某一参考点x点的应力不仅取决于x点的应变,而且与体内所有其他点的应变相关.非局部理论[8]与经典弹性理论的区别就在于x点以外的点对x点的影响,经典弹性理论的本构关系是忽略了x点以外点的应变影响.对于非局部弹性理论来说,最一般的本构方程形式包含了一个对整个目标区域的积分.因为非局部弹性本构方程涉及到空间积分,该积分体现了体内所有点的应变张量对给定点应力张量贡献的加权平均,这导致了求解非局部弹性问题解析解的困难.然而,Eringen[15]指出对于一些核函数,积分本构方程可以完全转化成一个等价的微分形式.因此我们可以得到非局部理论的本构关系为
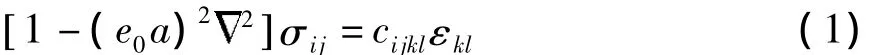
式中,σij为经典应力张量,cijkl为经典刚度张量,εkl为经典应变张量,2为拉普拉斯算子,e0为与每种材料相对应的常数,需要通过相关的实验或分子模拟获得,a为内部特征长度(例如C—C键的长度、晶格长度、颗粒距离等).
2 屈曲控制方程
下式是热-电-力多场耦合作用下的应力-应变关系[8]:
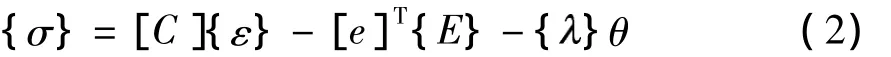
式中,{σ}、{ε}、{E}和{}分别表示应力、应变、电场和温度应力系数,θ表示温度变化值,[C]和[e]T分别表示弹性刚度矩阵和压电系数.每个系数的值取决于材料的结构性质.
Sai和Mele[16]的研究结果表明,锯齿型碳纳米管与扶手椅型碳纳米管在压电反应上有着不同的性质,锯齿型碳纳米管表现出纵向的单轴应变(拉伸或者压缩)的压电反应,而扶手椅型碳纳米管则表现出与扭矩耦合的电偶极子力矩,所以两者在热-电-力多场耦合作用下的应力应变具体形式是有所区别的,但在推导多壁碳纳米管屈曲控制方程时可以得到一个统一的形式,文中因为是做轴压载荷的研究,所以将以锯齿型碳纳米管为模型.
以弹性圆柱壳为模型,其壳体厚度为t,半径为r,u、v和w分别代表壳中面的轴向位移(x轴)、环向位移(y轴)和径向位移(z轴).结合非局部理论的本构方程(1),可以给出基于非局部弹性理论多场耦合作用下弹性壳的线性屈曲控制方程:
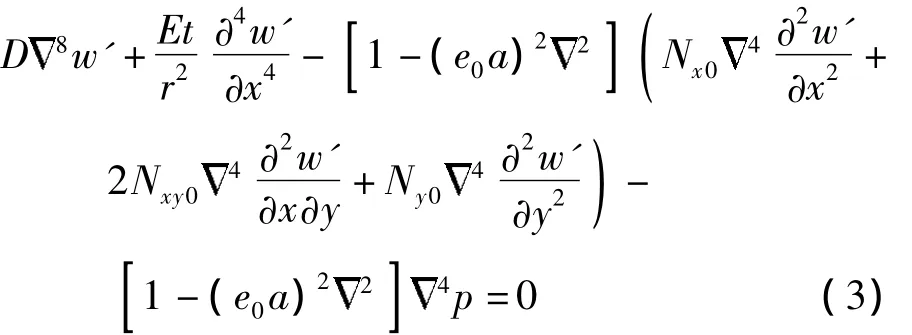
式中:D=Et3/[12(1- ν2)],为有效弯曲刚度,E 为壳的弹性模量,ν为壳的泊松比;Nx0、Ny0和 Nxy0为相应方向的前屈曲临界载荷,包含着热、电、力场引起的载荷;w'为屈曲径向位移增量,p为屈曲径向力增量.
由于碳纳米管层间存在范德华力的作用,最外层碳纳米管可能会受到弹性介质基体的作用,碳纳米管周围弹性介质基体对碳纳米管最外层的作用可以看作为弹性常数为k的“弹簧”作用,这些量都将体现在屈曲控制方程的屈曲径向力增量p上.假设研究的多壁碳纳米管层数为n,即有
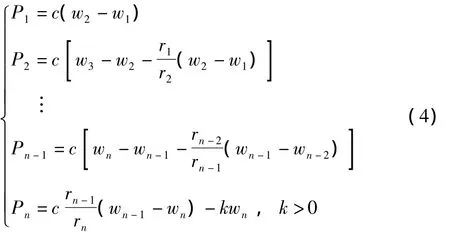
式中:Pi代表第i层管的法向力增量;wi表示第i层管径向位移增量,为简便且在不引起混淆情况下略去增量位移上标;ri表示为第i层管半径;c为范德华常数,采用以下取值[17]
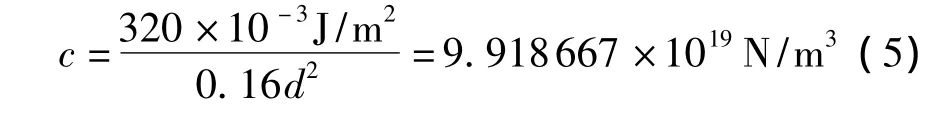
式中,d=1.42×10m.
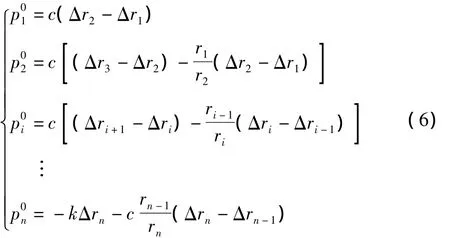
式中,Δri为第i层管半径变化量.根据应变的关系,容易得到:从而得出与NxiM的关系.

对于多壁碳纳米管而言,在屈曲前由于轴向压缩载荷引起的层间距的变化量为零.换言之,在临界屈曲发生前由机械载荷引起的范德华力为零.同样地,可以认为屈曲前由轴向压缩载荷引起的最外层和弹性介质之间的压力为零.但是温度的改变能够使所有管在法线方向膨胀或者收缩,则屈曲前由热载荷引起的每层管的范德华力和最外层管与弹性介质之间的压力不能忽略.
假定各层碳纳米管所受轴压荷载相等,设各层单位长度轴向载荷为Fx,温度均匀改变量为T,轴向电场强度为Ex,则有:
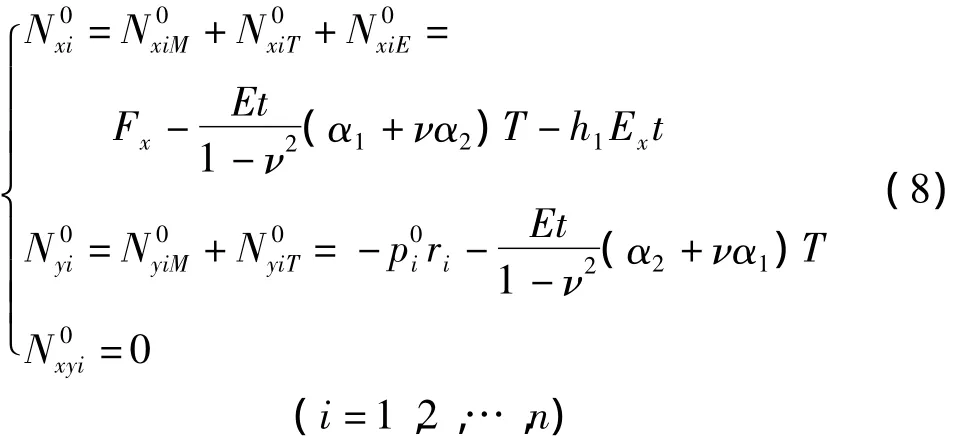
综上所述,可以建立基于非局部弹性理论的热-电-力耦合作用下n层碳纳米管的屈曲控制方程:
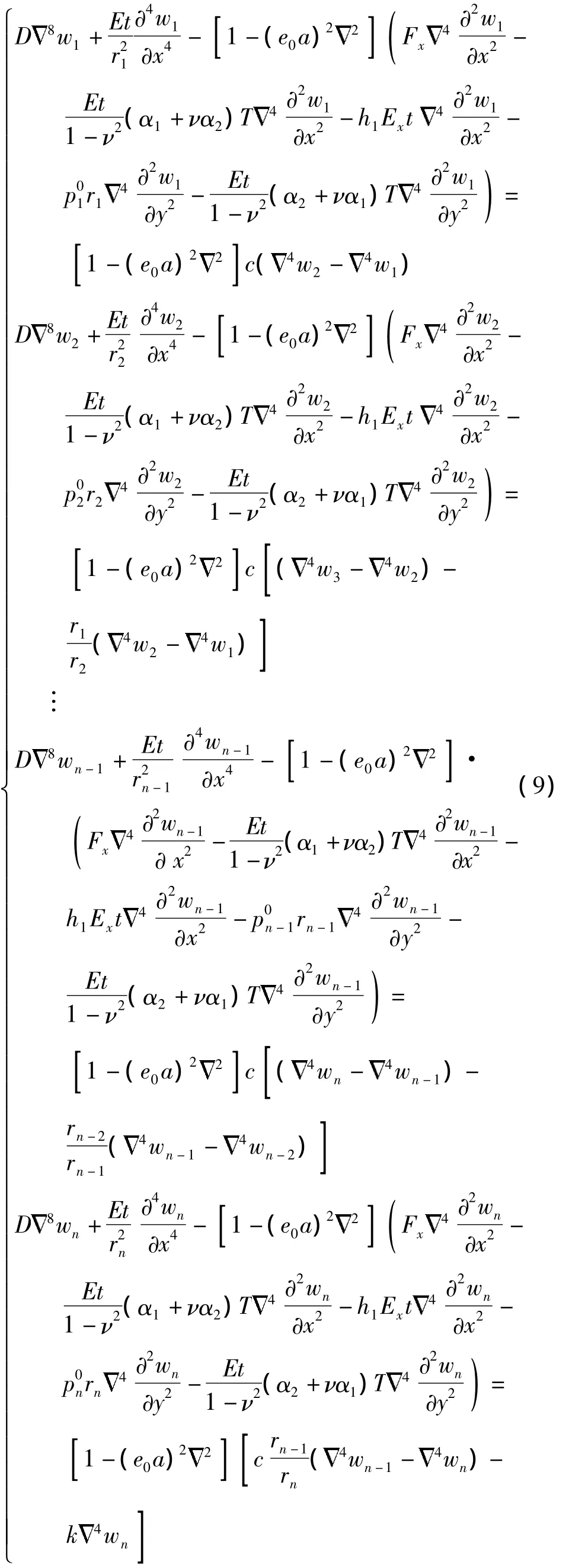
以双壁碳纳米管为例,从理论上可以给出双壁碳纳米管临界轴压屈曲载荷的解析表达式.
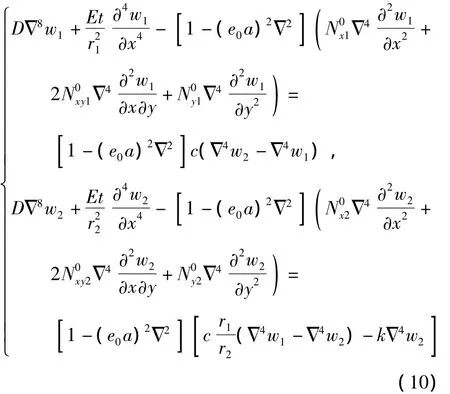
取n=2,则基于非局部理论多场耦合作用下双壁碳纳米管的屈曲控制方程为式中,N0x1、N0xy1、N0y1、N0x2、N0xy2、N0y2是由热、电和力场耦合作用产生的前屈曲载荷.
由于圆柱壳的临界屈曲载荷对其边界条件是不敏感的,在文中假定考虑简支边界条件,其位移模式如下:
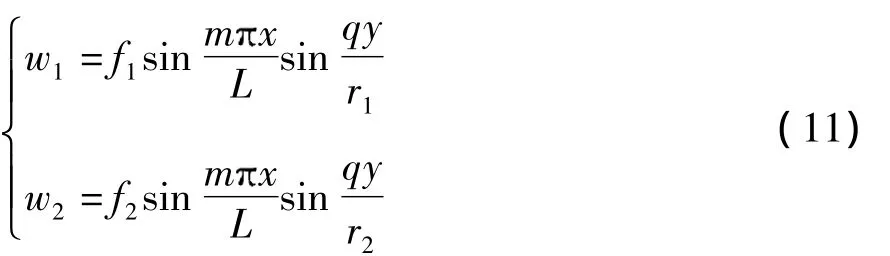
式中,r1、r2为双壁碳纳米管内、外管半径,L为碳纳米管的管长,f1、f2为实常数,m、q分别为碳纳米管的轴向波数和周向波数.
根据f1、f2取到非零解的条件,可以得出临界轴压屈曲载荷Fx的解析表达式.
3 结果分析

数值计算选取的共同参数具体如下:
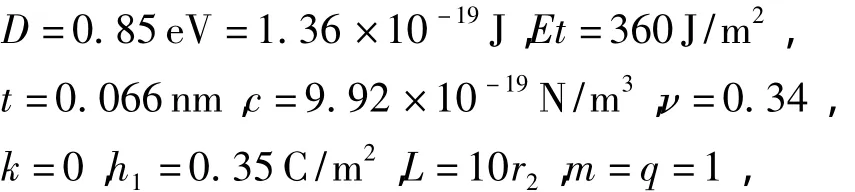
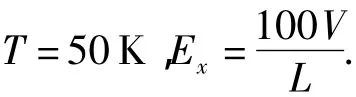
低温和室温时取:
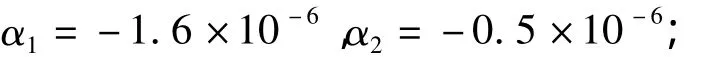
高温时取:

当图中所用数据与上述数据不同时将会在对应的图中给出.

图1 不同e0a时φ与r1的关系曲线Fig.1 Relation curves between φ and r1with different e0a
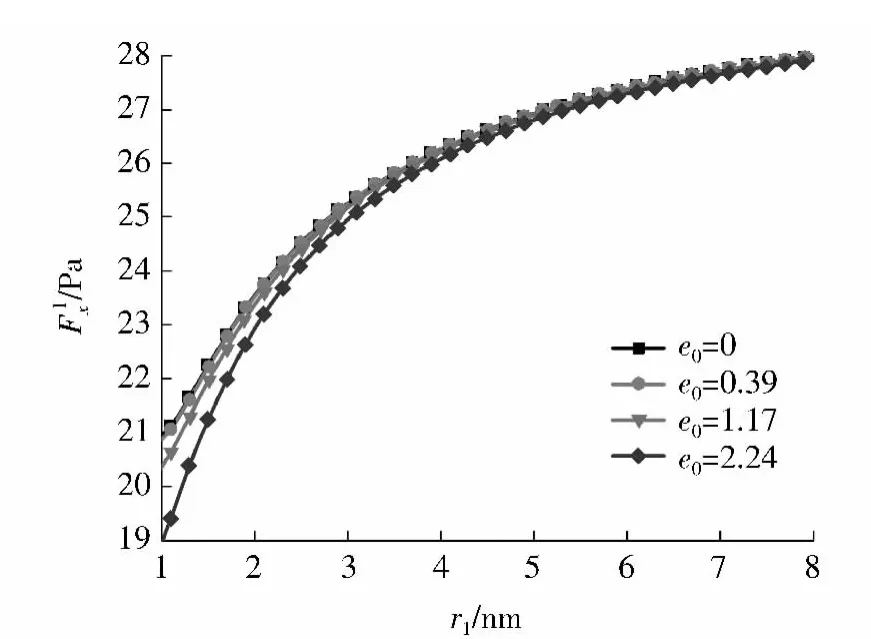
图2 不同e0时与r1的关系曲线Fig.2 Relation curves betweenand r1with different e0
图1与图2分别是无量纲参数φ和临界轴压屈曲载荷Fx与双壁碳纳米管内半径r1的关系曲线,其中r2=r1+0.34nm.从图1可以看出,当以e0a为一组合的参数时,取不同的e0a值,φ始终小于1,且φ会随着r1的增大而越来越接近1,说明经典理论下的临界轴压屈曲载荷是偏大的.从曲线的前部分来看,也就是r1很小的时候,φ比1小得多或比较小,说明此时采用非局部理论得到的临界轴压屈曲载荷比利用经典弹性理论得到的临界轴压屈曲载荷要小很多,表明小尺度效应显著.在该尺度范围内,经典理论下的临界轴压屈曲载荷是偏大很多的,经典理论已经不适合运用在该尺度范围.从曲线的后半部分来看,也就是r1比较大的时候,φ几乎接近1,说明此时非局部理论下的临界轴压屈曲载荷与经典理论下临界轴压屈曲载荷是相近的,表明尺度效应已经不再显著,在该尺度范围,经典理论分析不会产生太大的误差.图2中,仅考虑e0单独变化的影响,对比不同曲线,e0越大,小尺度效应越大,可以看到e0越大,其对应的临界轴压屈曲载荷F1x越小;当双壁碳纳米管内半径r1增大时,其小尺度效应相对会变小,所以会逐渐接近经典理论下的临界轴压屈曲载荷,因而各曲线会越来越接近,从而趋向一个相同的值.文献[10]中对多壁碳纳米管轴压屈曲问题进行数值分析,得到的结论是屈曲载荷比会随着非局部参数e0a的增大而减小,屈曲载荷比小于1,并且当e0a很大时,屈曲载荷比是远小于1的,这说明小尺度效应会使多壁碳纳米管更容易屈曲.这与图1和图2得到的结论一致.
图3与图4分别给出了在高温与低温环境下,临界轴压屈曲载荷F1x与温度变化量T的关系曲线,其中 r1=0.35nm,r2=0.70 nm.从图3 与图 4可以看出,在高温与低温环境下,以e0a为一组合参数,取不同的e0a,非局部理论下的临界轴压屈曲载荷与温度变化量T的关系是线性的,而且在高温环
境下是负线性的,在低温环境下是正线性的.这说明高温或低温环境下,温度上升会导致临界轴压屈曲载荷的减少或增加.该结果与前面的研究[18]是吻合的,碳纳米管热膨胀系数在低温或室温下是负值,而在高温下是正值.从不同的e0a的曲线来看,不同e0a代表不同程度的小尺度效应,而e0a的不同,并没有改变临界轴压屈曲载荷与相应温度环境下温度变化量的线性关系,只是小尺度效应越大,其对应的临界轴压屈曲载荷越小或越大.
图5是在低温环境下,临界轴压屈曲载荷F1x与电压U的关系曲线,其中r1=0.35nm,r2=0.70nm.从图5可知,以e0a为一组合参数,取不同的e0a,非局部理论下的临界轴压屈曲载荷F1x与电压U的关系是线性的,而且是负线性的.说明低温环境下,电压的上升会导致临界轴压屈曲载荷的下降.从不同的e0a的曲线来看,不同e0a代表不同程度的小尺度效应,而e0a的不同并没有改变临界轴压屈曲载荷与高温环境下温度变化量的负线性关系,只是小尺度效应越大的,其对应的临界轴压屈曲载荷就越小.
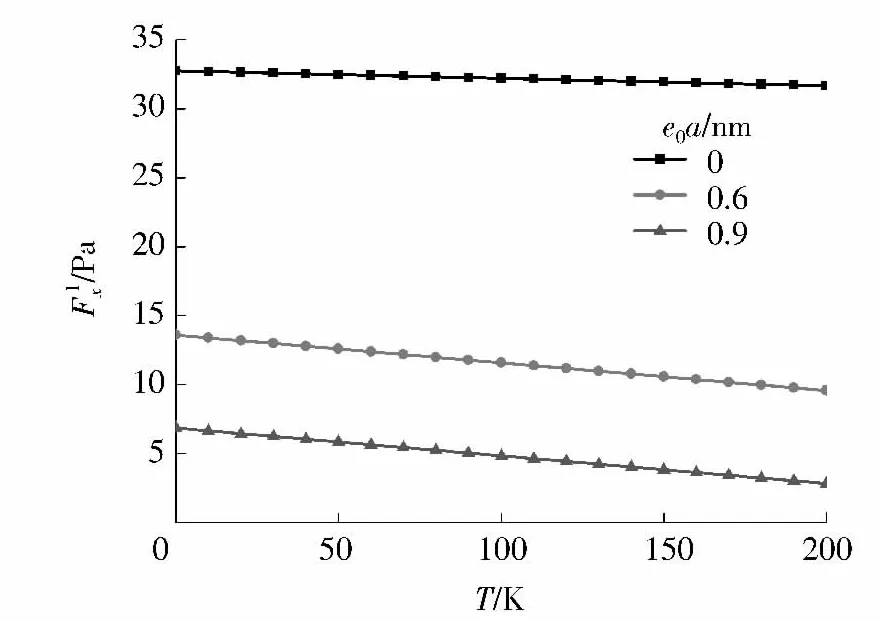
图3 不同e0a时F1x与T(高温)的关系曲线Fig.3 Relation curves betweenand T with different e0a(at high temperature)

图4 不同e0a时与T(低温)的关系曲线Fig.4 Relation curves between and T with different e0a(at low temperature)
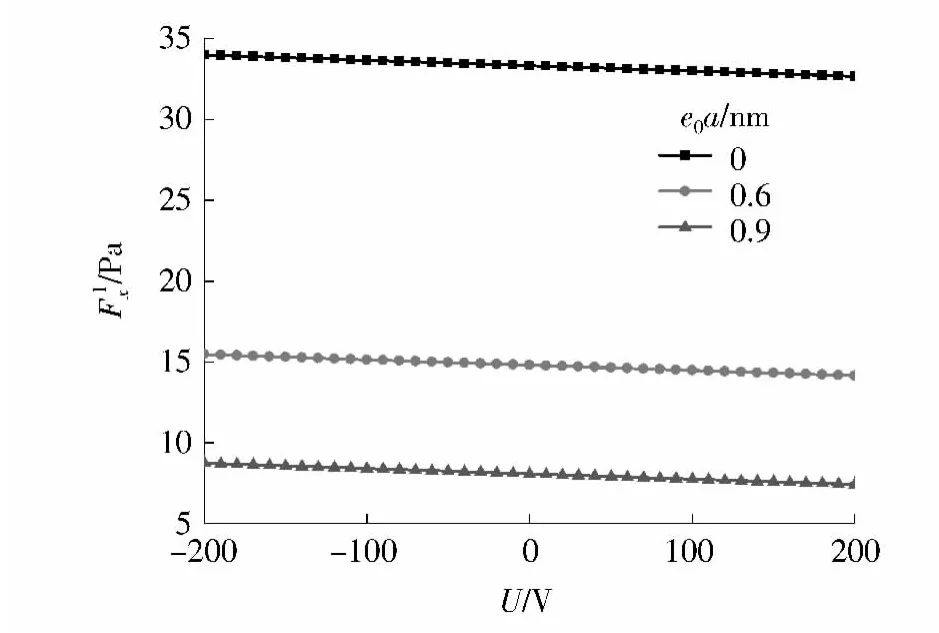
图5 不同e0a时与U的关系曲线Fig.5 Relation curves betweenand U with different e0a
4 结论
通过前面数值分析,可以得出以下结论:
(1)在小尺度范围内,经典理论对临界轴压屈曲载荷的分析是高估的,是不适用的,应当用非局部理论来分析;而在比较大的尺度范围内,经典理论对临界轴压屈曲载荷的分析是可以接受的.
(2)温度场的变化和临界轴压屈曲载荷的关系是线性的,高温情况下是负线性关系,低温情况下是正线性关系.
(3)电场的变化和临界轴压屈曲载荷的关系是负线性关系.
(4)通过单独变化e0和e0a,能够看出在较小半径时临界轴压屈曲载荷在不同小尺度效应下的值是不同的,说明小尺度效应在此时影响很大;而在较大半径时,临界轴压屈曲载荷在不同尺度效应下的值是很接近的,说明小尺度效应的影响可以忽略不计.
[1]Eringen A C,Edelen D G B.On nonlocal elasticity[J].International Journal of Engineering Science,1972,10(3):233-248.
[2]Li Renfu,Kardomateas George A.Thermal buckling of multi-walled carbon nanotubes by nonlocal elasticity[J].Journal of Applied Mechanics,2007,74(3):399-405.
[3]Murmu T,Pradhan S C.Thermal effects on the stability of embedded carbon nanotubes[J].Computational Materials Science,2010,47(3):721-726.
[4]Zhang L C,Shen H S.Buckling and post buckling of single-walled carbon nanotubes under combined axial compression and torsion in the thermal environments[J].Physical Review B,2007,75(4):045408.
[5]辛浩,韩强,姚小虎.缺陷对单层碳纳米管轴压屈曲性能的影响[J].华南理工大学学报:自然科学版,2008,36(6):52-55.Xin Hao,Han Qiang,Yao Xiao-hu.Influences of defects on buckling properties of single-wall carbon nanotubes under axial compression[J].Journal of South China University of Technology:Natural Science Edition,2008,36(6):52-55.
[6]Yao X H,Han Q.Buckling analysis of multiwalled carbon nanotubes under torsional load coupling with temperature change[J].Journal of Engineering Materials and Technology,2006,128(3):419-427.
[7]Zhang Y Q,Liu X,Zhao J H.Influence of temperature change on column buckling of multiwalled carbon nanotubes[J].Physics Letters A,2008,372(10):1676-1681.
[8]Amin Salehi-Khojin,Nader Jalili.Axially compressed buckling of an embedded boron nitride nanaoube subjected to thermo-electro-mechanical loadings[J].Behavior and Mechanics of Multifunctional and Composite Materials,2007,6526:652621.
[9]Ghorbanpour Arani A,Mohammadimehr M,Saidi A R,et al.Thermal buckling analysis of double-walled carbon nanotubes considering the small-length effect[J].Mechanical Engineering Science,2011,225(1):248-256.
[10]Ansari R,Rouhi H,Sahmani S.Thermal effect on axial buckling behavior of multi-walled carbon nanotubes based on nonlocal shell model[J].Physica E:Low-dimensional Systems and Nanostructures,2011,44(2):373-378.
[11]Narendar S,Gopalakrishnan S.Critical buckling temperature of single-walled carbon nantubes embedded in a one-paremeter elastic medium based on nonlocal continuum mechanics[J].Physica E Low-dimensional Systems and Nanostructures,2011,43(6):1185-1191.
[12]Khaled Amara,Abdelouahed Tounsi,Ismail Mechab,et al.Nonlocal elasticay effect on column buckling of multiwalled carbon nanotubes under temperature field[J].Applied Mathematical Modelling,2010,34(12):3933-3942.
[13]Yan Y,Wang W Q,Zhang L X.Nonlocal effect on axially compressed buckling of triple-walled carbon nanotubes under temperature field [J].Applied Mathematical Modelling,2010,34(11):3422-3429.
[14]Ansari R,Sahmani S,Rouhi H.Axial buckling analysis of single-walled carbon nanotubes in thermal environments via the Rayleigh-Ritz technique [J].Computational Materials Science,2011,50(10):3050-3055.
[15]Eringen A C.On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves[J].Journal of Applied Physics,1983,54(9):4703-4710.
[16]Sai N,Mele E J.Microscopic theory for nanotube piezoelectricity [J].Physical Review B,2003,68(24):241405.
[17]Saito R,Matsuo R,Kimura T,et al.Anomalous potential barrier of double-wall carbon nanotube[J].Chemical Physics Letters,2001,348(3/4):187-193.
[18]Jiang H,Liu B,Huang Y,et al.Thermal expansion of single wall carbon nanotubes[J].Journal of Engineering Materials and Technology,2004,126(3):265-270.

