基于遗传算法的分组算法

李 峰， 王海英

（东北石油大学 计算机科学系，黑龙江 大庆 163311）

1 分组策略

协作学习过程中，教师要依据学生个人特征和分组策略进行合理分组。学生通过测试可以得到一些个人特征，每次的学习活动也将被记录档案，这都是分组的重要依据。每小组一般以3～6人为宜，每组选一个组长。分组时，可以有意识的根据学习者特征进行优化组合，优差生共同进步。让学生充分发挥自身优势的同时，在某些弱势方面教师也要分配其适量的任务，并加以辅导协助，循序渐进，使其得到锻炼、增加自信心。经过教学分析和实践检验，得到分组时应从以下两方面考虑。

1.1 组内异质，组间同质[1]

组内异质指小组成员间在专业知识、年龄、性别、学习风格、学习动机等方面具有差异性，组间同质指各小组之间大体均衡，这样小组间才有可比性。组内异质可为小组成员之间的互助协作奠定基础，而组间同质又可为各小组间的公平竞争创造条件。

1.2 公平竞争、合理比较

组员间既存在协作也存在良性竞争，为了能让小组取得好成绩，组员们都会尽自己最大努力。组间的竞争使得学习者之间更具有凝聚力，能够充分发挥出团队的作用。在分组时，要注意公平合理，避免学生因感到人员分配不合理而丧失积极性。

2 基于遗传算法的分组算法

前面已经介绍了分组的重要性，也介绍了一些理论及注意事项。若是教师对所教授班级的学生不算了解，分组则会带来一定的风险。在研究了一些现有分组算法如杨友林[2]提出的“基于模糊C均值算法”、李杰[3]的“最优化理论算法”后，文中提出了“基于遗传算法的自动分组”的算法。与张春玲[4]的遗传算法分组不同，算法在编码的定义、适应度函数的计算、遗传操作等方面都有所改变。算法严格遵循“组间同质，组内异质”的分组原则，并在初始化序列、组长选择方面做了一些优化。遗传算法是一种通过模拟自然进化过程搜索最优解的方法，1975年，J.Holland教授首先提出并出版了颇有影响的专著《Adaptation in Natural and Artificial Systems》，GA这个名称才逐渐为人所知，J.Holland教授所提出的GA通常为简单遗传算法（SGA）[5]。遗传算法是一种基于自然选择和自然遗传的全局优化算法，用遗传算法对多个个体组成的群体进行操作，通过遗传算子可以使个体间的信息得以交换，这样的群体中的个体一代一代地得以优化，并逐步逼近最优解[6]。遗传算法分组效果的好坏关键是适应度函数的选取，而执行时间与初始序列有很大的关系，文中针对这两方面在算法上做了一些优化改进。

具体分组过程：

依据每个学生的特征，本着“组内异质，组间同质”的原则进行分组，本次分组主要考虑学生特征中的学习风格、学习动机、学科背景和协作能力。学习风格通过附录试卷测试测出学习者属于“活跃型与沉思型、感悟型与直觉型、视觉型与言语型、序列型与综合型[7]”中的哪4种类型（每组会得出一种类型）；学习动机通过附录试卷测出学习者属于“动机强”、“动机中”还是“动机弱”，并给出具体分值；学科背景则从学校教务系统中导出学生成绩，将本次协作涉及到的学科成绩取平均值作为学生的一个特征向量（百分制）；协作能力分值可以从上一次协作评价记录中提取，若初次使用这种协作学习方式则默认为60分。这样就可以用四元组对学习者进行描述：学习者（学习成绩，学习风格，学习动机，协作能力）规定符号表示为L（A，S，M，C）。学习成绩和协作能力我们已经量化，学习动机分数也可以从测试卷中得到（满分36分，计算时可转换为百分制），学习风格本身是用一个四维向量描述的，且各个向量没有相互关系。为方便遗传算法做差异计算，规定“活跃型、感悟型、视觉型、序列型”用“1”表示，“沉思型、直觉型、言语型、综合型”用“0”表示，例如一个学习者是“活跃型、感悟型、视觉型、序列型”，可以用“10101010”表示，两个学习者做“与运算”，可以通过累计“1”的数量来量化学习者间的风格差异。如果运算后没有“1”，表示无差异，认为两个学习者风格相同，若风格完全不同，则会出现4个“1”，差异值为100分。为了算法排序计算方便，将学习者风格“活跃型、感悟型、视觉型、序列型”设为标准，每个学习者与这个标准的风格差异值作为这个学习者的学习风格值，也就是学习者风格转化的二进制数与“10101010”做“与运算”之后，将所得数列位上“1”的个数乘以“10”后加上“60”的值作为学习者风格量化后的值，例如经过“与运算”有3个“1”，则差异值为90分。最后加分值是为了避免分组因风格差异分值大而使分组变成以“学习风格”划分为主。

2.1 初始种群

已知本遗传算法中的一个因子可以用一个四元组表示，假设班级学生人数为n，要分成m组，前面已经说明每组以3～6人为宜，当小组人数不能平均分配时，若剩余人数多于正常小组人数一半时，则单独划分一个小组，否则选择若干小组各多分配一人。第i（i＝1，2，…，n）个学生的基本情况作为一个因子用Li表示：Li＝（Ai，Si，Mi，Ci），不同于以往的遗传算法编码，由于要进行多个分组，文中提出用学生学号作为染色体上的一个基因，描述一次分组情况的序列作为一个染色体。良好的初始序列，将大大减少遗传算法中的迭代次数，缩短运行时间。下面就开始初始化序列，先将描述基因个体四元组中元素用百分制表示出来，计算出每个个体的一个初始分值：

式中：W1，W2，W3，W4—— 权值，一般默认每个权值为0.25，教师可以根据课程的侧重点不同进行更改设置。

将初始的m个值进行降序排列，需要强调的是，在分组前经过试卷调查和教师的确认，已经确定了各组组长，所以要将各组组长移到序列前端，并记录好组长的位置。初始矩阵的前m个值为各组组长，并在后期不参与各种遗传操作，但进行差异计算。对剩余的n－m个学习者进行初次分组，采取等间隔方法，就是将剩余学习者分为m组，L（1）至L（m）为各组组长，其他为组员。我们可以初始化给出k个个体，即染色体（执行分组前给出初始值），每个个体都是是由一组学号组成。其余k－1个个体的选择，依然不动组长位置，将剩余的n－m个个体（降序排列）分为m份，若不能平均分配时，按前面叙述原则，有一组人数较其他组少成员或一些组将剩余人员各取1人。此时随机从每份选择1人形成一个组，一次重新分组序列作为一个种群个体。在这k－1个个体中，除组长位置，也可以留些个体，不排序划分，随机提取人员与组长组成一组，这样会使得个体具有多样化，有利于取得最优值。

2.2 适应度函数计算

对于每个学生都已经获知了其初始分值，共n个值，在保证各组组长不换动的情况下，应尽量让“组间同质”，即让每组的平均分值大体相当；另外，经过遗传操作使得“组内异质”，即同学间的差异度尽量大，可以通过前文提到的四元组进行量化比较，首先可以得到各组内部的平均特征量化公式：

两个学习者间的差异公式：

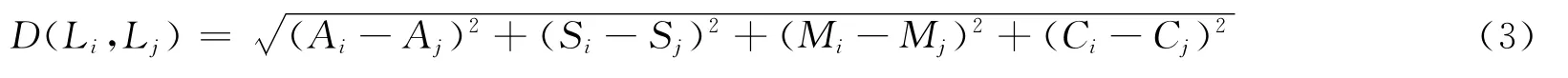
两个小组间的差异公式为：

在进行计算时，要分别计算一个分组序列整体的组内差异和组间差异，组内差异是小组内部学习者之间各自差异和再进行汇总，公式为：

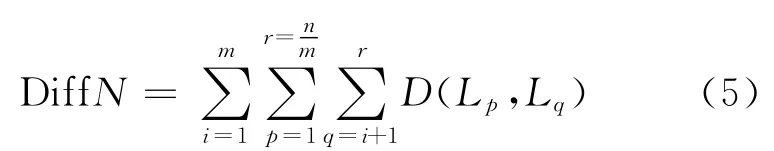
组间差异是各组向量取得均值后，各组各自差异求和，公式为：

适应度函数定义为组内差异与组间差异的比值：

最后进行归一处理，让适应度函数在0到1之间。

2.3 遗传算法操作

遗传算法操作有选择、交叉和变异，初始设定交叉概率为95%，变异概率为5%。一般的选择算子有“轮盘赌选择”、“排序选择”、“最优个体保存”和“随机联赛选择”，文中采用轮盘赌选择。选择概率等于个体适应度值与总适应度值的比例。每次转动圆盘待圆盘停止后指针停靠扇区对应的个体为选中的个体，选择复制它成为子代个体。显然，个体在圆盘中所占的面积越大，其被选中的机会也就越大。

交叉算子是遗传算法中最重要的遗传算子。这里的交叉不是个体与个体的基因交叉，而是个体内部间的交叉，即将个体中的学号交叉互换，以保证每组人数相同，避免重复分配。各组组长的学号位置保持不变，个体后面相邻位置两两搭配成对，对每一对用随机生成的概率与交叉概率比较，若小于交叉概率则交换学号，交叉体现了信息交换的思想。

变异算子是随机生成一个概率，若小于变异概率，进行变异。随机生成两个位置（组长位置除外），将学生的学号进行互换，遗传算法中变异发生的概率很低。变异为新个体的产生提供了机会。

上述操作按顺序进行，每操作一次得到一个新的种群。每次循环通过3种操作后生成k个子代。子代与父代共2k个个体，采用竞争策略，取适应度函数值大的k个个体保留作为下一代，进行循环迭代，当满足结束条件时算法结束。

2.4 收敛条件

终止结束有两个条件：由小到大排序的适应度函数中，后60%的适应度值基本保持不变，或小于差异值θ；到达限定的最大迭代次数。

2.5 算法描述

步骤1：初始化遗传算法中的各个参数，给出总人数n和要分的组个数m（只考虑n%m＝0情况），初始种群数量k、交叉概率Po、变异概率Pb、差异阈值θ、最大迭代次数gmax，建立初始种群P1。

步骤2：计算种群P1中每个个体的适应度值Fi（i＝1，2，…，k），并按降序排列，取适应度大的前k个个体作为新的种群，如果满足终止条件，则终止。

步骤3：执行基本遗传算法的选择、交叉（Po）、变异（Pb）操作，产生k个后代，得到新群体P2，存入下一代中。

步骤4：P1＝P1，转步骤2。

算法以迭代的方式重复执行，迭代一定次数后，种群中的很多个体都具有很强的适应度，适应度最强的一个个体就是我们认为最合理的分组序列，将此个体按照顺序转换一个m×n的矩阵，所在列表示具体某个学生，所在行表示此学生被分到的组。

2.6 实验结果与分析

算法在以下两方面进行了优化：对初始种群进行了优化，减少了迭代次数，提高了收敛速度；组长选出位置后在个体左侧不参与遗传运算，减少了运算量。

为验证此算法，文中随机选取了软件10－1班作为研究对象。布置了一个任务“做一个门户网站，内容、风格、技术都不限，要求组长展示作品时上交完整的协作记录，包括各成员的具体任务及完成情况、小组讨论记录和组长点评，为期一个月”。此次任务采用遗传算法进行分组，与以往档案中最近一次该班级任务记录进行对比。为保证具有可比性，教学模式保持不变，各组组长人员不变。考虑到任务内容不同，只从“小组协作能力”方面给出了分值进行对比，见表1。

表1 成绩对比表（每一项满分为100）

评价分组优劣的一个重要指标就是看小组的协作能力[8]，每组的组员都应通力合作将任务完成。各小组应保证每组的组员参与度大体相当，避免出现“组内任务一人扛”的局面，这正是分组提倡的“组间同质”。试验中，组员由原来的自由分组变成了利用遗传算法分组，可以看出，本次任务协作成绩比较均衡，且普遍高于以往。以往任务虽然有个别小组分值很高，但从“提升全班整体协作能力”角度看没有经过遗传算法分组的教学效果好。

3 结 语

利用遗传算法自动分组，可以合理、快速地分配人员。同时能够注意到，必须有相应的学生个人特征库做支持，这就要求对学生进行合理多方面的特征测试并不断更新，所有老师在进行分组活动时应给予及时记录并进行小组和组员评价，学生个人特征数据库的建立有待进一步建设和完善。

[1]黄荣怀.关于协作学习的组态结构模型研究[C]／／2001全球华人资讯与教育会议.台湾：[出版者不详]，2001.

[2]杨友林，丁硕.基于模糊C均值算法的协作学习分组系统研究[J].电子科技，2009，22（5）：84－86.

[3]李杰，王臧伟，李克东.协作学习中协作小组分组系统的设计与开发研究[J].华南师范大学学报，2007（3）：62－68.

[4]张春玲.基于遗传算法的协作学习自动分组[J].中国信息技术教育，2011，19：67－69.

[5]周明，孙树栋.遗传算法原理及应用[M].北京：国防工业出版社，1999.

[6]郭海湘，诸克军，刘涛.基于 MATLAB采用遗传算法确定最优聚类数目[J].长春工业大学学报：自然科学版，2004，25（1）：12－14.

[7]王婷婷，吴庆麟.学习风格理论综述及其教育启示[J].宁波大学学报：教育科学版，2006，28（4）：47－50.

[8]谢舒潇，黎景培.网络环境下基于问题的协作学习模式的构建与应用[J].电化教育研究，2002（8）：44－47.