用蒙特卡罗法求解贝特朗奇论

段棂宴，王凡彬，2*，杨 进，王鹏程，刘绪涛

（1．内江师范学院数学与信息科学学院，四川内江 641100；2．四川省高等学校数值仿真重点实验室，四川内江 641100）

用蒙特卡罗法求解贝特朗奇论

段棂宴1，王凡彬1，2*，杨 进1，王鹏程1，刘绪涛1

（1．内江师范学院数学与信息科学学院，四川内江 641100；2．四川省高等学校数值仿真重点实验室，四川内江 641100）

针对贝特朗奇论所涉及的一个几何概率问题，由于3种不同样本空间的确定导致其结果的差异，利用蒙特卡罗法随机模拟抽样来验证了解法3的合理性，借助计算机用Matlab软件编程以及数理统计中的统计计数等方法解决了该问题。不仅合理运用了蒙特卡罗法原理，而且对理解以及进一步认识几何概率问题中的随机性具有重要意义。

贝特朗奇论；蒙特卡罗法；概率；统计

蒙特卡罗方法又称统计模拟法、随机抽样技术〔1-4〕，是一种随机模拟方法，是以概率和统计理论方法为基础的一种计算方法，是使用随机数（或更常见的伪随机数）来解决很多计算问题的方法。它将所求解的问题同一定的概率模型相联系，用电子计算机实现统计模拟或抽样，以获得问题的近似解。为象征性地表明这一方法的概率统计特征，故借用赌城蒙特卡罗命名蒙特卡罗方法。它的解题过程可以归结为3个主要步骤：构造或描述概率过程；实现从已知概率分布抽样；建立各种估计量。

蒙特卡罗法即是随机模拟法，运用于解决大量重复随机试验的问题，蒲丰投针问题就是该方法的典型运用，求出了的近似值〔3〕，即是试验中所获得的频率。在贝特朗奇论〔1〕中，3种情况下所求出的概率不同，具体求法过程参见文献〔1〕，本文用蒙特卡罗法进行随机模拟，通过计算机Matlab编程进行了该试验，得到的相应频率与文献〔1〕第三种解法相一致，从而肯定了第三种解法，更加赞同第三种解法。

1 贝特朗奇论

贝特朗奇论：在一圆内任取一条弦，问其长度超过该圆内接等边三角形的边长的概率是多少？

解法1 如图1由于对称性，可预先指定弦的方向。作垂直于此方向的直径，只有交直径于点与点间的弦，其长才大于内接正三角形边长。所有交点是等可能的，则所求概率为。此时假定弦的中心在直径上均匀分布。

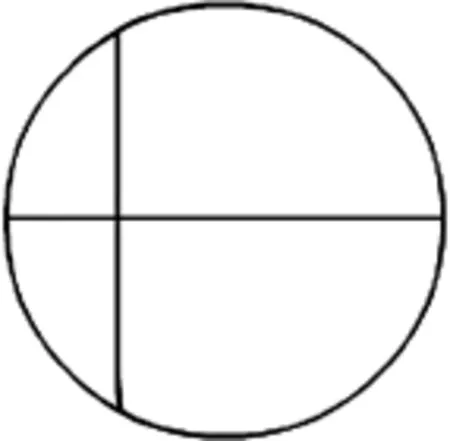
图1 解法1示意图

解法2 如图2由于对称性，可预先固定弦的一端。仅当弦与过此端点的切线的交角在60°～120°之间，其长才合乎要求。所有方向是等可能的，则所求概率为。此时假定端点在圆周上均匀分布。

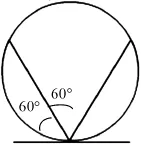
图2 解法2示意图

解法3 如图3弦被其中点位置唯一确定。只有当弦的中点落在半径缩小了一半的同心圆内，其长才合乎要求。中点位置都是等可能的，则所求概率为。

图3 解法3示意图

针对这3种解法，我们认为：由于样本空间选取的不同，解法1、解法2、解法3的结果出现了差异。解法3对样本空间的选取比较自然，符合人们的认知规律，下面我们用蒙特卡罗法来验证这一点。

2 用蒙特卡罗法求解贝特朗奇论

为方便起见，我们在单位圆内接等边三角形上进行讨论。根据问题引入，可先设圆为单位圆，再作其内接等边三角形，可求得等边三角形的边长为，如下图4。

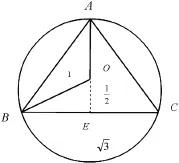
图4 蒙特卡罗法求解示意图

在圆O中，过圆心O作弦BC的垂线于E，因为△ABC为等边三角形，圆心O为三角形的重心，所以OB平分∠ABC，∠OBC=30°，而半径OB=1，所以OE=（在Rt△OBE中，30°角所对的边是斜边的一半），所以BE=，BC=，所以等边三角形边长为（垂弦定理）。

贝特朗奇论中由于3个样本空间的取值不同，导致3种情况下的结果不同，解法1是直径上的点组成的样本空间Ω1；解法2是圆周上的点组成的样本空间Ω2；解法3是大圆内的点组成的样本空间Ω3，其值更满足概率的随机性，下面应用蒙特卡罗法通过一系列的编程，运算并证实解法3的合理性。

根据上一节的解答过程得：可在坐标中取以（0，0）为圆心，半径为1的圆，在圆上任取点（xi，yi），i=1，2，3，4，…，n，任意两点之间的距离即为弦长，要使得弦长超过内接等边三角形的边长即超过。

取任意两点（x1，y1），（x2，y2），连接两点成弦，其中点为要使得弦长超过，即圆心（0，0）到中点的距离d≤。根据此思路运用相关文献〔5-10〕中的知识进行下面的编程。程序如下。程序编写的流程图如图5。

图5 程序编写流程图

表1 程序运行结果

3 结论

本文运用蒙特卡罗法研究了贝特朗奇论，保证了画弦的随机性，通过计算机Matlab编程实现了随机投点，取点和统计，其结果是真实的，有效的。在贝特朗奇论中解法3的弦的选取具有真正意义上的随机性，其答案是合理的，正确的。本文第二节实际通过概率的频率定义来验证了贝特朗奇论中解法3的合理性和正确性，在概率研究和计算机运用方面有一定的见解，对其他概率问题研究有一定的借鉴意义。

〔1〕峁诗松，程依明，濮晓龙．概率论与数理统计教程〔M〕．2版.北京：高等教育出版社，2011．

〔2〕罗伯特．蒙特卡洛统计方法〔M〕．北京：世界图书出版公司，2009．

〔3〕何光．用蒙特卡罗方法计算圆周率的近似值〔J〕．内江师范学院学报，2008，23（4）：2-3．

〔4〕陈作清．关于贝特朗奇论的新见解〔J〕．西北民族大学学报：自然科学版，1998，20（1）：4-6．

〔5〕王欣．MATLAB在图像处理中的应用〔J〕．内江师范学院学报，2007，22（2）：3-5．

〔6〕薛山．MATLAB基础教程〔M〕．北京：清华大学出版社，2011．

〔7〕于丽妮．基于matlab的蒙特卡罗定积分的实现〔J〕．辽宁大学学报：自然科学版，2012，39（2）：1-3．

〔8〕王丙参，魏艳华，张云．蒙特卡罗方法与积分的计算〔J〕．宁夏师范学院学报，2012，33（3）：4-5．

〔9〕杨建．蒙特卡罗法评定测量不确定度中相关随机变量的MATLAB实现〔J〕．计测技术，2012，32（4）：3-4．

〔10〕董世君，薛玮，董爱芹等．Matlab与Excel接口技术在电力系统数据分析中的应用〔J〕．微型机与应用，2012，31（18）：2-3．

Using the Monte Carlo Method to Solve the Bertrand Odd

DUAN Lingyan1，WANG Fanbin1，2*，YANG Jin1，WANG Pengcheng1，LIU Xutao1
（1.College of Mathematics and Information Science，Neijiang Normal University，Neijiang,Sichuan 641100，China；2.Key Laboratory of Numerical Simulation in the Sichuan Province College，Neijiang,Sichuan 641100，China）

This paper is designed to solve the geometric probability problem of Bertrand paradox by using Monte Carlo method.Owing to the result differences which are caused by three different samples space,Monte Carlo method is used to simulate random sampling to verify the rationality of third method.And with the help of the computer,Matlab software programming and mathematical statistics in the statistical counting method are used to solve this problem.This solution is not only using the Monte Carlo law principle reasonably,but also important to understand and know more of the randomness of the geometric probability problem.

Bertrand odd theory；Monte Carlo method；probability；statistics

O211.9

A

1672-2345（2013）04-0009-03

内江师范学院2012年大学生科研基金资助项目（12NSD-40）

2012-12-25

2013-01-08

段棂宴，内江师范学院数学与信息科学学院本科生.

（责任编辑 袁 霞）

10.3969/j.issn.1672-2345.2013.04.004

*通信作者：王凡彬，教授.