基于聚类与均匀分布的图像显著性检测算法研究＊

宋 平，刘 恒

（西南科技大学 信息工程学院，四川 绵阳 621010）

人类视觉系统对视觉场景中感兴趣区域的抽取是一个视觉注意机制显著性检测的过程[1]。在图像理解的同时若能模拟人类视觉机制提取出图像中显著性区域，将会很大程度上提高图像理解的效率。目前，图像的显著性检测已经广泛地运用到许多计算机视觉的应用领域中，如目标检测、场景渲染和视觉界面设计等。

近年来，随着研究的深入，研究者们提出了各种图像显著性区域检测算法。最早的ITTI L等人[2]提出了一种模拟生物视觉注意机制的算法，目前只适用于自然图像。针对Itti模型的不足，田明辉[3]提出一种适用于自然场景的视觉显著度模型，在此基础上结合模糊区域增长方法进行显著性检测。对于不可预知以及复杂场景图像，Hou Xiaodi等[4]和 Guo Chenlei等[5]利用图像频域的统计特性 （如对数幅度和相角）来衡量图像显著性。GOFERMAN S等人[6]提出了一种基于上下文的显著性检测机制，效率比较低。黄志勇等人[7]在参考文献[6]算法基础上进行改进，提出了随机的显著性检测算法，旨在提高显著性检测的速度。

显著性检测的最终结果即检测出人们感兴趣的目标区域，而图像的聚类分析通常依据相似性和相邻性构造分类器，可以将数据对象分割为不同的类。理论上，图像聚类算法可以分割出图像中的前景部分，而人们的感兴趣区域一般也隶属于图像中的前景。因此，可以在进行显著性检测算法之前对图片应用图像聚类算法以实行粗检测。

本文提出了一种新的基于图像聚类与均匀分布的显著性检测算法。在该算法中，首先用图像聚类算法（如K-均值聚类[8]、金字塔聚类[9]和均值漂移聚类[10]）对图片进行粗检测；然后用均匀查找方法检测出聚类后的图像的每一层的粗糙的显著性区域；再采用滤波方式精化粗糙的显著性区域；最后将每层精化了的显著性区域图进行合并。大量实验结果表明，该算法与已有方法相比，准确性明显提高，与人类视觉注意机制较为一致。

1 图像上下文显著性检测原理

基于上下文的显著性检测机制主要依赖于两个定理。

定理1 设两个向量化了的图像块pi和pj在Lab颜色空间的欧氏距离为 dcolor（pi，pj），将其 归一化到[0，1]范围内。当 dcolor（pi，pj）相对于任意的图像块都大时，则像素i是显著的。

定理2 设两个向量化了的图像块pi和pj所在位置之 间 的 欧 氏 距 离 为 dposition（pi，pj）， 将 其 归 一 化 到[0，1]范围内。

基于定理1和定理2，两个图像块的非相似性测量的方法为：

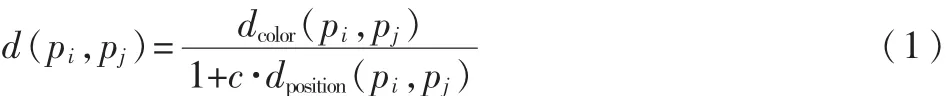
对于每一图像块 pi，依据式（1）找出 K个最相似的图像块，再根据式（2）计算每个像素显著性值：

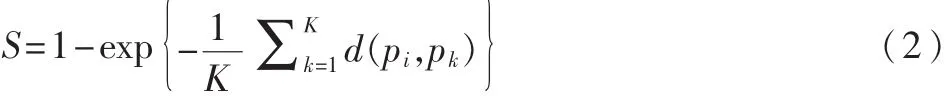
此种显著性检测方法计算量大、效率低，通常只针对于处理规格较小的图片。参考文献[7]提出了一种致力于改善检测速度的随机显著性检测算法：随机地从图像中选取2K个图像块，并且只考虑K个最相似的图像块；采用金字塔分层，并使用8邻域方法对粗糙显著性图进行精化。

[7]算法计算量明显减少，但由于其算法中2K个图像块的随机选取，导致显著性检测效果不太稳定，噪声影响较大，一些检测结果如图1所示。从图1可以看出显著性检测效果不佳，噪声影响较大。基于此，本文考虑从两方面对其进行改善：（1）采用均匀分布，兼顾图像全局信息；（2）采用聚类算法进行图像区域显著性聚类，提高检测的稳定性，避免噪声影响。

2 基于聚类与均匀分布的显著性检测算法

本文算法的主要步骤是：首先利用聚类算法对输入图像进行聚类，突出图像的感兴趣区域，在此基础上进行均匀采样显著性检测，再用双边滤波对粗糙显著性图进行精化。算法总体流程如图2所示。

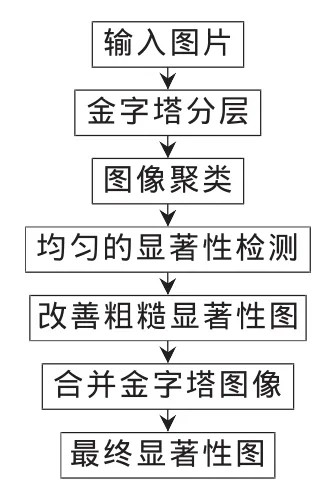
图2 本文算法总体流程

算法的具体描述如下：

（1）金字塔分层

因对单层图片进行计算，显著性检测效果较差，所以有必要先对输入图像进行金字塔分层。一幅图像的金字塔[11]是一系列以金字塔状排列的分辨率逐步降低的图像集合，如图3所示。金字塔底部是待处理图像的高分辨率表示，而顶部是低分辨率的近似。当金字塔向上层移动时，尺寸和分辨率逐步降低。

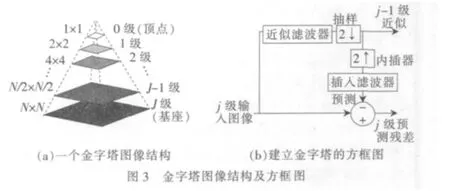
（2）图像聚类

图像聚类能突出图像的显著性区域，去除噪声影响，能给后续的显著性检测工作提供一个较好的粗测基础。本文首先采用金字塔聚类、均值漂移聚类和K-均值聚类3种聚类方法对图像进行聚类计算。均值漂移聚类的聚类效果很明显，能比较准确地分离出前景背景，得到本文想要的图像中的感兴趣区域，因此本文选取均值漂移聚类算法对图像进行粗检测。

均值漂移算法是一种基于核函数估计的无参数迭代算法，其基本原理为：设X为d维空间总体，n个对象Xi（i=1，…，n）为其样本，则 X的核密度函数估计为：

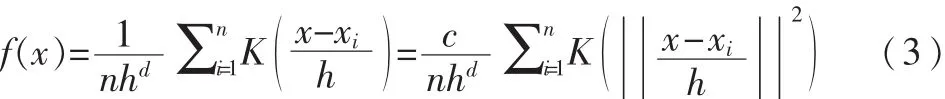
其中，h 为带宽，K（x）=ck（‖x‖2）为核函数。 则核密度梯度▽f（x）=0的模式点为：

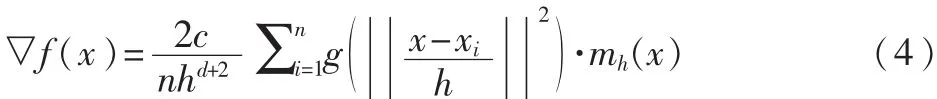
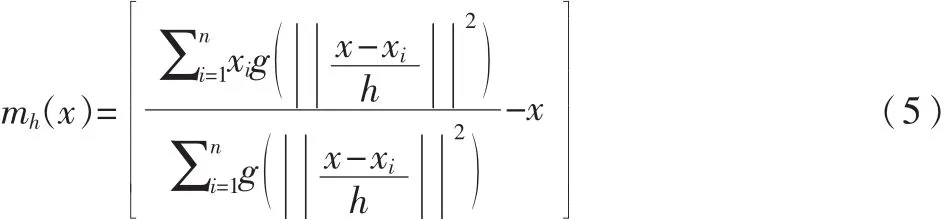
其 中 ，g（s）=-k˙（s），第 一 项 正 比 于 核 函 数 G（x）=cg，dg（‖x‖2）的密度估计，第二项为均值偏移向量。此过程通过迭代 xt+1=xt+mh（xt）实现。

（3）基于均匀分布的显著性检测

在对图像进行聚类后，在此基础上进行基于均匀分布的显著性检测。本文首先将图像均匀地分成2K个图像块，然后找出每个图像块的质心像素点，如此获得图片中均匀的2K个像素点。具体算法为：假设将一幅图像分成2K=N×M个图像块，则每个图像块的中心像素点的坐标值为：

其中，x为横坐标值，y纵坐标值，w和 h分别为图像的宽和高，n=i（i=0，…，M-1），0≤j≤2K。每当 j大于等于N的倍数时，n自增1。

本文实验中，设置c=3。在这2K个候选点之中，依据式（1）计算侯选点与点 i的非相似性；之后只保留2K个像素点中K个相似性值最大的像素点，舍弃其他图形块；再根据式（2），利用 K个相似性值大的像素点计算像素i的显著性值。由于这2K个图像块只是图像中所有图像块中的一小部分，因此会使显著性检测结果存在一定的误差，但是随着K值的增大，即采样数量增加，显著性检测结果的误差会随之减小，当然这样的代价就是实验速率相对缓慢。

（4）改善粗糙显著性图

为同时兼顾良好的实验效率以及较为精确的显著性检测结果，在均匀的显著性检测中，本文仅仅设定K=32。显然，这样一种不完全采样行为会使检测结果存在大量噪声，也就是说像素点的采样量严重不足会给显著性检测带来误差。为解决这个问题，本文引入了双边滤波器来减少噪声。

（5）合并精化显著性检测图

利用金字塔分层进行显著性检测图的合并。在第i层的坐标p处，改善了的显著性值为且 被 归 一 化到了[0，1]。为了计算在第i层中合并了的显著性值，第i-1层的粗糙显著性图被缩放到了与第i层中显著性图一致的尺寸。表示在缩放了的显著性图中位置 p 处的显著性值。这样，相邻两层改善后的显著性图的合并方法如下：

至此，合并后的显著性图已经比较精细，可以用于一些基本的图像应用。

3 实验结果分析及讨论

本文使用VSC++程序设计语言在Windows XP系统环境下实现算法，机器硬件配置为：双核的CPU E6300 CPU，2 GB内存。实验在Achanta等人提供的公开测试集上进行算法测试，此测试集是此类数据最大的测试集，并且已由人工精确标注了显著性区域，实验过程中设置图像尺寸规格为 640×480。

3.1 显著性检测过程中不同参数的分析比较

3.1.1 图像聚类的实验结果分析

图4是对图像分别用3种图像聚类方法进行聚类后的实验结果。实验结果表明，均值漂移聚类算法得到的聚类效果中，图像的前景和背景分离较为彻底，突出的前景与人的主观意志最为一致，而其他两种算法得到的聚类效果则相差太远，不利于进行后续的显著性检测。本文最终选取的聚类算法为均值漂移聚类算法，其能给后续的显著性检测工作提供一个较为准确的人们感兴趣的粗检区域。

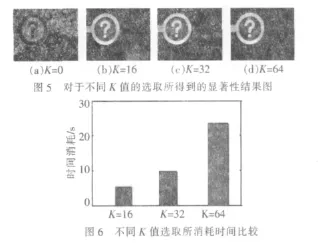
3.1.2 选取不同均匀块K值的实验结果分析

图5和图6表明，K的不同取值将导致不同的显著性检测质量和检测效率。当K=16时，显著性检测质量受噪声影响较大，随着K值的增大，噪声影响逐渐减少，但作为代价，其检测效率将逐渐降低。本实验取K=32，在保证图像的显著性检测效率的同时保证了其显著性检测质量。

3.2 本文方法与其他显著性检测算法的实验结果比较

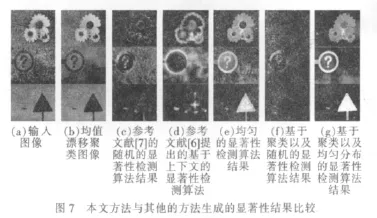
为了分析和验证本文提出的基于聚类以及均匀分布的显著性检测算法的实际效果，本文同时采用了参考文献[7]的随机的显著性检测算法、参考文献[6]的基于上下文的显著性检测算法、均匀的显著性检测算法、基于聚类以及随机的显著性检测算法进行比较，实验结果如图7所示。

图7表明，均匀的显著性检测结果与参考文献[6]和参考文献[7]的检测结果相比更加精细，更加能突出感兴趣区域，只是还存在少量噪声；基于聚类的随机的显著性检测结果与基于均匀分布的显著性检测结果相比，部分图像最后显示不出检测结果，而能显示出检测结果的图像与均匀的显著性检测结果相比，去掉了大部分噪声，这点归功于聚类算法。基于此，本文提出的算法将聚类以及均匀分布相结合，在此基础上进行显著性检测。从图7（g）可以看出，本文算法得到的显著性检测结果明显优于其他4种算法的检测结果，在去掉了大部分噪声的同时还能保证显著性区域的清晰存在，较符合人类视觉注意机制。

从时间消耗这一因素来说，本文的算法也明显优于参考文献[6]的算法。在随机的显著性检测算法以及本文算法中，图像块的采样量比较少，加速了程序运行的速度。而参考文献[6]的算法是利用全部的图像块来进行像素显著性值的计算，计算效率非常低下。此外，均匀的显著性检测与随机的显著性检测算法相比，时间消耗明显减少许多，这是由于随机的显著性检测算法中，图像块需要按照一定的规则去逐个寻找，这个过程需耗费一定的时间，而均匀的显著性检测算法中，图像块是固定的，省去了查找图像块的时间。最终各算法的时间消耗如图8所示。

3.3 关于显著性检测结果稳定性的结果讨论

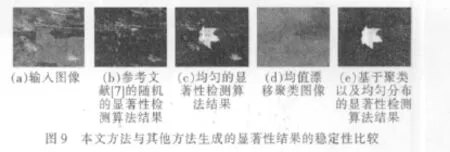
显著性检测结果的稳定性源于整个检测过程中图像聚类和图像块的选取方式两个关键步骤。先对图像用聚类算法进行粗检测，可以很好地去除图像中的背景信息，保留前景部分中感兴趣的区域；然后将图像均匀进行分块，选取每个图像块的中心像素点，如此获得2K个图像块，这将避免随机的显著性检测中出现的情况，兼顾图像的全局信息，因此其显著性检测结果较为稳定。结合聚类算法能更好地去除图像中的背景信息，加强了最终的检测结果的稳定性。本文算法与其他算法生成的显著性结果稳定性比较如图9所示。

大量实验表明，本文提出的基于聚类以及均匀分布的显著性检测算法能得到一个比较准确的显著性检测结果，与人类视觉注意机制符合程度较高，这表明本文方法存在较大的价值。在未来的工作中，将进一步致力于研究显著性检测的困难问题——背景复杂图像的显著性检测算法，以进一步获取对图像显著性检测原理的认识。

参考文献

[1]李寅.基于张量分解的视觉显著性算法[D].上海：上海交通大学，2011.

[2]ITTI L， KOCH C， NIEBUR E.A model of saliency-based visual attention for rapid scene analysis[J].IEEE Transactions on Pattern Analysis and Machine Intelligence， 1998， 20（11）： 1254-1259.

[3]田明辉.视觉注意机制建模及其应用研究[D].合肥：中国科学技术大学，2010.

[4]Hou Xiaodi， Zhang Liqing.Saliency detection： a spectral residual approach[C].Proceedings of IEEE Conference on Computer Vision and Pattern Recognition， 2007： 1-8.

[5]GuoChenlei， Ma Qi， Zhang Liming.Spatio-temporal saliency detection using phase spectrum ofquaternion fourier transform[C].Proceedings of IEEE Conference on Computer Vision and Pattern Recognition， 2008： 116-124.

[6]GOFERMAN S， ZELNIK-MANOR L， TAL A.Contextaware saliency detection [C].Proceedingsofthe IEEE Conference on Computer Vision and Pattern Recognition，2010：2376-2383.

[7]黄志勇，何发智，蔡贤涛，等.一种随机的视觉显著性检测算法[J].中国科学（信息科学），2011，41（7）：863-874.

[8]李翠，冯冬青.基于改进K-均值聚类的图像分割算法研究[J].郑州大学学报（理学版），2011，43（1）：109-113.

[9]JAHNE B.Digital image processing （5rd ed）[M].Berlin：Springer-Verlag，2002.

[10]刘技，康晓东，贾富仓.基于图割与均值漂移算法的脊椎骨自动分割[J].计算机应用，2011，31（3）：760-762.

[11]RAFAEL C G，RICHARD E W.Digital image processing（2rd ed）[M].阮秋奇， 阮宇智， 译.New Jersey，Prentice Hall，2002.