一种基于GPU的图元网状结构DRR并行加速算法
贾晓未,魏 嵬,贾克斌
(1.CSEDepartment,Universityat Buf falo,SUNY14260;2.北京工业大学 电子信息与控制学院,北京 100124)
计算机辅助导航手术(CAS-Computer Assisted Surgery)系统是计算机图像处理及三维可视化技术、机器人技术、空间三维定位导航技术和临床手术等多学科技术结合的产物。其目的主要是借用计算机技术及设备跟踪模拟手术中涉及的每个过程。计算机辅助手术导航系统在骨科创伤手术微创化进程中有着极其重要的意义。计算机辅助骨外科导航手术(CAOS-Computer Assisted Orthopedic Surgery)通过计算机辅助的术前规划,模拟手术,术中追踪手术器械,引导手术以及术后评估,使得骨科创伤手术更安全,更快速,更准确。其中二维三维配准是系统开发中的一项关键技术。目前二维三维图像配准还处于研究阶段[1],还没有稳定的方法可以应用于临床。在现今存在的配准技术中,基于DRR(DigitallyReconstructed Radiograph)的配准方法使用广泛。其中DRR生成也是配准过程中运算时间最长的一个单元,作为配准过程的中间介质,DRR的生成速度和质量往往对配准的效率和精度有至关重要的影响。
目前在实际二维三维配准应用中,除了CT图与2DX 光片直接利用图片信息的配准[2-4],还有很多应用通过植入器件的在3D和2D空间中的配准实现不同维度下的位置匹配[5-6],植入器件的方法由于其较为明显的外部特征在目前的手术应用中也十分常见。不同于CT数据的Volume结构,植入器件往往以网状结构(Mesh)存储,这种结构相比于Volume结构具有空间的不规则性,因此也给DRR的生成带来了很大的难度,传统的方法在遍历时需要消耗大量时间。本文在传统的RayCasting 算法[7-8]基础上,提出了一种基于图元的加速方法,并且给出了针对空间平面与直线的求交问题和光线筛选问题的优化方法。实验结果表明,这一方法大大降低了网状结构DRR生成的时间消耗,同时该方法也具有可并行性。
1 网状结构及传统生成方法
1.1 网状(Mesh)结构
网状结构的数据由众多图元组成,旨在对图元的空间结构进行存储。对于植入器件,图元通常呈三角形状,通过记录三个顶点在三维空间坐标系下的坐标保存每个图元的空间位置。完整的植入模型数据通常由大量的图元组成。
如图1所示,网状结构中每个三角形片层以其顶点A,B,C的空间坐标依次存储,向量AB×AC表示了该平面的法线方向,指向物体外侧。网状结构模型由这样的片层结构组成其表面,通常其内部认为是匀质结构,因此DRR中像素值与对应光线的射入光路距离直接相关。
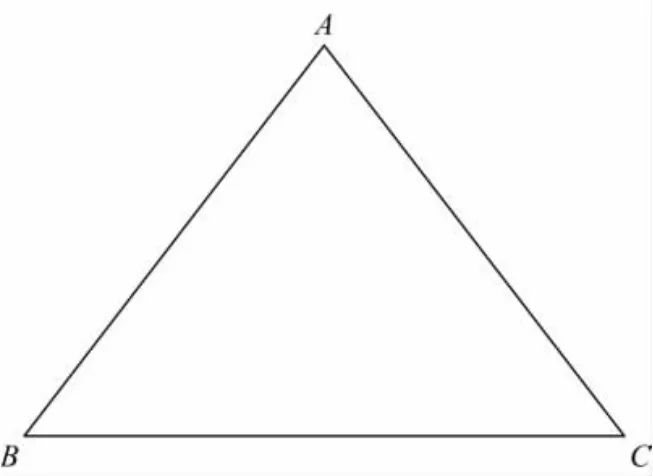
图1 网状结构图元示意图Fig.1 Triang leprimitives tructure
图2为一个植入器件的网状结构模型。对一个匀质结构,通常在保证失真程度较小的前提下将其空间结构以网状形式存储,用网状结构中每个三角形片元顶点的空间坐标记录其空间位置,以此保证整个模型的外表面结构被较为完整地保存。

图2 投影模型示意图Fig.2 Projection Model
1.2 传统方法
传统的Ray Casting算法通过遍历每个像素,并且计算每条由像素投射出的光线被遮挡部分的密度积分,最终合成整幅DRR图像。对于网状结构,与Volume结构不同的是,由于不能根据光线的斜率直接计算出相关的交点,往往需要遍历所有的三角形面,并依次求取交点然后计算积分值,最终合成DRR图像。通过搭建如八叉树等数据结构,可以提升遍历的速度。但是由于网状结构对于投影模型不确定的空间特性,搭建这样的数据结构具有一定的困难。在传统RayCasting算法上,本文将提出一种基于图元的加速算法,很大程度上减少了计算量,且算法具有可并行性。
1.3 投影模型
本文引入一种投影模型,如图3所示。其中UVW为投影模型坐标系,XYZ为数据模型坐标系。Ru,Rv,Rw 表示绕 U,V,W 轴的旋转角,Tu,Tv表示在UV平面内的平移参数,D1,D2分别表示光源距ISO中心和ISO中心距接收屏的距离。对应的转换矩阵为:

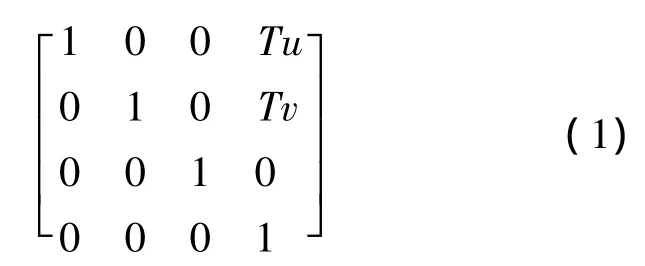

图3 投影模型示意图Fig.3 Projection Model
通过
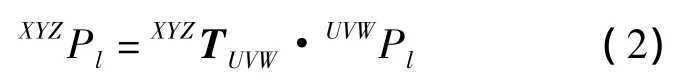
可将UVW坐标系下坐标转至XYZ坐标系。
2 基于图元的加速方法
2.1 方法描述
本文以每个图元,即三角形片作为一个单元,对于由像素投射出的光线进行遍历,计算光线与三角形平面的交点并记录在以光线序号为下标的结构中,完成所有图元的计算后通过每条光线的积分值合成DRR图像。
实际的植入器件往往由大量图元片层构成,因此基于图元的算法具有更强的并行性。在另一方面,对于某一三角面图元,可以通过光源与接收屏的位置进行光线筛选,缩小需要遍历的光线范围,进而很大程度上减少了每个图元的计算任务量,算法过程如图3所示。

图3 基于图元的Ray Casting方法Fig.3 Primitive-based Ray Casting Method
由于真实数据中图元数量较大,因此图3中第一个对于图元的遍历可以通过硬件并行计算,能够显著减少时间消耗。对于光线范围的筛选,首先将三角面三个顶点坐标进行式(2)的逆变换,由XYZ坐标系转换至UVW坐标系,然后在UVW坐标系下计算由光源,即(O,O,Dl)点发出的经过这三个顶点的三条直线与平面W=-D2,即接收屏的交点,分别取这三个交点在U方向和V方向上的最小值和最大值,以此得到所需遍历的光线的最小矩形范围区域。
2.2 空间中求交点的优化方法
在网状结构生成DRR的过程中,核心问题在于判断空间中直线是否与三角面相交,并且计算交点。处理这个问题消耗的时间将直接影响整个算法的效率。
实际应用中往往通过先求直线与三角形所在平面的交点,再判断该交点是否位于三角形平面内。由于判断同一平面中的一点是否位于三角形内相对容易,因此这种方法也被广为接受。然而,由于网状结构中存在大量十分微小的三角面,而且光线数目众多,因此这种方法往往在计算交点上花费了过多的时间。
本文采用类似文献[9]的方法求解空间三角面与直线的交点。首先以

分别表示空间三角面与直线,式中:(u,v)为一点在三角形内重心坐标系下的坐标;O为光源点;D为步长。联立方程(3)和方程(4)有
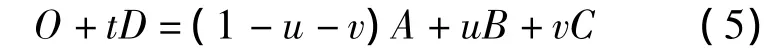
整理后得

由克莱默法则,有

式中:E1=B -A,E2=C -A,T=O -A,P=(D ×E2),Q=(T×E1)。交点在三角形内的充要条件为 u≥0,v≥0,u+v≤1。
为了对光线的积分值进行计算,需要判断光线对于该三角面为入射状态还是出射状态。在1.1节中提到,E1×E2表示法线方向,并指向物体外侧,因此通过判断(L=D·(E1×E2))是否大于0来确定出射点和入射点,可以得到入射或出射的信息。
在图3中最后对于光线的循环中,当按序排列的交点列中相邻的两点依次为入射和出射时,将两点间的积分值累加到整条光线的积分值,最终合成整幅DRR图像。此方法计算过程中考虑了一些多次计算的中间变量,同时可以根据变量的值判断三角片元与光线是否相交,若不相交则不用准确计算交点位置,因此相对于传统方法节省了不必要的计算时间。
3 基于GPU的并行加速
基于图元的Mesh DRR生成算法具有较好的并行性,且对于光线的筛选优化可以有效减少每个线程的计算任务量。
在CUDA架构下,显示芯片执行时的最小运算单元是工作线程(Thread)。多个工作线程组成一个块(Block)。多个块又组成一个栅格(Grid)。每一个栅格对应着一个设备程序即Kernel。对于本文中提出的基于图元的网状结构模型DRR生成算法,以针对每个图元的计算量为GPU中的一个线程并行计算。
由于CUDA对资源访问的限制,不同块之间的内存是不能共享的,不同块之间的通信也受到一定限制。由于不同线程对同一像素值进行改写时会发生写冲突,本文中主要采用重启Kernel函数的方法实现线程同步,同时,设定一定容量的暂存空间保存中间结果,以减少重启Kernel函数的次数,进而减少了因重启Kernel函数带来的开销。首先建立以图元编号为下标的结构,在Kernel函数中每个线程将交点信息及光线编号存入对应的位置中,当显存占满时,退出Kernel函数,将数据导入以光线编号为下标的结构中,然后再启动Kernel函数,直至光线遍历结束。这种方法的缺陷在于,两种储存结构的转换需要消耗大量的时间。因此,本文中将这种转换以Kernel函数的形式在GPU中执行,以对目标结构每个光线编号对应的位置进行存储的任务作为一个线程,以此减少时间消耗。
当求交过程结束后,需要进行积分的计算,以每个像素为线程,过程如下:
(1)对交点位置进行排序。
(2)依次判断,当两个相邻的交点分别为入射和出射的状态时,计算两点间积分,累加到该像素的积分值。
(3)若不满足入射出射的状态,则说明该交点位于图像的棱角处,不需要进行累加积分,寻找下一组满足要求的交点。
4)每个线程判断完所有的交点得到最终每个像素的积分值,合成整幅DRR图像。
改进算法完整流程如图5所示。

图5 改进的MeshDRR算法流程图Fig.5 Improved MeshD RRGeneration Method
4 实验结果与比较
所用实验数据为图6所示的植入模型的真实样例。
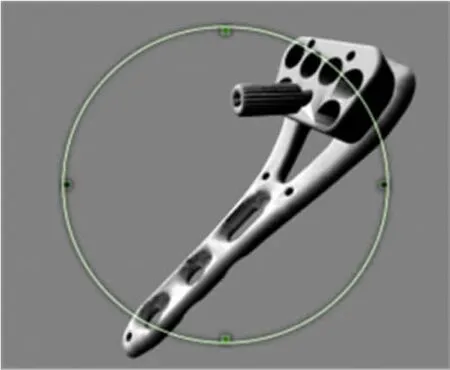
图6 网状结构植入模型示意图Fig.6 Implant Model
实验环境为IntelXeonCPUE5405@2.00 GHz2.00GHz,3.25GBofRAM,显卡 Quadro FX570,显存 256MB。用于实验的程序在WindowXP平台下开发,由 VS2008编写,其中GPU加速部分基于Cuda1.0。数据为35378片的植入模型压缩数据,实验生成DRR图像,图像分辨率为200×250。
以本文算法生成DRR图像如图7所示。

图7 植入模型不同角度DRR生成图Fig.7 DRR of Implant Modelin Dif ferent Views
实验随机产生Ru,Rv,Rw50次,并对时间消耗求平均值。表1为传统算法与改进算法的时间消耗。

表1 传统算法与改进算法的时间消耗Table1 Time Coston Classic Method and Accelerated Methods
由表1可以看出,经过2.2节中所提到的交点求取方法优化后,时间消耗有了很好的改善。由于本文采用了基于图元的方法,因此得以在此基础上针对每个图元做光线的筛选。由表1可以看出,这一步改进对时间消耗的改进更为显著,原因主要在于,在真实数据中,存在大量的光线与图元没有相交。经过GPU加速的算法由于各个线程的并行计算从而使得时间消耗有明显减少。
4 结束语
由实验数据可以看出,这种基于图元大大减少了时间消耗,同时可以保证图片质量。与传统RayCasting的并行性[10]相比,这种方法同样适用于并行运算,以每个图元作为并行计算的线程,另外光线筛选的方法显著降低了每个线程的计算任务量。因此这种方法有其应用价值,同时为基于植入模型的二维三维配准在性能上的提升奠定了基础。
[1]Markelj P,Tomazevic D,Likar B,et al.A review of 3D/2D registration methods for image-guided interventions[J].Medical Image Analysis,2010,16(3):642-661.
[2]Lemieux L,Jagoe R,Fish D R,et al.A patient to computed tomography image registration method based on digitally reconstructed radiograph[J].Med.Phys,1994,21(11):1749-1760.
[3]Penny G P,Weese J,Little J A,et al.A comparison of similarity measures for use in 2-D-3-D medical image registration[J].IEEE Transactions on Medical Imaging,1998,17(4):586-595.
[4]Jacquet W,Nyssen E,Bottenberg P,et al.2D image registration using focused mutual information for application in dentistry[J].Computers in Biology and Medicine,2009,39(6):545-553.
[5]Mohamed R Mahfouz,William A Hoff,Richard D Komistek,et al.A robust method for registration of three-dimensional knee implant models to two-dimensional fluoroscopy images[J].IEEE Transactions on Medical Imaging,2003,22(12):1561-1574.
[6]Mohamed R Mahfouz,William A Hoff,Richard D Komistek,et al.Effect of segmentation errors on 3D-to-2D registration of implant models in X-ray images[J].Journal of Biomechanics,2005,38(2):229-239.
[7]James F Blinn.Light reflection functions for simulation of clouds and dusty surfaces[J].Computer Graphics,1982,16(3):21-29.
[8]Levoy M.Display of surfaces from volume data[D].Chapel Hill,North Carolina:Department of Computer Science,University of North Carolina at Chapel Hill,1989.
[9]Prosolvia Clarus A B,Ben Trumbore.Fast,minimum storage ray-triangle intersection[J].Journal of Graphics,GPU& Game Tools,1997,2(1):21-28.
[10]Ruijters D,Ter Haar Romeny B M,Suetens P.GPU-accelerated digitally reconstructed radiographs[C]//BioMED(08 Proceedings of the Sixth IASTED International Conference on Biomedical Engineering),Canada,2008,601:431-435.

