预应力对体外预应力简支钢梁自振频率的影响

刘寒冰，王龙林，谭国金，程永春，吴昌霞

（1.吉林大学 交通学院，长春 130022；2.长春市市政工程设计研究院，长春 130033）

对于运营期的桥梁，利用现有的方法，是很难对预应力力筋的确切预应力数值进行测试的。自振频率对预应力值具有一定的敏感性，基于桥梁自振频率对有效预应力进行识别是一种有效的方法［1－2］。

传统的观点认为预应力会导致“压缩软化”效应，基于受轴向压力作用的伯努利－欧拉梁动力计算模型推导出的预应力梁自振频率公式的计算结果表明，预应力会导致梁的自振频率减小。然而，在国内外大量预应力简支梁的动力试验中，测试出的梁的固有频率是随着预应力值的增大而增大的，这与经典理论计算结果相反［3-4］。针对此现象，有研究者提出另一种解释：由于混凝土试验梁收缩、梁自重以及随构件一起移动的动力作用而引起混凝土开裂，预应力的作用使这些裂缝闭合，导致梁的中性轴移动，挠曲刚度增大，从而引起梁的基频增大［5-6］。基于这种刚度提高理论和试验数据，国内外研究者们提出了预应力混凝土梁的刚度修正模型［7-8］。虽然通过刚度修正模型计算出的自振频率与试验结果吻合较好，但是刚度修正公式仍然是经验性的，理论支撑不够完备，不具备普遍适用性。

综上所述，至今并未形成确定的桥梁自振频率与预应力值的定量关系［9-10］。本文以此为切入点，同时为避开混凝土梁的开裂对梁自振频率的影响，采用直线布筋的预应力钢梁作为研究对象，利用有限元方法，将其分为钢梁和预应力钢筋两个独立的振动子系统，建立钢梁与预应力筋的耦合振动有限元模型。考虑不同预应力值及预应力筋不同偏心距布置，对预应力钢梁进行动力仿真分析。通过仿真结果分析预应力大小对自振频率的影响规律及影响程度。

1 预应力梁自振频率理论分析

1.1 传统的理论分析模型

传统的预应力混凝土梁自振频率理论分析计算图如图1所示。

图1 简支梁在外部轴向压力作用下的自由振动Fig.1 Free vibration of simply supported beam under external axial compressive force

将预应力作用视为作用在结构上的一对外力，基于平截面假定，建立梁的自由弯曲振动微分方程为

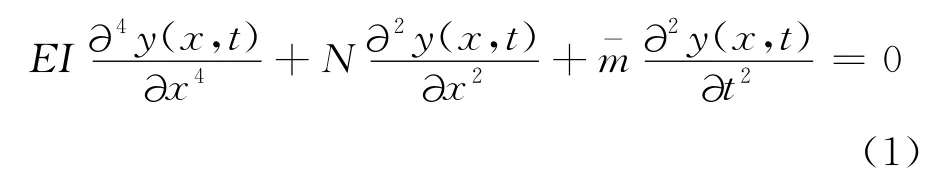
式中：y（x，t）为梁振动时各点的挠度；N为等效轴向作用力；m－为梁的分布质量。

对式（1）进行求解，可得到梁的自振频率为

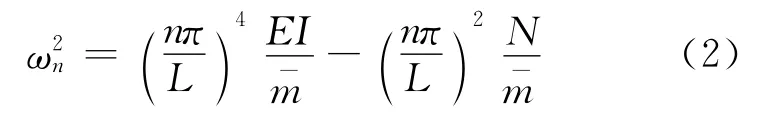
式中：n＝1，2，3，…；EI为梁的抗弯刚度；L 为梁长。

从式（2）中可以看出，梁的各阶自振频率均随着预应力值的增大而减小。此计算公式将预应力视为作用于梁体的外力，而实际上预应力梁是一个自平衡体系。因此，采用此方法计算出的预应力混凝土梁自振频率会存在较大的误差。

1.2 刚度修正模型

为了解释试验中预应力梁自振频率随预应力值增大而增大的现象，Saiidi等［3］通过模型试验，对实测数据进行回归分析，得出主梁刚度的修正式为

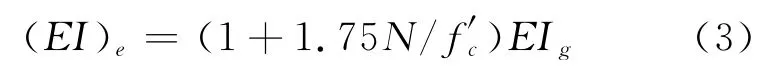
式中：（EI）e为修正后刚度；f′c为自振频率；EIg为修正前主梁刚度。

国内华中科技大学的张耀庭教授［6］针对轴心布置预应力筋的无粘结预应力混凝土梁进行了动力测试，结果表明：轴心作用的预应力值由0变化到88kN，混凝土梁的基频增大9.7%。进行了5根全预应力梁的动力试验，得到了相似的结果：全预应力梁的固有频率随着预应力的增加而增加。为此，根据试验结果，提出了如下的预应力刚度修正公式：

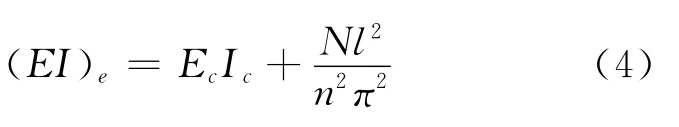
国内多名学者都同样采用试验的方法，得出了多种的预应力混凝土梁刚度计算修正公式。从这些修正公式可以看出，虽然通过刚度修正模型计算出的自振频率可较好地符合试验结果，但是刚度修正公式仍然是经验性的，理论支撑不够完备，不具备普遍适用性。

2 预应力梁动力分析有限元仿真模型

由于经典理论和试验结果存在相反的结论，而现有的理论并不能很好地解释产生这种分歧的主要原因。因此，本文利用有限元方法分析预应力对简支梁的自振频率的影响。在分析中，为避开混凝土梁的开裂对梁自振频率的影响，采用直线布筋的预应力钢梁作为研究对象。预应力钢梁尺寸如图2所示，其中钢材型号为Q345QE，预应力筋采用φs15.2钢绞线，标准强度为1860MPa；锚固处加劲肋厚20mm，其余加劲肋厚6mm；e为预应力筋布置偏心距。建立的钢梁有限元模型如图3所示。

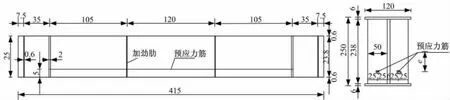
图2 预应力钢梁尺寸Fig.2 Dimensions of prestressed reinforcement

图3 钢梁有限元模型Fig.3 Finite element model of steel beam

在有限元模型中，钢梁采用实体单元，单元类型为SOLID45，钢梁总长4.15m，为工字型横截面，钢材型号为Q345。预应力筋采用link8单元，在钢梁腹板两侧对称布置，共布置2根，单根面积为139mm2，预应力钢绞线标准强度为1860 MPa。预应力筋的锚固及与钢梁的接触采用耦合方法处理。在预应力筋的两个锚固端，预应力筋节点与此处钢梁肋板结点耦合X、Y、Z三个方向自由度（其中Z方向为沿梁纵向）；在预应力筋非锚固端穿过钢梁肋板处，耦合预应力筋结点与肋板结点的X、Y两个方向自由度。采用此模型进行有预应力模态分析。

3 预应力对简支梁自振频率的影响

3.1 预应力值大小的影响

为了分析预应力值大小对钢梁自振频率的影响，采用预应力筋沿梁形心布置的方式，分析不同预应力张拉值条件下的钢梁自振频率。分析结果如表1所示。

由表1可看出，钢梁一阶频率随着预应力值的增大而增大。预应值由0增大到20kN时，一阶频率增了10.03%。因此，即使沿梁截面形心布置预应力筋，其预应力的大小仍对梁的自振频率有比较明显的影响。

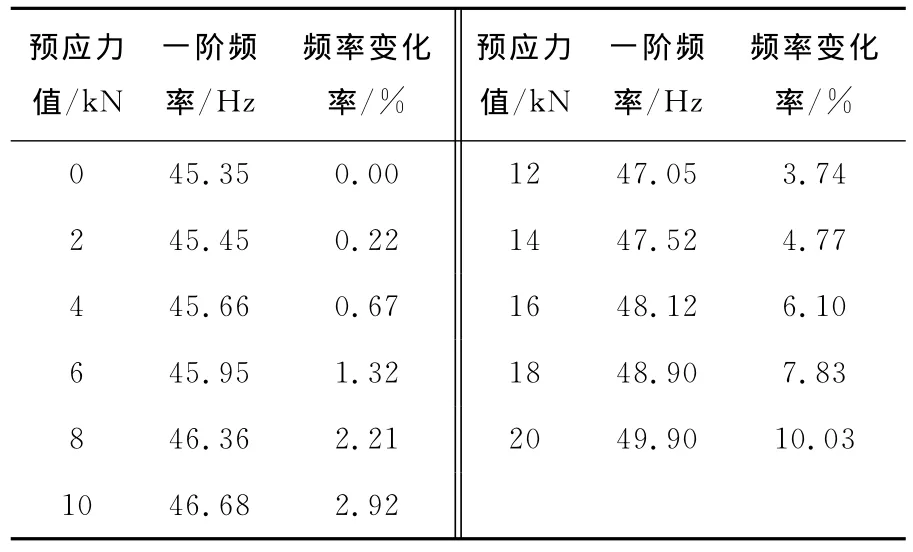
表1 不同预应力值下钢梁一阶频率Table 1 Nature frequency of steel beam under different prestress

为了分析预应力大小对梁自振频率的影响规律，采用最小二乘法对不同预应力值下钢梁基频数据进行拟合，拟合曲线如图4所示。得到了如下钢梁基频与预应力值大小的函数关系：

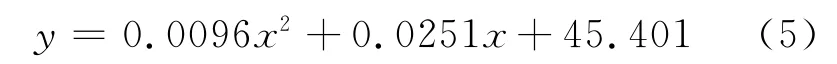
拟合相关系数R2为0.9957，相关性显著，拟合效果良好。由式（5）可以看出，钢梁基频随预应力值的增大呈非线性增大，并非传统理论中的线性减小关系。

图4 不同预应力值下钢梁一阶频率Fig.4 Nature frequency of steel beam under different prestress

3.2 预应力筋不同偏心距的影响

为了分析预应力筋布置位置对钢梁自振频率的影响，建立预应力筋不同偏心布置的钢梁有限元模型，分析其在不同预应力值作用下自振频率。得到的分析结果见表2。

利用表2中的数据，做出钢梁一阶频率随预应力值和预应力筋布置偏心距变化的二元曲面图（见图5），以及相同预应力值条件下钢梁一阶频率随预应力布置偏心距变化的变化图（见图6）。

从图5及图6可看出：在预应力值相同的情况下，随着预应力筋布置偏心距的增大，钢梁一阶频率增大；采用同样的偏心距布置，钢梁一阶频率均随预应力值的增大而增大。

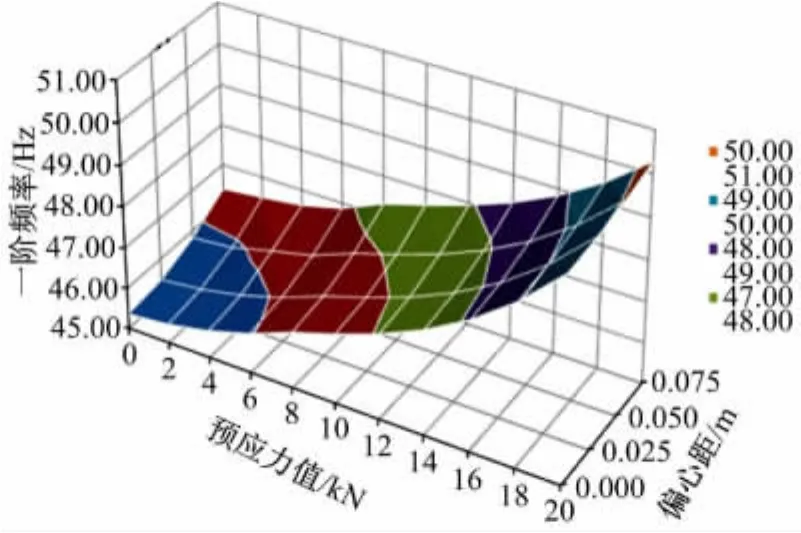
图5 不同预应力值及不同偏心距下钢梁一阶频率Fig.5 Nature frequency of steel beam with different eccentricity under different prestress

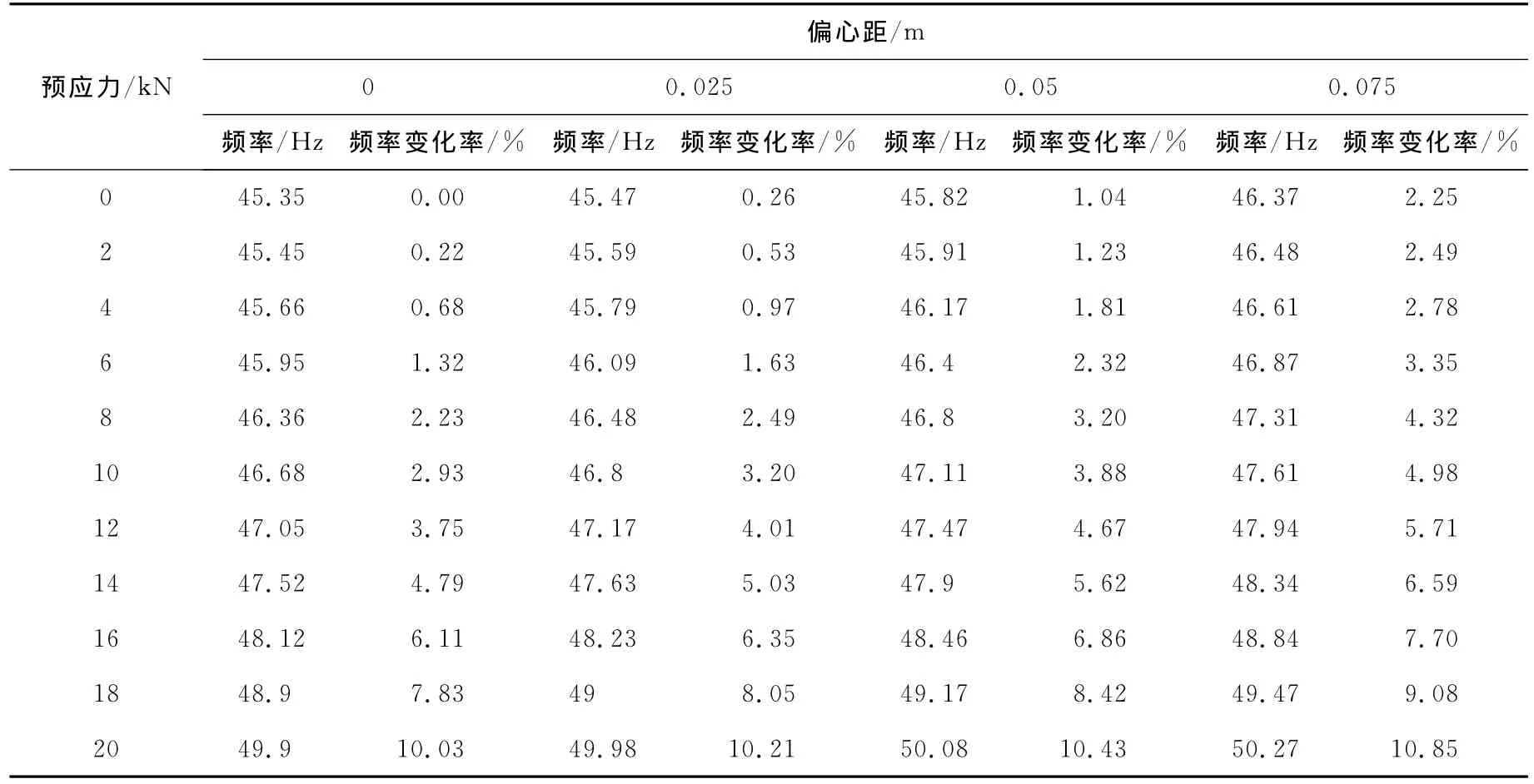
表2 不同预应力值及不同偏心距下钢梁一阶频率Table 2 Nature frequency with different eccentricity under different prestress

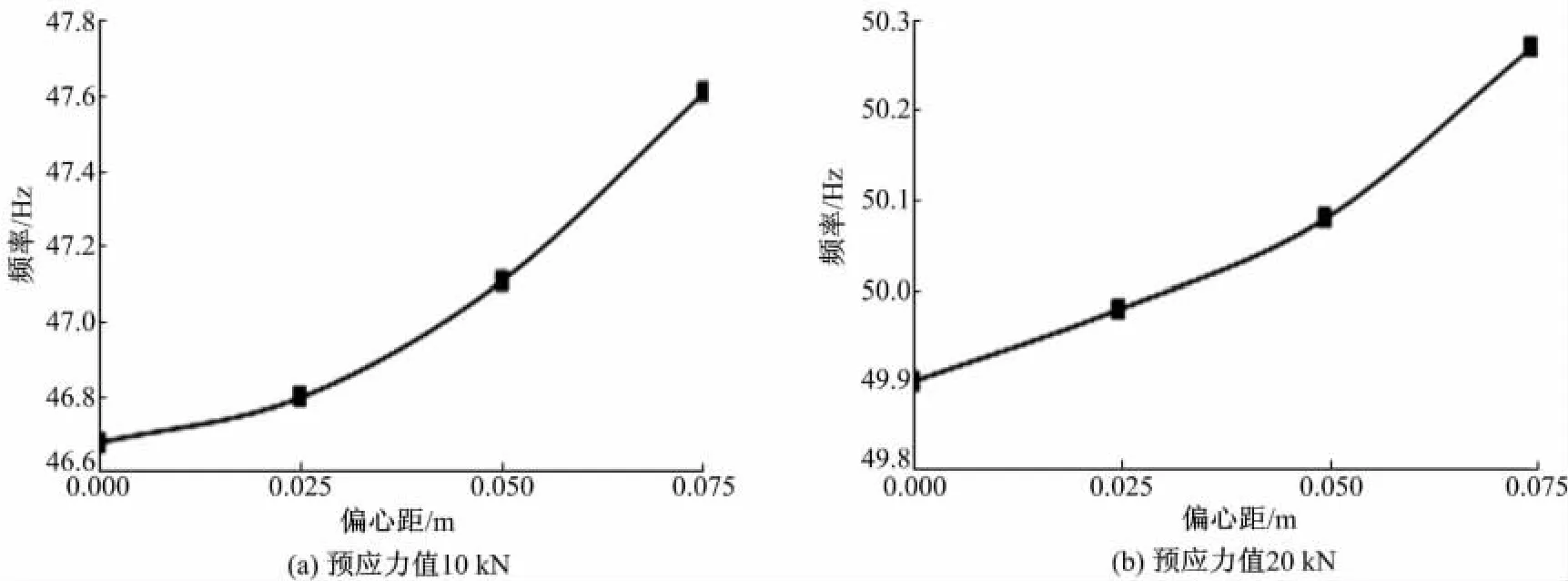
图6 相同预应力值条件下钢梁一阶频率随预应力布置偏心距的变化曲线Fig.6 Change curve of nature frequency with eccentricity of prestressed steel under the same prestress

4 结束语

为了分析预应力对简支梁自振频率的影响规律，本文采用有限元方法，建立不同预应力值和不同预应力筋布置位置下的钢梁有限元仿真模型，对钢梁进行有预应力模态分析。分析结果表明：在沿钢梁截面形心布置预应力筋情况下，钢梁的基频随预应力值的增大呈现非线性增大的关系；采用不同偏心距布置预应力筋情况，钢梁一阶频率均随预应力值的增大而增大；在预应力值相同的情况下，随着预应力筋布置偏心距的增大，钢梁一阶频率增大。因此，利用桥梁自振频率对有效预应力进行识别是可行的，但仍需进行更深入的理论研究。

［1］Kim Jeong－tae，Ryu Yeon－sun，Yun Chung－bang.Vibration－based method to detect prestress－loss in beam－type bridges［C］∥Proceedings of the International Society for Optical Engineering（SPIE），2003：559－568.

［2］Kim Jeong－tae，Yun Chung－bang，Ryu Yeon－sun，et al.Identification of prestress－loss in PSC beamsusing model information［J］.Structural and Mechanics，2004，17（3－4）：467－482.

［3］Saiidi M，Douglas B，Feng S.Prestress force effecton vibration frequency of concrete bridges［J］.Journal of Structural Engineering，1994，120（7）：2233－2241.

［4］李维奇，张耀庭，李进.基于损伤机理的预应力混凝土梁振动频率研究［J］.华中科技大学学报：城市科学版，2009，26（2）：90－94.Li Wei－qi，Zhang Yao－ting，Li Jin.Vibration frequency of pretressed concrete beam based on damage theory［J］.Journal of Huazhong University of Science and Technology（Urban Science Edition），2009，26（2）：90－94.

［5］Jagmoban L H，Ahmed H K.Discussion of prestress force effect on vibration frequency of concretebridges［J］.Journal of Structural Engineering，1995，121（1）：458－460.

［6］张耀庭，汪霞利，李瑞鸽.全预应力梁振动频率的理论分析与试验研究［J］.工程力学，2007，24（8）：116－120.Zhang Yao－ting，Wang Xia－li，Li Rui－ge.Experimental and theoretical research on vibration frequency of full－prestressed concrete beam［J］.School of Civil Eng ＆ Mechanics，2007，24（8）：116－120.

［7］刘龄嘉，贺拴海，赵小星.预应力对混凝土简支梁振动频率影响的试验研究［J］.铁道建筑，2007（8）：10－12.Liu Ling－jia，He Shuan－hai，Zhao Xiao－xing.Experimental research on the effect of the prestress on the vibration frequency of simply supported concrete beam［J］.Railway Engineering，2007（8）：10－12.

［8］刘龄嘉，贺拴海，赵小星.在役混凝土简支梁有效预应力计算［J］.交通运输工程学报，2005，5（3）：47－51.Liu Ling－jia，He Shuan－hai，Zhao Xiao－xing.Calculation on effective prestress of simply supported concrete beam in use［J］.Journal of Transportation Engineering，2005，5（3）：47－51.

［9］谭国金，刘寒冰，程永春，等.基于车桥耦合振动的简支梁桥冲击效应［J］.吉林大学学报：工学版，2011，41（1）：62－67.Tan Guo－jin，Liu Han－bing，Cheng Yong－chun，et al.Analysis of impact of vehicle of simply supported beam bridge based on vehicle－bridge coupled vibration［J］.Journal of Jilin University（Engineering and Technology Edition），2011，41（1）：62－67.

［10］焦玉玲，刘寒冰，秦绪喜，等.权函数对梁自由振动问题计算精度的影响［J］.吉林大学学报：工学版，2008，38（3）：624－629.Jiao Yu－ling，Liu han－bing，Qin Xu－xi，et al.Weight function effects on computational precision of free vibration of beam［J］.Journal of Jilin University（Engineering and Technology Edition），2008，38（3）：624－629.