大跨中承式钢管混凝土拱桥的自振特性及稳定性

云 迪，刘 贺，张素梅

（1.吉林建筑工程学院 土木工程学院，长春 130118；2.吉林农业工程职业技术学院，吉林 四平 136001；3.哈尔滨工业大学 土木工程学院，哈尔滨 150090）

0 引 言

自我国于1990年首次将钢管混凝土作为拱肋用于公路桥梁建设以来，钢管混凝土拱桥发展迅猛，2000年后钢管混凝土拱桥超越钢筋混凝土拱桥和钢拱桥成为中国修建数量最多的拱桥桥型。已建成的跨径在百米以上的钢管混凝土拱桥占56.3%，即已有的钢管混凝土拱桥多属于大跨径桥梁［1］。

钢管混凝土拱桥较大的跨宽比、较小的构件截面尺寸、良好的面内整体性等特点使其面外刚度相对较弱。为了提高钢管混凝土拱桥的面外刚度，改善其结构性能，对桥型及结构参数进行了研究，提出了提篮拱、钢管－钢管混凝土复合拱、单肋斜撑拱等新桥型，确定了拱肋矢跨比、拱肋截面、横撑布置等影响拱桥横向刚度的重要结构参数。对上述结构参数进行研究时，动力特性分析以其快速直观的特点得到重点研究，自振频率及振型作为动力特性分析的重要指标被广泛用于评价结构参数取值的合理性［2-5］。

根据结构动力学原理，结构自振特性仅与结构弹性刚度矩阵和质量矩阵有关，而结构在外荷载作用下刚度降低，结构刚度矩阵发生变化，仅依据自振特性分析结果评定结构参数取值的合理性欠妥。研究钢管混凝土拱桥稳定性的一个常用方法是非线性稳定分析，该方法基于实际构件的失稳属于二类稳定问题，即极值点失稳问题，分析过程中综合考虑结构几何非线性与材料非线性的双重影响，可以更精确地定量反映结构的整体稳定性。由于该方法较弹性分析复杂费时，一般仅用于研究几何非线性和材料非线性对成桥稳定性的影响程度或研究不同拱肋模型对成桥稳定性的影响，很少用于结构参数的讨论［6-7］。

为弥补自振特性分析无法考虑荷载工况对结构刚度矩阵的影响，利用弹性稳定性分析快速省时的优点初步对一360m跨中承式钢管混凝土拱桥的主要结构参数进行讨论；之后综合考虑几何与材料双重非线性的稳定性分析对自振特性及弹性稳定性分析的结果进行验证，研究了矢跨比及拱面内倾角度对结构静动力性能的影响，提出了矢跨比及拱面内倾角的建议取值区间。

1 有限元模型

本文以一座跨度为360m的中承式钢管混凝土拱桥为算例，其为一计算跨径l0＝344m的悬链线无铰拱（拱轴系数m＝2、k＝1.317），矢跨比f／L＝1／4.5［8］。

该算例的主要结构构件包括：六肢桁式钢管混凝土拱肋；圆钢管桁架横撑；间距为8m、极限抗拉强度为fu＝1670MPa的镀锌高强钢丝束吊杆；间距为8m的钢管混凝土立柱；计算跨径为35.95m的工字形截面钢横梁；22cm厚的预制钢筋混凝土桥面板（对于12cm厚的桥面铺装层，只计自重不计刚度）。各主要结构构件的材性及有限元单元类型见表1。钢材及混凝土的相关材料力学性能指标均按照现行结构设计规范取值；拱肋钢管混凝土弦管的组合材料模型及材性依据文献［9－10］确定。文献［10］分别对文献［11－12］的拱肋模型进行了双重非线性有限元分析，并与文献［11－12］给出的试验结果进行了对比，吻合良好。本文依据文献［10］的分析结果，考虑到计算机求解耗费的机时及结果存储空间等综合因素，钢管混凝土拱肋采用双线性随动强化材料模型。

图1为全桥空间有限元模型，其拱脚嵌固；柔性吊杆与桥面系、柔性吊杆与拱肋均为铰接；其他节点为刚接。

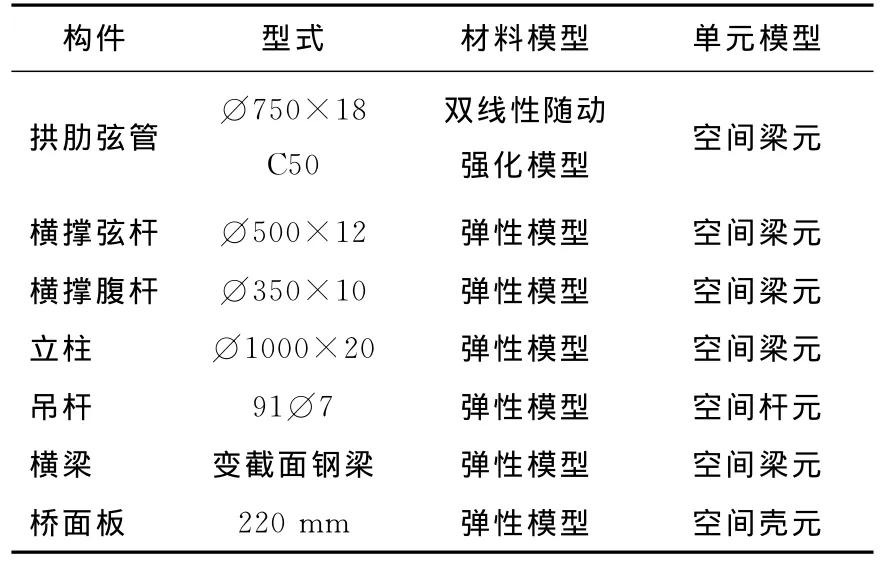
表1 结构构件表Table 1 Structural members

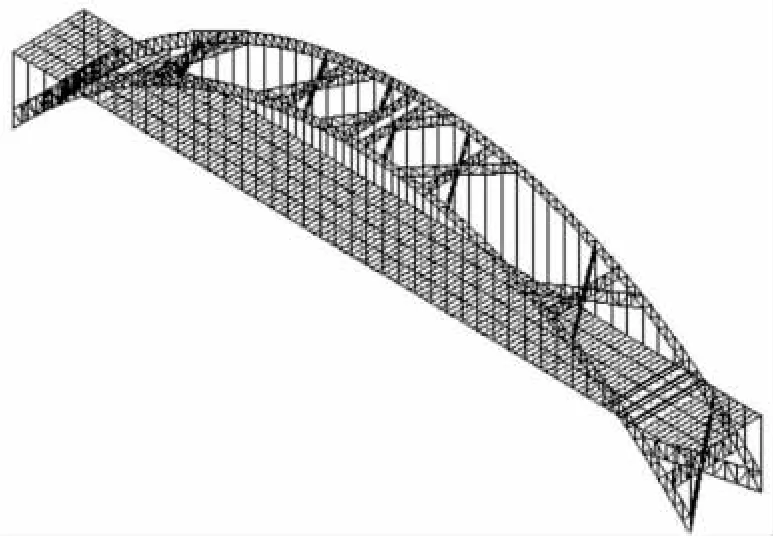
图1 有限元模型Fig.1 Finite element model

2 自振特性及稳定性分析

2.1 自振特性分析

自振特性分析实质是以无阻尼振动为前提求解无外荷载作用时结构的动力平衡方程。假定体系作简谐振动将问题转化为经典的广义特征值问题［13］，即：

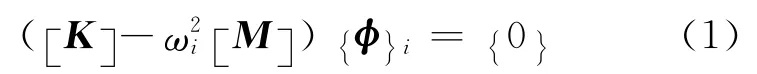
式中：［K］、［M］分别为结构的总刚度矩阵及结构的总质量矩阵。

求解特征方程（1），得到结构第i阶自振频率ωi及相应振动模态的振型向量｛φ｝i。

钢管混凝土拱桥已有动力特性分析表明：一般地，结构前几阶自振频率和振型对结构自振特性起控制作用，只需求解结构前几阶自振频率和振型即可满足工程要求［3-4］。根据算例的结构特点，本文采用子空间迭代法求解方程（1），得到算例的前六阶自振频率及振型如图2所示，主要包括面外振型（1阶）、面内振型（2、4阶）以及面内外耦合振型（3、5、6阶）三类振型。

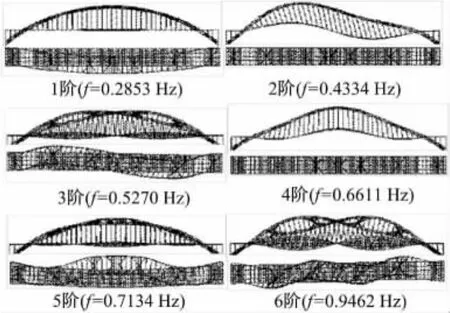
图2 自振频率及振型Fig.2 Fundamental frequencies and modes

算例的自振特性分析表明：①面外横向振动先于面内竖向振动出现，结构面外与面内基频之比为0.2853／0.4334＝0.7，体现了大跨钢管混凝土拱桥面外横向刚度弱的特点；②面外对称振型早于反对称振型出现，振动特性与梁相近；面外横向振型中，拱肋与桥面异步振动早于二者同步振型，说明桥面刚度对结构面外刚度有一定贡献；③面内振动首先出现面内反对称振型，体现了拱结构的振动特性；吊杆与立柱于结构面内有效传力，结构面内整体性更好，因此面内振型均为拱肋与桥面同步。

2.2 弹性稳定性分析

与结构无阻尼自由振动所体现的自振特性分析不同，弹性稳定性分析考虑了可能使结构刚度降低的外荷载作用，将几何刚度矩阵引入结构动力平衡方程，由振动频率为0时结构屈曲这一条件再次将问题转化为如下特征值求解问题：

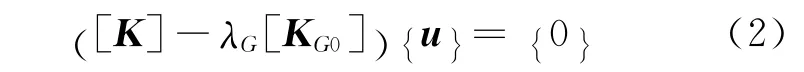
式中：［KG0］为基准荷载对应的几何刚度矩阵；λG为荷载因子或屈曲系数［14］。

求解特征方程（2），得到结构第i阶屈曲系数λi及相应屈曲模态向量｛u｝i。其中，一阶屈曲系数即为结构的弹性稳定系数，相应的振型向量为结构屈曲模态［11］。

依据现行《公路桥涵设计通用规范》（JTG D60－2004），算例计算荷载工况主要考虑了恒载、汽车荷载（公路－Ⅰ级）、人群荷载和风荷载。车道荷载表现为均布荷载加集中荷载的形式，双向六车道取车道折减系数为0.55，纵向折减系数为0.97；人群活载3.5kPa，横向布置于2m宽人行道内，不进行车道折减；风荷载施加于迎风面拱肋节点。综上，计算荷载工况见表2。

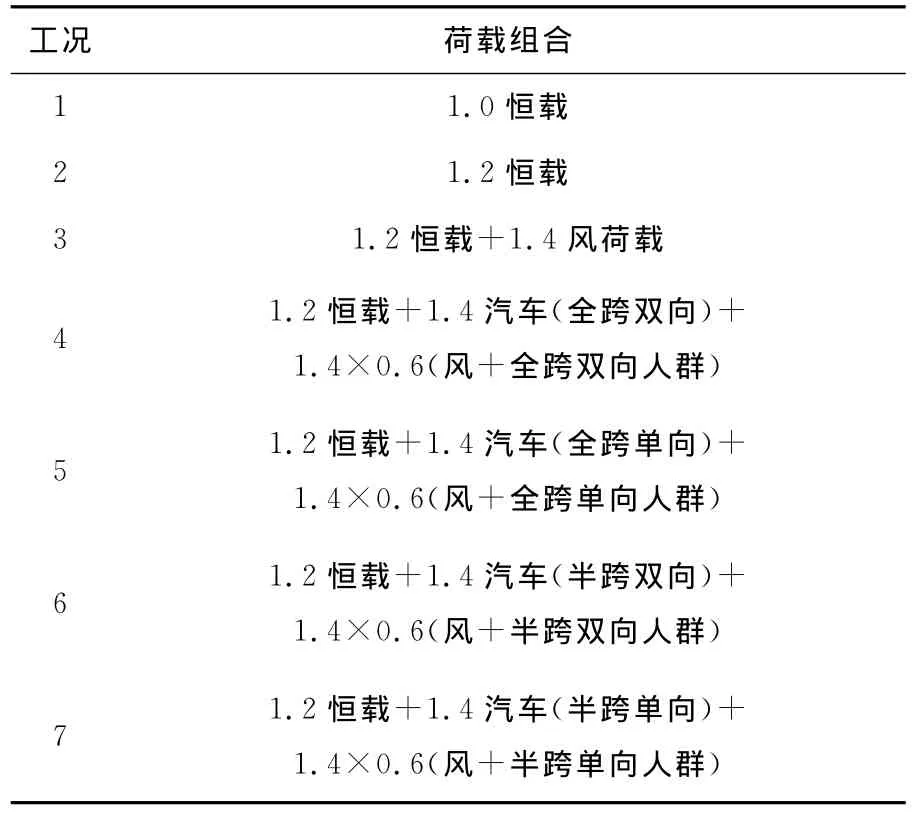
表2 荷载工况Table 2 Load cases

图3为弹性稳定系数－荷载工况散点图，由于荷载分项系数取值的不同，工况1对应的弹性稳定系数明显高于其余工况；其余工况尽管活载布载形式不同，但弹性稳定系数非常接近。主要是因为大跨桥梁的恒载比重较大，对桥梁静力性能起控制作用。在荷载工况作用下，算例均发生拱肋面外横向反对称屈曲，可见大跨钢管混凝土拱桥面外刚度较弱。

2.3 非线性稳定性分析

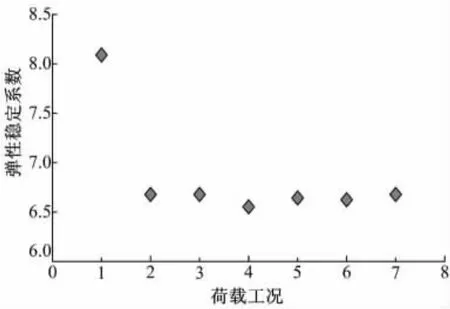
图3 弹性稳定系数－荷载工况散点图Fig.3 Scatter points between elastic stability coefficient and load case

依据文献［10］的分析结果，本文在对算例进行双重非线性稳定性分析时，以设计荷载为基准荷载，考虑桥面系的非保向力作用，等比例加载至结构发生横向失稳破坏，将此时结构基准荷载的倍数记为弹塑性稳定系数，以λcr表示。

由结构稳定系数－荷载工况关系曲线（见图4）可知，恒载对算例的稳定系数起决定性作用；弹性稳定系数与弹塑性稳定系数变化趋势相近，前者约为后者的2.70倍，说明非线性因素对算例稳定系数的取值影响较大，但对其变化规律影响甚微。

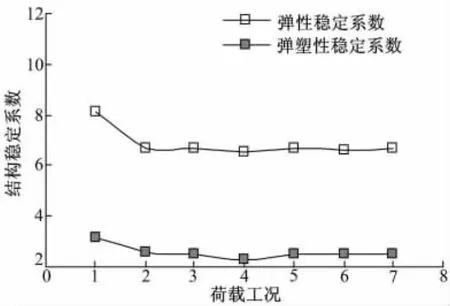
图4 稳定系数－荷载工况关系曲线Fig.4 Relationship curves of stability coefficient－load cases

3 矢跨比的影响

3.1 矢跨比对自振特性的影响

算例矢跨比由1／2降至1／10，进行自振特性分析。分析结果显示，面内振型随矢跨比的降低呈现提前的趋势；矢跨比为1／2时，虽然结构面内外基频之比有所增加（见图5），但此时结构高度大、刚度小，基频较低；随矢跨比的降低，拱肋与桥面系距离减小，吊杆、立柱等传力构件的线刚度随之提高，对拱肋的约束作用加强，体现为面内外基频平缓加大（见图5）；但降低矢跨比在提高拱肋横向侧倾约束的同时，结构面内整体性也在加大，因此基频之比变化不大，基本在0.7左右浮动。

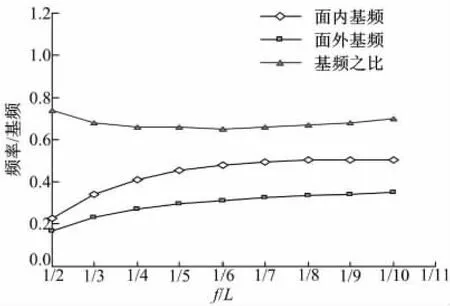
图5 频率／基频之比－矢跨比关系曲线Fig.5 Natural frequencies－rise－to－span relationship curves

3.2 矢跨比对稳定性的影响

算例矢跨比自1／2降至1／10，由弹性稳定性分析得到表2中各荷载工况对应的结构弹性稳定系数λ－矢跨比f／L关系曲线如图6所示，再次体现了恒载对稳定性变化趋势的控制作用，同时考虑到工况3作用下拱肋横向刚度最弱［10］，本文后续分析均以工况3加载。

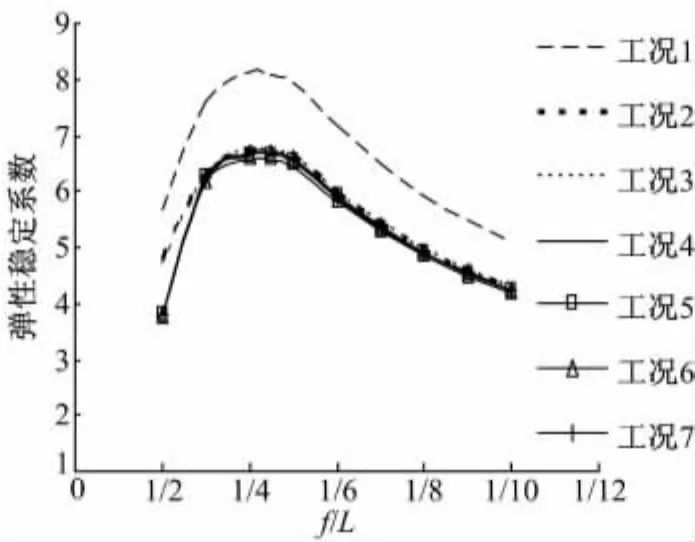
图6 弹性稳定系数－矢跨比关系曲线Fig.6 Relationship curves of elastic stability coefficient and rise-to-span ratio

以工况3为基准荷载，对算例进行双重非线性稳定分析，得到稳定系数－矢跨比归一化曲线如图7所示。可见，弹性稳定系数与弹塑性稳定系数变化趋势相近；与自振频率的单调增加不同，稳定系数随矢跨比的降低呈现先增大再减小的变化趋势，矢跨比f／L在1／4附近取值时，结构稳定系数较大。

综上，矢跨比对结构自振特性和稳定性的影响有所不同，仅靠自振特性的分析结果评价矢跨比的取值不全面。另外，拱圈材料用量随矢跨比的降低而降低，矢跨比不超过1／4时，由于矢跨比不同造成的拱圈材料用量的差异小于10%［10］。因此，本文算例的矢跨比宜在1／4附近取值。

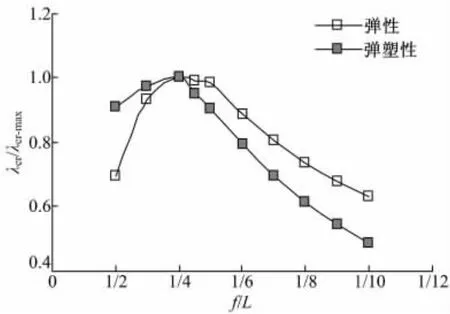
图7 稳定系数－矢跨比归一化曲线Fig.7 Stability coefficient vs.rise-to-span unitary

4 拱面内倾角的影响

以拱面与桥面的交线为轴，将算例的平行拱面向内转动一定角度得到提篮拱，并进行自振特性及工况3作用下的稳定性分析。

4.1 拱面内倾角对自振特性的影响

随拱面内倾角θ的增大，算例前10阶振型中面内振型的数量提高，面外振型的出现越来越晚、其阶次逐渐变大；θ的变化主要对结构面外一阶振动及反对称型耦合振动频率影响较大，对面内振动及对称型耦合振动频率影响很小。

以拱面平行（θ＝0°）时的基频为基准，面外基频随θ的增大显著提高，θ＝18°时提高幅度为57.3%；面内基频则略有降低，θ＝18°时约降低2%。可见，在本文讨论的参数取值范围内，随内倾角的增加结构面外刚度明显改善，面内刚度变化甚微。

4.2 拱面内倾角对稳定性的影响

不同拱面内倾角对应的稳定系数计算结果见表3，可见由于几何及材料非线性因素的影响，弹塑性稳定系数明显低于弹性稳定系数。

随θ的增加，算例弹性及弹塑性稳定系数均有所增加，前者提高幅度可达5.0%（θ＝4°时），后者最大可提高约1.6%（θ＝6°时）；当内倾角超过10～12°后，稳定系数反而有所降低，说明拱肋内倾后，拱顶附近横撑刚度提高、结构宽跨比增大、重心降低均对提高横向面外刚度有利；但内倾会使拱肋在受压的同时产生附加扭矩，又对承载不利。

内倾角的变化对弹塑性稳定系数的影响不如对弹性稳定系数的影响明显，主要是因为考虑材料非线性后，拱肋中存在的内力重分布使得结构极限承载能力变化不大，但随内倾角的增加拱顶最大横向位移显著降低，体现了拱肋内倾使结构横向刚度提高。

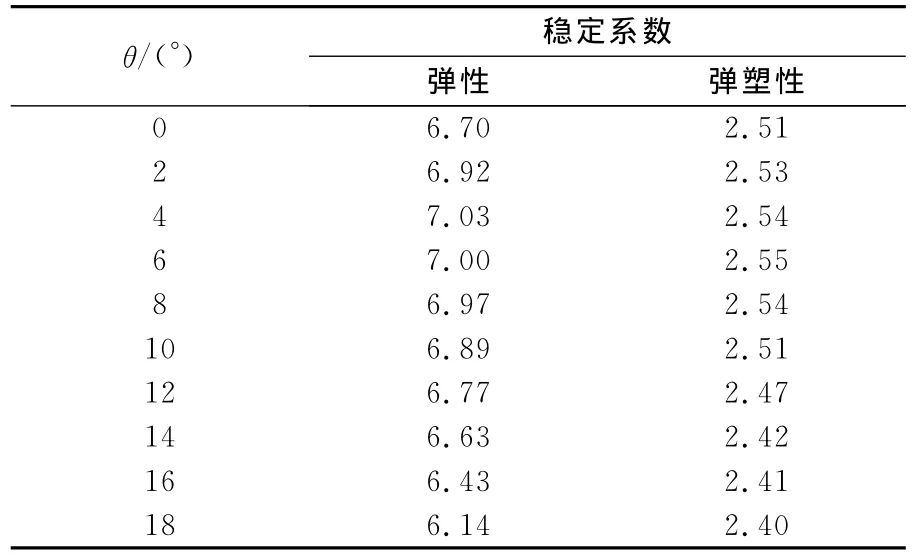
表3 内倾拱稳定系数Table 3 Stability coefficients of arch bridges with inclined ribs

5 结 论

（1）降低矢跨比对改善结构自振特性有利，矢跨比越接近1／4，结构稳定系数越高。实际设计时宜综合自振特性、稳定性的分析结果，并考虑拱圈材料用量决定矢跨比的取值。

（2）拱面内倾可有效改善结构面外刚度，表现为随拱面内倾角的加大面外基频提高，设计荷载作用下拱肋横向位移降低，但内倾过大会产生较大的附加扭矩，结构极限承载能力反而会有所降低。本文算例内倾角越趋近于4°稳定系数越高，内倾角超过10°稳定系数反而较拱肋平行时有所降低。

（3）由于非线性因素的影响，大跨径钢管混凝土拱桥弹塑性稳定系数显著低于其弹性稳定系数，但二者的变化趋势相近，弹性稳定系数能在一定程度上反映结构参数对稳定性的影响。因此，可在初步设计阶段综合自振特性与弹性稳定分析的结果确定结构参数的取值，以达到既能考虑荷载作用对稳定性的影响又能快速合理确定参数取值的目的。

［1］陈宝春，刘福忠，韦建刚.327座钢管混凝土拱桥的统计分析［J］.中外公路，2011，31（3）：96－103.Chen Bao－chun，Liu Fu－zhong，Wei Jian－gang.Statistical analysis on 327CFST arch bridges［J］.Journal of China and Foreign Highway，2011，31（3）：96－103.

［2］王頠，马青松.结构参数对下承式钢管混凝土拱桥动力特性的影响［J］.桥梁建设，2011（2）：34－38.Wang Wei，Ma Qing－song.Influences of structural parameters on dynamic characteristics of throughtype CFST arch bridges［J］.Bridge Construction，2011（2）：34－38.

［3］孙昊，钱永久，蔡迎春.结构参数变化对钢管混凝土拱桥动力特性的影响分析［J］.重庆交通大学学报：自然科学版，2009，28（6）：982－985，1074.Sun Hao，Qian Yong－jiu，Cai Ying－chun.Influences of structural parameters on dynamic characteristics of CFST arch bridges［J］.Journal of Chongqing Jiaotong University （Natural Sciences），2009，28（6）：982－985，1074.

［4］刘沐宇，龚凯，孙向东，等.单肋斜撑钢管混凝土拱桥动力特性分析［J］.武汉理工大学学报：交通科学与工程版，2009，33（6）：1104－1107.Liu Mu－yu，Gong Kai，Sun Xiang－dong，et al.Dynamic characteristics analysis of a single rib CFST arch bridge［J］.Journal of Wuhan University of Science and Engineering（Transportation Sciences and Engineering），2009，33（6）：1104－1107.

［5］何伟，赵顺波，杨建中，等.大跨宽幅双提篮系杆拱桥动力特性和抗震性能［J］.振动、测试与诊断，2010，30（6）：630－633.He Wei，Zhao Shun－bo，Yang Jian－zhong，et al.Dynamic and aseismic behavior of large－span tied arch bridge［J］.Journal of Vibration Measurement and Diagnosis，2010，30（6）：630－633.

［6］谭国宏，李龙安.某下承式钢管混凝土拱桥二类稳定分析研究［J］.桥梁建设，2011（3）：36－39.Tan Guo－hong，Li Long－an.Ultimate point instability analysis on a through－type CFST arch bridge［J］.Bridge Construction，2011（3）：36－39.

［7］郑永卫，包泮旺，沈旭东，等.舟山松岱大桥双重非线性稳定性分析［J］.公路，2011（8）：52－55.Zheng Yong－wei，Bao Pan－wang，Shen Xu－dong，et al.Nonlinear stability analysis on Zhou Shan Songdai Bridge［J］.Highway，2011（8）：52－55.

［8］陈宝春，郑皆连.钢管混凝土拱桥实例集（一）［M］.北京：人民交通出版社，2002：145－181.

［9］钟善桐.钢管混凝土结构［M］.3版.北京：清华大学出版社，2003：34－52.

［10］云迪.大跨中承式钢管混凝土拱桥静力及抗震性能［D］.哈尔滨：哈尔滨工业大学土木工程学院，2007.Yun Di.Static and aseismic behavior of large span half－through CFST arch bridges［D］.Harbin：School of Civil Engineering，Harbin Institute of Technology，2007.

［11］陈宝春.钢管混凝土拱桥设计与施工［M］.北京：人民交通出版社，1999：132－167，182－192.

［12］杨永清.钢管混凝土拱桥横向稳定性研究［D］.成都：西南交通大学土木工程学院，1998.Yang Yong－qing.Lateral stability of CFST arch bridges［D］.Chengdu：School of Civil Engineering，Southwest Jiaotong University，1998.

［13］Clough Ray W，Penzien Joseph.Dynamics of Structures［M］.3rd ed.California：University of California Press，1995：201－210.

［14］张素梅，云迪.大跨中承式钢管混凝土拱桥的横撑布置［J］.吉林大学学报：工学版，2009，39（1）：108－112.Zhang Su－mei，Yun Di.Lateral brace arrangement for large－span half－through concrete filled steel tube arch bridge［J］.Journal of Jilin University（Engineering and Technology Edition），2009，39（1）：108－112.