基于薄壁梁耐撞性理论的乘用车前纵梁轻量化设计

张君媛，陈 光，武栎楠 刘 嬴

（吉林大学 汽车仿真与控制国家重点实验室，长春 130022）

前纵梁是乘用车车身结构重要的纵向受力薄壁梁构件，在整车正面全宽碰撞（FRB）中，50%～70%的力由前纵梁吸收和传递［1－2］。随着汽车正面抗撞性要求的提高，前纵梁的刚度逐渐增大，质量也相应增加［3］。

目前，前纵梁结构设计方法有试验法、有限元仿真分析和公式法。试验法和有限元法都是在结构的详细设计完成以后才能进行，无法实现结构的正向设计。公式法则应用薄壁梁耐撞性理论建立结构特性（截面尺寸和材料）与耐撞性（平均压溃反力和最大弯曲力矩）之间的联系。该方法可用于从性能到结构（即从无到有）的正向设计中。

本文利用薄壁梁结构与压溃反力和弯曲力矩之间的关系，选择满足前纵梁子结构抗撞性标准和轻量化目标的截面形式和厚度，实现了前纵梁结构的正向设计。

1 前纵梁抗撞性目标及其分解

本文以汽车车身B柱的减速度－时间曲线（即碰撞波形）作为整车正面抗撞性的评价指标。以某国产中级轿车为例，探讨了不改变正面抗撞特性的同时，通过正向设计纵梁截面形状和厚度，实现其结构轻量化的方法。

该车整车质量约为1.37t，其有限元模型已通过试验验证。在65km／h正面全宽刚性墙碰撞时，整车前端结构达到最大变形，因此，以该工况作为研究工况，如图1所示。

图1 整车工况Fig.1 Boundary of the whole vehicle

原车碰撞总能量为218kJ，纵梁在碰撞中共吸收了52.5kJ的能量，在前端压溃空间不变的情况下，纵梁在碰撞中产生的压溃反力和抗弯力矩的大小对整车正面抗撞性（碰撞波形）的影响很大。

将原车纵梁按照截面和位置的不同划分为5个子结构，如图2所示。Z1段材料与其他部位不同；Z2段后部纵梁截面在y轴方向的宽度变小；Z4段位于纵梁拐角部位；Z5与Z3段不在垂直平面内。

子结构Z1段为压溃变形；Z2段受Z3段前部弯曲的影响，变形不大，但是对Z1段的压溃起到支撑作用，因此，考察Z2段的压溃特性。如图3所示，Z3～Z5段在碰撞中均表现为弯曲变形，因此，应当考察Z3～Z5子结构在碰撞中的抗弯性能。

以平均压溃反力作为Z1段和Z2段的抗撞性评价指标。对Z1和Z2段进行单独加载，加载方式如图4所示。Z1和Z2段一端固定，刚性墙以65 km／h的速度撞击另一端，通过对刚性墙添加质量点的方式保证Z1和Z2段在碰撞中产生较为彻底的压溃变形。仿真分析得Z1和Z2段的平均压溃反力FZ1和FZ2分别为83kN和182kN。

图2 纵梁分段Fig.2 Segments of the rail

图3 Z3～Z5段变形方式Fig.3 Buckling of Z3～Z5substructures

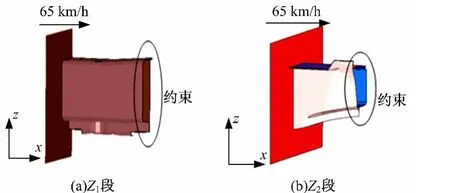
图4 Z1段和Z2段的压溃加载方式Fig.4 Crushing load on Z1and Z2

弯曲特性的评价通常为三点加载方式［4－5］，如图5所示。纵梁由一侧的两个固定刚体支撑，另一侧的刚体以4m／s的速度向纵梁运动使其产生弯曲变形。

采用该方法对Z3～Z5段纵梁进行加载，如图6所示，上侧的两个刚体支撑，下侧的刚体向上运动使每段纵梁产生90°弯曲角度。得到纵梁在弯曲时吸收的能量E，根据M＝E／θ，可得原车中纵梁子结构Z3～Z5的抗弯力矩。Z3～Z5段的平均弯曲力矩MZ3、MZ4和MZ5分别为4110、3320和2558N·m。

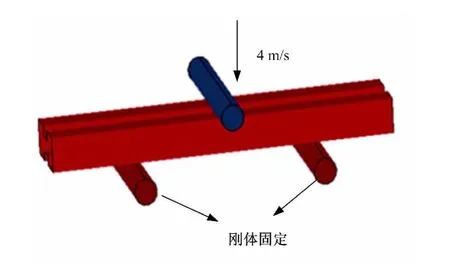
图5 结构的弯曲加载工况Fig.5 Bending load on the structures

图6 子结构Z3～Z5段加载工况Fig.6 Loading on Z3～Z5substructures

2 前纵梁压溃变形部分轻量化设计

2.1 多直角截面薄壁梁压溃反力表达式推导

文献［6］将矩形截面薄壁梁划分为4个中心角为直角的超折叠单元，作为压溃变形的基本组成部分，如图7所示。每个单元的塑性变形简化为3类:环形面拉伸、绕水平固定铰线弯曲和绕倾斜塑性铰线弯曲。各部分的能量耗散如式（1）～式（3）所示。

式中:当中心角φ为直角时，I1为0.53，I3为1.15；c为两翼长度之和，即e与f之和；H为折叠半波长；M0＝σ0h2／4为塑性极限弯矩，σ0为薄壁梁材料的等效流动应力，h为薄壁梁壁厚；b为环形面圆环子午线方向的半径。

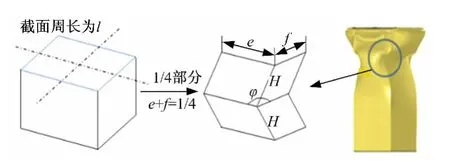
图7 超折叠单元Fig.7 Superfolding element

根据矩形截面的推导可以发现，由于环形面拉伸和倾斜铰线均出现在截面直角的拐角处，所以，当截面周长和厚度不变时，直角个数越多，则平均压溃反力越大。下面推导多直角截面的平均压溃反力表达式。

当某薄壁梁截面由n个直角组成时，薄壁梁在压溃时，会出现n个环形面拉伸和n个倾斜固定铰线。因此，当截面周长为l时，可分解为n个中心角为直角的超折叠单元，则有:

由能量最小原则，即:

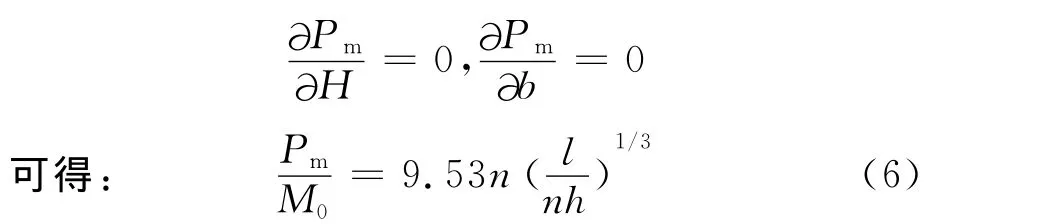
由于超折叠单元的有效压溃距离δe小于2 H［7］，如式（7）所示:

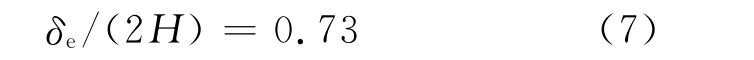
因此，得到n个直角截面的薄壁梁的平均压溃反力为

对于本文所涉及到的材料，当σ0取为材料的屈服应力时，式（8）的计算结果和薄壁梁压溃工况下的有限元仿真结果更为接近。

2.2 纵梁压溃变形部分截面设计方法

纵梁Z1段的抗撞性评价指标为其平均压溃反力83kN。将Z1段的轻量化目标设定相对原结构质量减轻20%。

原截面如图8所示，由两部分组成，材料屈服极限相同，均为441MPa。右半部分总长为308 mm，厚度为1.6mm，左半部分总长为182mm，厚度为1.4mm。将原截面周长490mm作为初始值，当质量减轻20%时，厚度应为1.2mm，计算得截面的直角个数n为12.5。由于n为13的结构不易实现，本文将n圆整为12，即选择如图9所示的十二直角截面作为Z1段截面的设计结果。根据结构的空间布置调整截面周长，保持新截面与原截面的长宽比相同，具体尺寸如图10所示，周长为463mm时，截面厚度为1.2～1.3mm。

图8 原Z1段截面组成Fig.8 Original cross section of Z1

图9 Z1、Z2段轻量化设计截面和结构图Fig.9 Cross section and structure of Z1and Z2

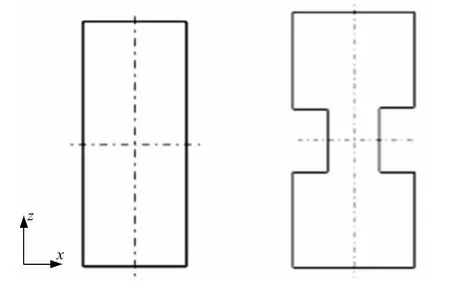
图10 矩形和十二直角薄壁梁截面Fig.10 Rectangle and 12right－angles cross section

由于Z2段和Z1段相连接，Z2段也采用如图10所示的结构形式。将Z2段子结构的平均压溃反力182kN和材料的屈服极限412.3MPa代入式（8）可以求得Z2段的厚度为2.0mm。由于空间限制，Z2段的截面是渐变的（见图2），因此Z2段的厚度取值范围为2.0～2.1mm。

3 前纵梁弯曲变形部分轻量化设计

3.1 十二直角截面薄壁梁压溃反力表达式推导

十二直角和矩形薄壁梁的截面如图10所示，周长均为404mm；长宽比为2.26（140／62）。采用图6所示的加载工况对两薄壁梁加载，使薄壁梁产生绕z轴的弯曲变形。

当厚度取值分别为1.6，1.8，2.0，2.2，2.4，2.6，2.8mm 时，在薄壁梁产生90°弯曲时所吸收的能量值对比如图11所示。十二直角截面的薄壁梁的吸能量大于矩形截面薄壁梁的吸能量。所以Z3和Z4段采用十二直角截面可以在保证原结构抗弯能力的基础上进行轻量化。为了保证Z5段和地板纵梁相连接，本文保持了其矩形截面，Z3～Z5段截面形式如图12所示。

图11 薄壁梁弯曲吸能量对比Fig.11 Energy dissipated by the bending of the thin－walled beams

图12 Z3～Z5纵梁形式Fig.12 Layout of rail Z3－Z5

3.2 纵梁弯曲变形部分截面设计方法

根据Kecman薄壁梁弯曲理论［8］，对于长为a，宽为b，厚度为h，材料的屈服强度为Y的矩形截面薄壁梁受到绕长边方向的弯曲破坏时，产生的最大弯矩为

根据文献［8］中大量的试验数据和本文的仿真分析，空矩形薄壁梁的平均弯矩约为最大弯矩的0.3～0.5倍。由于Z5段为矩形截面，将子目标分解得到的Z5段的平均弯曲力矩代入式（9）～（12），得到Z5段厚度约为2.4～2.5mm。

Z3段和Z4段的截面形状不属于矩形截面，用式（9）～式（12）不能对其厚度进行准确估计。Z3段最大弯矩不小于 MZ3，由式（9）～式（12）预估Z3段厚度为2.3mm，再在如图5所示的Z3段弯曲工况下采用有限元分析对Z3段厚度进行修正，Z3段厚度应为2.4～2.5mm。采用同样的方式得Z4段厚度应为2.0～2.1mm。所设计的新纵梁如图13所示。各段材料性能和厚度列于表1中。

图13 新纵梁结构Fig.13 Structure of the new rail

表1 新纵梁子结构材料性能和厚度Table 1 Performance and thickness of the substructures material of the new rail

4 整车集成和抗撞性验证

新设计的纵梁子结构Z1～Z5各段厚度值都取为下限和上限，并将这两个纵梁集成于整车之中，如图14所示，进行两次整车正面全宽刚性墙碰撞（车速为65km／h）有限元分析。纵梁结构的吸能量与原车的对比结果如表2所示，图15为采用新设计的纵梁后，加速度波形与原车的加速度波形的比较。

图14 纵梁在前端的位置Fig.14 Location of the new rails in the front of the car

表2 改进前、后纵梁吸能量对比Table 2 Energy dissipated by the original and developed rails

图15 纵梁设计前、后整车加速度波形比较Fig.15 Acceleration pulses of the whole vehicle with the original and new rails

根据表2和图15对比，虽然纵梁各子结构厚度取为下限时，波形的第一个峰值更为接近，但是取为上限时，总吸能量和B柱下部加速度波形整体都比较接近。因此，本文将各纵梁子结构厚度上限作为纵梁轻量化的最后结果。此时，新纵梁质量为11.96kg相对原纵梁质量14.93kg减轻了约3kg，即20%。

本文在理论上提出了一种以薄壁梁力学理论为基础，以轻量化和抗撞性为性能目标的截面优化方法。在工程实际中，纵梁的封闭截面是由两块钢板焊接而成。根据文中薄壁梁压溃理论，当保证截面周长和截面的形式不变时，薄壁梁的平均压溃反力相差不大，因此可将十二直角形式的纵梁截面修改成为由两块钢板分别成型后焊接到一起的形式，如图16所示，在保证截面周长不变的基础上，具体尺寸可根据焊接需要调整。每段子结构的连接和厚度变化可以根据实际情况通过激光拼焊或焊接加强板的方式来实现。通过实际的工艺设计，结构的轻量化效果可能小于20%，这时可以根据实际情况在轻量化目标设计时采用一个修正系数，即可得到解决。工艺和目标系数的确定是本文需要进一步研究的内容。

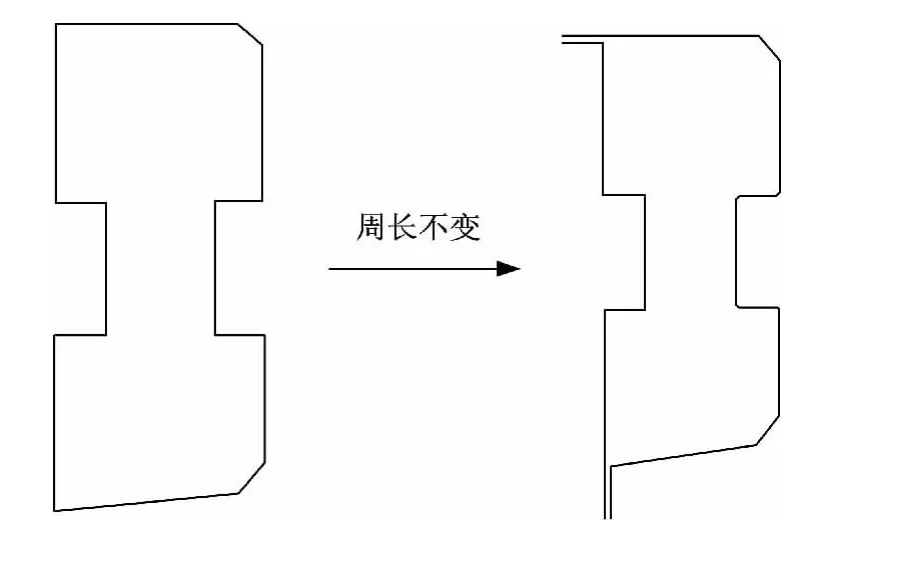
图16 截面工程修改示意图Fig.16 Schematic diagram of engineering modification on the cross section

5 结 论

（1）按照纵梁不同部位的变形和吸能情况进行目标分解，压溃变形为主的部位以平均压溃反力作为该部位的抗撞性评价标准；弯曲变形为主的部位以弯曲变形的平均弯曲力矩（或吸能量）作为抗撞性评价标准。这种目标分解方法可用于结构设计中。

（2）采用多个直角薄壁压溃反力表达式，得到了十二直角截面的纵梁截面形式。根据连接和弯曲变形的需要对结构厚度进行调节。在保证整车正面抗撞性的基础上，纵梁质量减轻了约20%，达到了不改变安全性的轻量化设计的目的。

［1］张君媛，陈光，刘乐丹，等.乘用车结构正面抗撞性波形设计与目标分解［J］.吉林大学学报:工学版，2012，42（4）:823－827.Zhang Jun－yuan，Chen Guang，Liu Le－dan，et al.Design and target cascading of objective pulse of car frontal crashworthiness［J］.Journal of Jilin University（Engineering and Technology Edition），2012，42（4）:823－827.

［2］Malen D E.Fundamentals of Automobile Body Structure Design［M］.Pennsylvania USA:SAE International，2011:224－226.

［3］Zarei H R，Kröger M.Bending behavior of empty and foam－filled beams:Structural optimization［J］.International Journal of Impact Engneering，2008，35（6）:521－529.

［4］Park C，Kan C，Reagan S，et al.Crashworthiness and numerical analysis of composite inserts in vehicle structure［C］∥SAE Paper，2012－01－0049.

［5］Abramowicz W，Jones N.Dynamic axial crushing of square tubes［J］.International Journal of Impact Engineering，1984，2（2）:179－208.

［6］Abramowicz W，Jones N.Dynamic progressive buckling of circular and square tubes［J］.International Journal of Impact Engineering，1986，4（4）:243－270.

［7］Kecman D.Bending collapse of rectangular and square section tubes［J］.International Journal of Mechanical Sciences，1983，25（9－10）:623－636.

［8］唐洪斌.乘用车正面抗撞性设计方法研究［D］.长春:吉林大学汽车工程学院，2008.Tang Hong－bin.Study on design procedures of frontal crash worthiness for passenger car［D］.Chanchun:The College of Automotive Engineering，Jilin University，2008.