用于地铁车辆的不锈钢型材拉弯成形缺陷

王胜满

（1.大连交通大学 材料科学与工程学院，辽宁 大连 116028；2.长春轨道客车股份有限公司，长春 130061）

不锈钢车体具有重量轻、安全性好、抗腐蚀性能强、使用寿命高等突出优点，已大量应用于地铁、轻轨等城市轨道车辆的生产制造［1］。

不锈钢车体制造的关键技术之一是结构件的拉弯成形技术。车顶弯梁、端弯梁等多种车顶构件都是用不锈钢型材采取拉弯工艺成形的。但拉弯工艺技术难度大，影响因素多［2－4］，而不锈钢又是一种难变形材料，致使拉弯件的成形精度很难控制，成形件极易出现起皱、截面畸变及轮廓精度差等诸多缺陷，严重影响了产品的质量［5－7］。

本文以某地铁车辆不锈钢车体的车顶弯梁为典型件，采用数值模拟软件对构件的拉弯成形工艺进行了模拟研究，对预拉、弯曲拉伸、补拉等主要工艺参数进行了模拟优化，分析研究了主要成形缺陷的成因和控制方法，并加以试验验证。

1 车顶弯梁拉弯成形模拟及缺陷

车顶弯梁材料为SUS301L－ST不锈钢，其截面及外形尺寸如图1所示。该构件外形尺寸大、弯曲半径变化大，壁厚小（1.5mm）、截面立边高（65mm），这种结构特点导致构件成形难度很大，成形中会出现多种缺陷，产品质量精度很难控制。

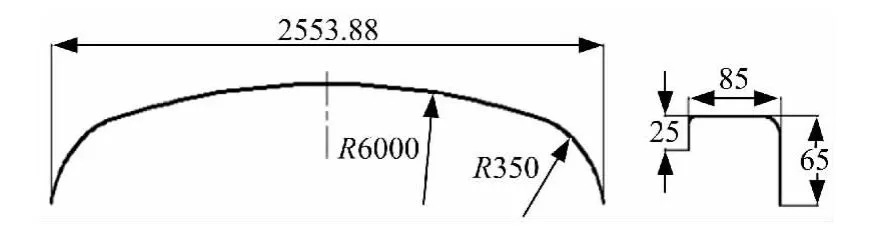
图1 车顶弯梁截面形状及轮廓尺寸Fig.1 Section shape and profile dimensions of roof carline

1.1 有限元模型的建立

1.1.1 材料模型

根据SUS301L－ST的单向拉伸试验测得材料的厚向异性指数r＝1.086＞1，故采用 Hill48正交各向异性屈服准则:

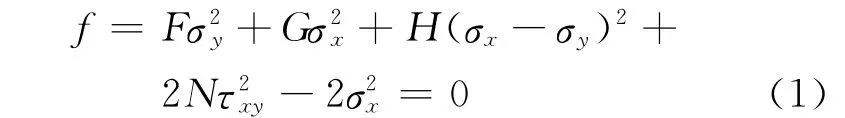
式中:f为屈服函数；σx、σy为应力分量；F、G、H、N为与材料各向异性参数有关的系数，表达式为:

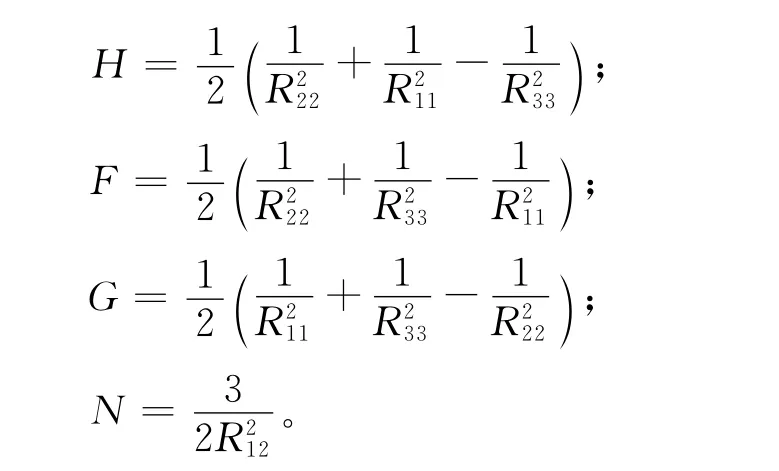
式中:R11＝1；

本文模拟采用等向强化的材料模型；使用Krupkowsky准则描述材料的真实应力－塑性应变行为

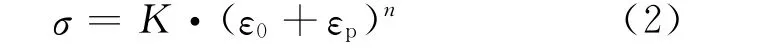
式中:σ为真实应力；ε0为初始塑性应变；εp为塑性应变；K＝1501.971MPa；n＝0.3365；ε0＝＝0.0428。

1.1.2 有限元建模

有限元模型如图2所示，由于结构对称，为了提高计算效率，取一半进行分析。采用S4R壳单元对型材进行离散化处理，厚向设置5个高斯积分点。约束拉弯胎、挡板和夹钳为刚体，与型材的罚接触因子μ＝0.1。夹钳与型材端面绑定，由夹钳带动型材包绕拉弯胎完成拉弯过程。由于加载轨迹长，材料在单方向上尺度大，夹钳网格节点的各坐标分量不在同一个数量级上，为防止夹钳刚体变形，将其简化为平面。

图2 拉弯有限元模型Fig.2 Finite element model of stretch bending simulation

1.2 模拟结果及缺陷分析

车顶弯梁拉弯成形的位移分布模拟结果如图3所示，可以看出:成形后构件主要有立边起皱、截面畸变（截面小立边外翻畸变）以及轮廓精度误差大等缺陷。

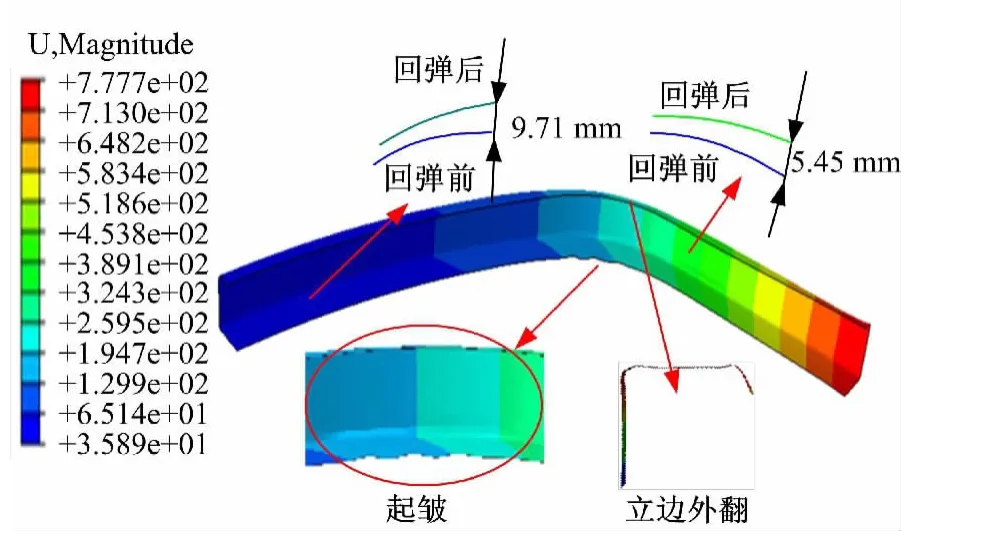
图3 位移分布模拟结果Fig.3 Simulation result of displacement distribution

（1）立边起皱。模拟结果表明:在构件半径为350mm的小弧段区域，高度为65mm的立边出现了明显的起皱现象。这是因为构件的壁厚小，截面立边高度大，弯曲半径小，弯曲变形大，而拉弯成形的拉伸量不足，立边底部很容易因弯曲受压而发生失稳起皱。

（2）截面畸变。从图3中的模拟结果可以看出:在构件的小弧段区域，高度为25mm的小立边出现了明显的外翻畸变。拉弯过程中随着拉伸量的不断增大，型材被拉长，截面收缩，宽度减小，小于胎具宽度，因而发生小边外翻缺陷。

（3）轮廓精度差。模拟结果表明:构件在大弧段中部轮廓精度误差最大达到9.71mm，小弧段轮廓精度误差为5.45mm，轮廓精度很差，无法满足使用要求。轮廓精度误差大主要是回弹引起的。不锈钢本身就是一种高强度难变形材料，弯曲后构件会出现很大的形状弹复；构件的拉弯胎具型面设计不准确，对回弹的补偿修正不准确；拉弯工艺参数不合理，型材弯曲时拉伸不足，塑性变形比例小，回弹大，也降低了构件的轮廓精度。

2 缺陷控制模拟及参数优化

2.1 立边起皱缺陷的控制

拉弯工艺参数影响拉弯件的拉伸变形量，通过改变工艺参数来改变拉伸变形量，能够减小甚至消除起皱现象。图4对预拉参数（Pre）、弯曲拉伸参数（Wra）、补拉参数（Pos）等拉弯工艺控制参数对拉伸变形量的影响进行了模拟分析。结果表明:Pre和Pos对拉伸变形量的影响不大，增加Pre、Pos只能在一定范围内改变拉伸变形量，而Wra对起皱现象影响很大，随着Wra的增加，拉伸变形量明显增大。但是随着拉伸变形量的增大，型材的延伸率增加，壁厚会减薄，将削弱构件的强度，截面畸变也更加严重，过大的拉伸量甚至会导致型材断裂。因此必须对拉伸量进行优化，确定既能消除起皱缺陷又能确保产品质量和截面精度的最佳的拉伸参数。图5为工艺参数优化后拉弯成形的模拟结果，可见起皱缺陷已经消失。

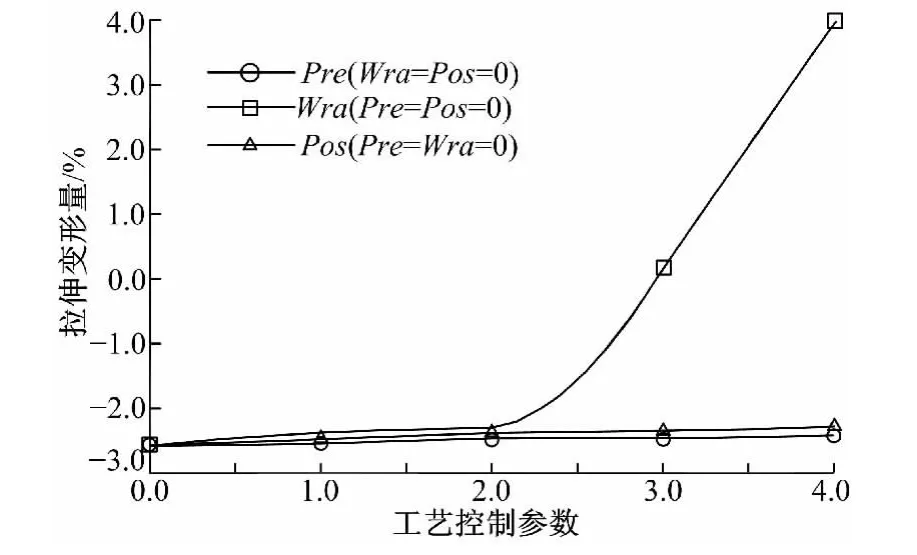
图4 工艺参数对拉伸变形量影响的模拟结果Fig.4 Influence of process parameters on stretch elongation by simulation

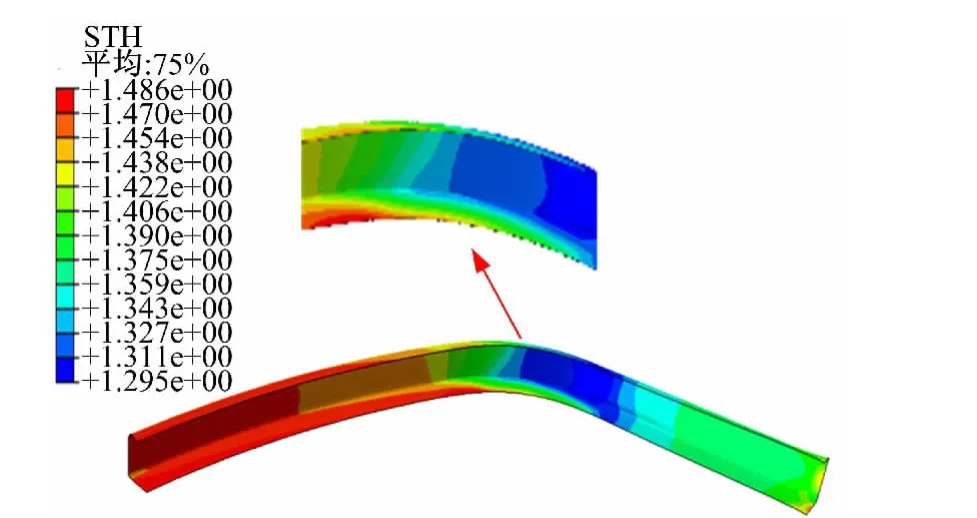
图5 工艺参数优化后的拉弯成形模拟结果Fig.5 Simulation results of stretch bending forming by optimized process parameters

2.2 截面畸变缺陷的控制

为了消除构件截面的小边外翻畸变的缺陷，对截面收缩量进行了模拟计算，根据计算结果对截面尺寸进行收缩补偿，以确保拉弯后拉弯件截面小边不与胎具发生干涉变形。图6为收缩量的预测结果，最大收缩量为11.41mm，因此型材截面宽度应该由原来的85mm增加到96.41mm。运用补偿后的型材截面数据进行拉弯成形模拟，结果如图7所示，可见，截面形状规则平整，小边外翻畸变消失。

图6 截面宽度收缩量模拟结果Fig.6 Simulation result of profile′s cross section shrinkage

2.3 轮廓精度缺陷的控制

拉弯件轮廓精度差主要是弯曲回弹引起的。Pre、Wra和Pos等拉弯控制参数是影响弯曲回弹量的主要因素，这些参数通过改变拉伸位移和弯曲角度来控制变形量，进而影响回弹量和轮廓精度。分别对Pre、Wra、Pos对车顶弯梁拉弯件轮廓精度的影响进行模拟分析，结果如图8所示。可以看出:增大Pre、Wra和Pos等工艺参数，可以减小成形件轮廓精度误差，其中弯曲拉伸量对轮廓精度影响最大，增大弯曲拉伸量能够明显减小轮廓误差，预拉量、补拉量也能在一定程度上减小轮廓误差。因此需要对拉弯工艺参数进行模拟优化，确定最佳工艺参数。同时，应根据回弹量模拟预测结果，对拉弯胎具的型面进行精准的补偿修正，以获得准确的拉弯胎具，减小拉弯件的轮廓误差，提高成形精度。

图7 截面收缩补偿后拉弯成形模拟结果Fig.7 Simulation results of stretch bending forming after the cross－section shrinkage compensated

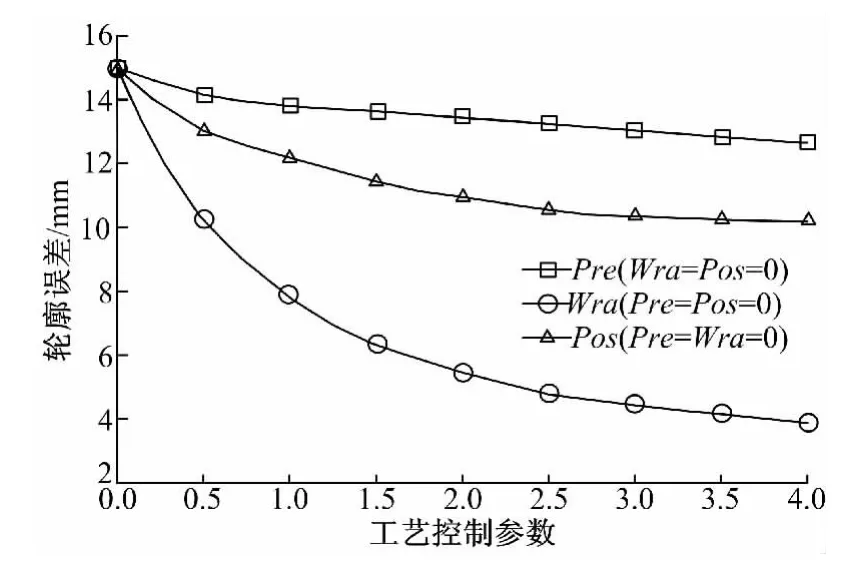
图8 工艺参数对轮廓精度影响的模拟结果Fig.8 Influence of process parameters on profile precision

3 成形试验

运用上述模拟结果，确定了车顶弯梁拉弯成形工艺参数，设计制造了补偿修正后的拉弯胎具，在美国Cyril Bath公司进口的V－75数控拉弯机上进行了成形试验，结果如图9所示。结果表明:成形件完全消除了起皱缺陷，而且截面各边平整，没有了畸变现象，最大轮廓精度误差仅有0.4 mm，精度指标完全达到设计要求，实现了高精度成形，也验证了本文研究成果的正确性和有效性。

图9 试验件和原构件精度对比Fig.9 Precision comparison between test part and original part

4 结 论

（1）弯曲拉伸量是影响不锈钢型材拉弯件的起皱缺陷的主要工艺参数，增加弯曲拉伸量能够有效控制起皱缺陷。

（2）车顶弯梁的小边外翻畸变缺陷是型材截面收缩引起的，对截面宽度收缩量补偿后，可以消除截面小边外翻的畸变缺陷。

（3）预拉量、补拉量等工艺参数对回弹影响较小，增加预拉量、补拉量能在一定程度上减小轮廓误差；弯曲拉伸量是影响回弹的重要参数，增大弯曲拉伸量能够明显减小回弹，提高轮廓精度。

［1］薛克仲.城市轨道车辆车体材料选择［J］.城市轨道交通研究，2003，6（1）:14－19.Xue Ke－zhong.Selection of car body materials for urban railway vehicles［J］.Urban Mass Transit，2003，6（1）:14－19.

［2］谷诤巍，刘化民，刘玉梅，等.不锈钢型材拉弯成形工艺模拟研究［J］.模具工业，2006，32（8）:42－44.Gu Zheng－wei，Liu Hua－min，Liu Yu－mei，et al.Simulation of stretch bending forming process of stainless section steel［J］.Die ＆ Mould Industry，2006，32（8）:42－44.

［3］刁可山，周贤宾，金朝海，等.复杂截面型材力控制拉弯成形数值模拟分析［J］.材料科学与工艺，2004，12（4）:413－416.Diao Ke－shan，Zhou Xian－bin，Jin Chao－hai，et al.A numerical study on the force－contr－olled stretch bending of aluminum extrusion with complex cross section［J］.Materials Science and Technology，2004，12（4）:413－416.

［4］Paulsen F，Welo T.Application of numerical simulation in the bending of aluminium－alloy profiles［J］.Materials Processing Technology，1996，58（2）:274－285.

［5］Clausen A H，Hopperstad O S，Langseth M.Sensitivity of model parameters in stretch bending of alu－minium extrusions［J］.International Journal of Mechanical Sciences，2001，43（2）:427－453.

［6］刁可山，周贤宾，李晓星，等.矩形截面型材拉弯成形［J］.北京航空航天大学学报，2005，31（2）:134－137.Diao Ke－shan，Zhou Xian－bin，Li Xiao－xing，et al.Stretch bending of aluminum extrusion［J］.Journal of Beijing University of Aeronautics and Astronautics，2005，31（2）:134－137.

［7］Hopperstad O S，Berstad T，Ilstad H，et al.Effects of the yield criterion on local deformations in numerical simulation of profile forming［J］.Journal of Materials Processing Technology，1998，80－81（1）:551－555.