基于多项式的等高齿锥齿轮时变啮合刚度建模

刘志峰，张志民，张敬莹，罗 兵

（北京工业大学 机械工程与应用电子技术学院，北京 100124）

0 引 言

关于对齿轮动力学系统及啮合刚度的研究，国外主要集中在时变啮合刚度计算方法的分析上，具有代表性的有 Song He［1］和 Robert G.Parker［2］，他们利用有限元方法计算并获得了齿轮时变啮合刚度。还有研究者曾尝试利用有限元方法建立齿轮时变啮合刚度的经验公式，或简化为与齿轮啮合频率同周期的方波函数，具有代表性的有Lin等［3］。国内此方面的研究者主要有唐进元、李润方、林腾蛟等［4－5］，时变刚度的计算方法也主要采用通用的有限元方法。韩勤锴等［6］提出一种简便实用的考虑轮齿延长啮合作用时的啮合刚度模型，称之为“梯形波模型”，给出了该模型主要参数（单齿和双齿啮合刚度、提前和滞后啮合时间）的确定方法。李亚鹏等［7］提出改进的石川公式，为齿轮动力学方程提供一个整体意义上的时变啮合刚度计算方法。刘国华等［8］提出了反向啮合刚度的概念，给出了渐开线直齿圆柱齿轮系统反向啮合刚度的求解过程，推导出在啮合区间变动及啮合点沿齿廓不断变动情况下轮齿啮合刚度的计算公式。在进行齿轮的动力学分析时，常见的方法是把刚度简化处理成多阶谐波叠加的形式，这种形式只是保证了刚度的变化频率。

本文针对航空航天机械传动中用的等高齿锥齿轮，提出采用多项式的形式对等高齿锥齿轮时变啮合刚度建模进行简化。并在不同的阻尼、载荷、转速工况下，将多项式函数展开的刚度模型和多阶谐波叠加形式的刚度模型进行分析对比。

1 等高齿锥齿轮时变啮合刚度原理

理论上，等高齿锥齿轮进行传动时，啮合的两个轮齿在每一瞬间只有一个点相互接触。由于轮齿表面的弹性变形，这些点沿轮齿齿面法线方向产生位移，于是轮齿之间形成一个椭圆接触区域，而不再是点接触的形式。如图1所示，齿面上连续的理论瞬时接触点的曲线形成一条接触轨迹。齿面上实际的接触区，就是由理论接触轨迹上的许多瞬时接触椭圆集合而成［9］。

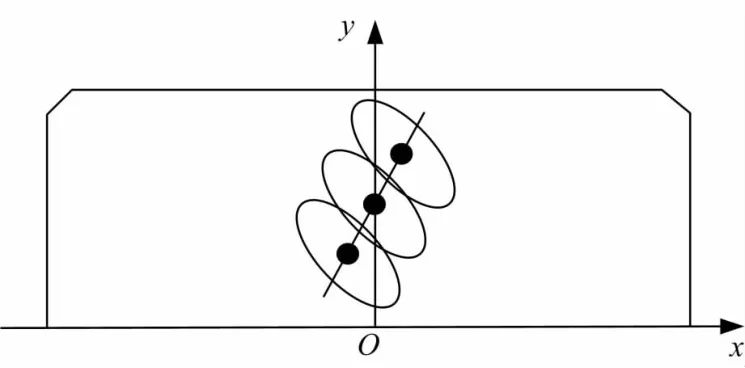
图1 实际接触区域Fig.1 Actual contact area

假设只有一对齿面工作。在啮合力作用下，轮齿发生两种形式的变形，即接触点沿齿面法向的位移和齿面上形成的椭圆接触区。在某一啮合点处，已知啮合点的法向位移p，根据齿轮的几何形状和该点的几何位置可以确定椭圆的具体尺寸。轮齿啮合刚度随着接触区域的变化而变化，接触区域越大，两个齿面啮合在一起的部分越多，越难以继续产生变形，即刚度值越大。当齿轮传递的载荷F较小时，接触点在齿面法线方向上产生很小的位移Δp，此时接触椭圆区域很小，啮合刚度K也较小；当传递的载荷很大时，形成的接触椭圆区域变大，啮合刚度K也随之变大。综上分析，可以认为刚度K值由椭圆接触区域的大小和形状决定，而椭圆接触区域又由接触点沿齿面法向的位移p决定。于是，假设单齿啮合刚度K是关于接触点沿齿面法向位移p的函数。

实际情况下，每一次啮合都有若干个理论接触点。这些接触点在各自的齿面上所处的位置不尽相同。它们大体上均匀分布在接触轨迹线上，有的靠近齿顶处，有的靠近齿根处，还有的靠近齿面中心。把实际中的若干接触点综合成一个虚拟的接触点，称之为综合啮合点。综合啮合点在齿面法线方向上的位移和在虚拟齿面上形成的接触椭圆形状分别由多个实际接触点的位移和齿面上椭圆形状综合而成。根据上文分析可知，综合啮合点的瞬时接触变形由轮齿的形状和多个实际接触点在各自接触轨迹线上的位置所决定。由于这多个接触点大体上均匀分布在接触轨迹线上，所以可以认为综合啮合点沿齿面法向的位移可以唯一确定一个接触椭圆，而与综合啮合点在齿面上的位置无关。因此，综合啮合刚度是一个关于综合啮合点的法向位移p的函数。

2 基于多项式时变啮合刚度的等高齿锥齿轮动力学方程

图2为等高齿锥齿轮扭转振动模型，该模型包含了时变啮合点、系统啮合刚度、啮合阻尼以及静态误差。非线性双自由度纯扭转振动系统简单描述了齿轮转动过程中齿对啮合的动力学特性，时变刚度引起动态稳定问题。该模型主要由两个圆盘与一个弹簧、一个阻尼器和一个静态误差组成。圆盘代表齿轮的惯性质量，弹簧代表齿轮啮合刚度，阻尼器代表轮齿的啮合阻尼。

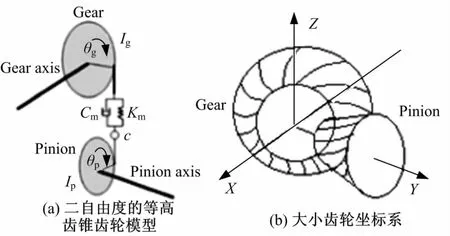
图2 等高齿锥齿轮扭转振动模型简化图Fig.2 Simplified figure of torsion and vibration of high－spiral bevel gear

双自由度动态模型（主动轮p，从动轮g）转动方程为

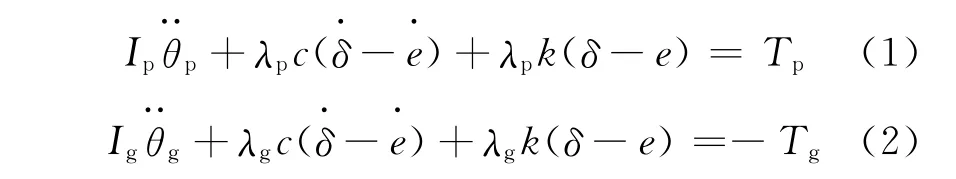
式中:e为静态传递误差；c为啮合阻尼；k为啮合刚度；λp和λg为啮合点半径；Ip和Ig为齿轮的转动惯量；θp和θg为齿轮转动角度；Tp和Tg为齿轮的转动力矩。

动态传递误差定义为

式中:cm为平均啮合阻尼；km为平均时变啮合刚度；动态误差p＝δ－e，e＝f′zzccos（ωt＋φ），f′zzc为齿轮等级精度影响齿轮副齿频周期误差的公差值。

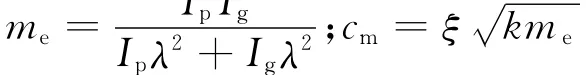
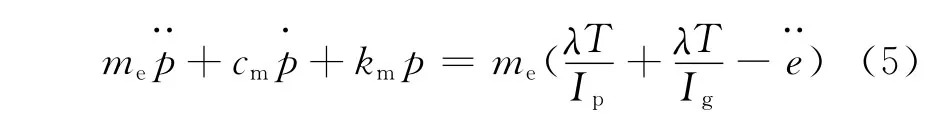
3 时变啮合刚度模型

啮合刚度分以下三种情况讨论。

3.1 平均啮合刚度值

齿厚b＝40mm，根据机械振动手册［10］齿轮传动中齿轮副的平均啮合刚度km与重合度ε＝1.6和轴向重合度εl＝0.6的函数关系图查得平均啮合刚度实测值，该实测值经过合理处理得

3.2 简谐波叠加形式的齿轮动力学数学模型

在进行齿轮动力学分析时，沿轮齿齿面法线方向的位移p是一个重要的待求量，其数值大小直接影响了齿轮的振动强度、疲劳及磨损。所以，在进行齿轮系统动力学分析时建立的振动方程常常是以p为未知量的一元二次微分方程。以文献［11］为例，最终化简得到的振动方程形式为

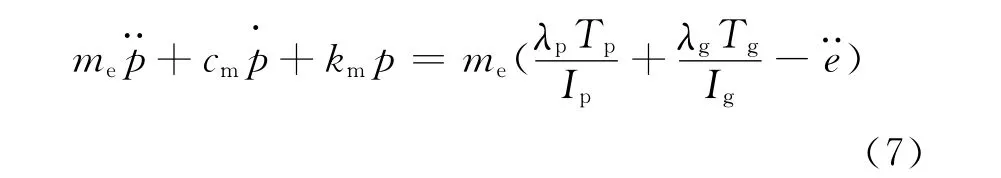
在分析方程时需要建立合理的刚度、阻尼、误差模型，在传统的文献中［12－14］，多数把它们表示为多阶简谐波叠加的形式。典型的刚度模型建立方法如下:

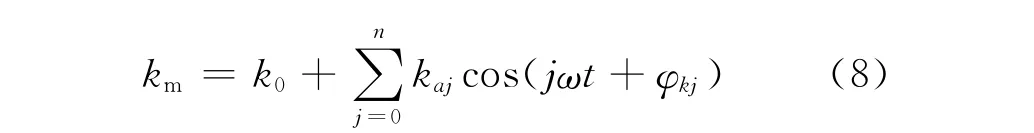
在求解时由于计算量的限制，往往只取第一阶简谐波。同理，建立起来的阻尼cm和静态传递误差e的模型具有类似的形式［12］。

式中:齿轮的啮合频率ω＝nπz／30，k0＝1，kaj＝0.2。

3.3 多项式时变啮合刚度模型

根据等高齿锥齿轮啮合刚度的变化规律，齿轮啮合刚度的大小与啮合区域的形状及位置有直接关系。在任一时刻，啮合区域中心点的位置和啮合面积的大小直接决定了啮合刚度。一对轮齿接触时，在啮合力的作用下，沿齿面法向的弹性位移p越大，啮合面积也就越大。因此，弹性位移p的值一定程度上对齿轮综合啮合刚度起决定作用。基于上文分析，假设啮合刚度k′m关于沿齿面法向位移p的函数关系具有多项式的形式:

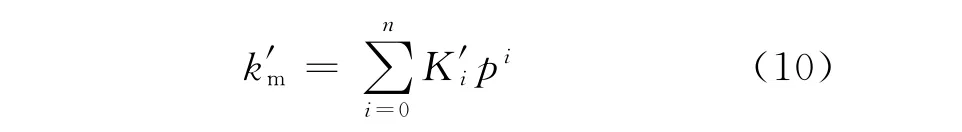
式中:K′i为刚度影响系数，i＝0，1，2，…。

得到的啮合刚度值中，只有前几项系数K′0，K′1，…，K′n，起较大作用，因此计算分析时只研究前几项即可:

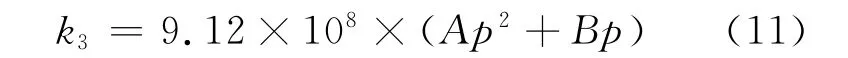
式中:A和B为多项式的系数，其数值为

A和B的数值是根据时变啮合刚度第一种情况:轮齿啮合刚度参考值计算得到的，计算依据是在某一段位移p中使刚度值在一定范围内，使得k2和k3可以进行比较，如图3所示。

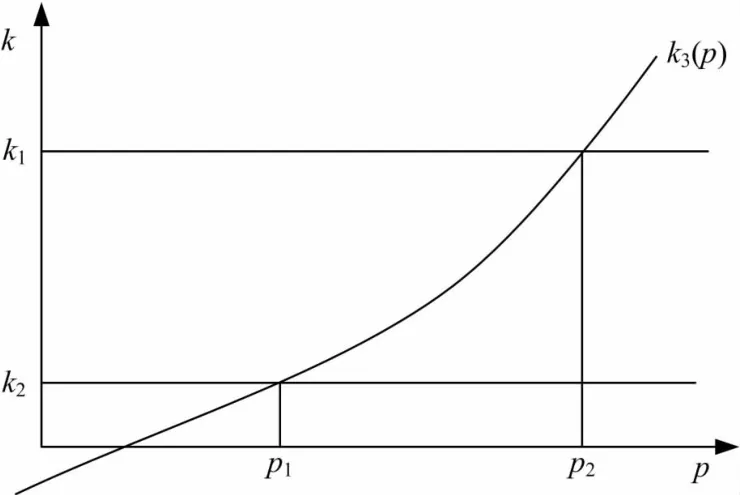
图3 刚度的范围Fig.3 Range of stiffness

如图4所示，将圆锥齿轮模型简化为圆锥台，C为啮合点，r代表啮合半径。主动轮的参数a＝20，b＝86，h＝35，r＝74；从动轮的参数a＝47，b＝86，h＝35，r＝74。转动惯量Ip＝1.0695×104、Ig＝8.6556×103，等效质量me＝0.8736 kg。

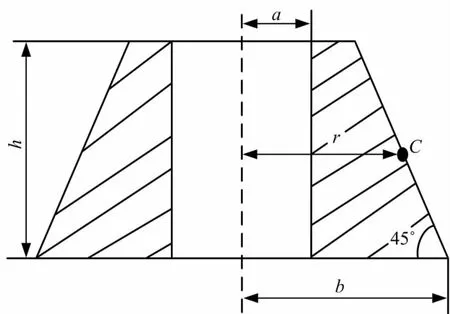
图4 摆线锥齿轮简化成的圆锥台模型Fig.4 Cone model of high－bevel gear

4 理论仿真分析

在未说明的情况下，所用到的相关数据为:齿轮等级为7级精度［15］，齿数z＝29，阻尼耗散因子系数cg＝0.05，振动频率ω＝nπz／30，K1代表时变啮合刚度参考值模型，K2代表多阶简谐波叠加形式的刚度模型，K3代表多项式形式的刚度模型。

4.1 K1、K2、K3 的时域响应计算比较

图5 K1、K2、K3 的时域响应图Fig.5 Time－domain response of K1，K2and K3

将刚度模型分别代入齿轮动力学方程中，用龙格库塔算法ode45函数计算，用计算结果得出时域响应图。其中由于刚度模型K1是常量，所以计算结果只取最终恒定值做时域响应分析。图5中红色线代表K1，绿色线代表K2，蓝色线代表K3，K3与K1图形变化趋势相同，K2呈余弦形式振动，K3和K1振动程度随着时间变化趋于稳定，并都趋于一条平衡线，齿轮随着转速n的增加而引起的振动更加剧烈，随着负载扭矩T的增加，这种振动程度减弱，表1为在不同转速、负载扭矩下最大振动位移K3、K2与K1的比较，可以看出K3与时变啮合刚度的参考值模型K1的最大振动位移差值不超过20%，而K2与K1的最大振动位移差值则在20%以上。可以看出K3的最大振动位移差值的百分比小于K2的百分比值，K3更加平稳。

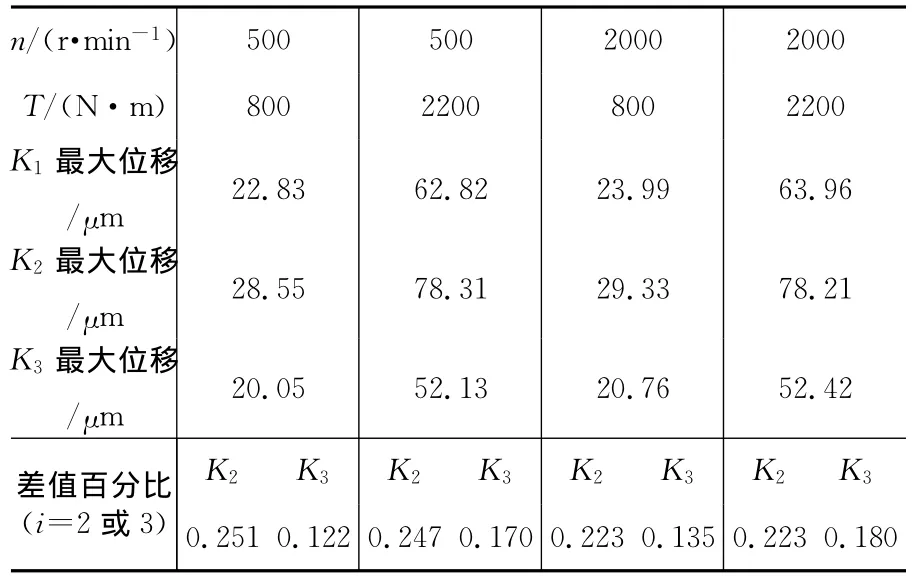
表1 不同转速和负载扭矩下最大振动位移的比较Table 1 Comparison of maximum vibration displacement under different speed and load torque condition

4.2 K1、K2、K3 的时域响应趋于稳定时间比较

由于转速和负载扭矩的大小对齿轮振动趋于稳定所用的时间影响不大，为了便于分析比较，取转速n＝500r／min、负载扭矩T＝2200N·m，比较K3和K2在不同阻尼耗散因子系数下，齿轮振动趋于稳定的时间。表2给出了3种刚度模型在不同阻尼系数下，振动趋于平衡的时间以及趋于平衡时间差值的百分比，可知K3的平衡时间更接近于K1，K3的振动趋于平衡的时间差值百分比要比K2小，尤其是在小阻尼情况下这种情况更明显。

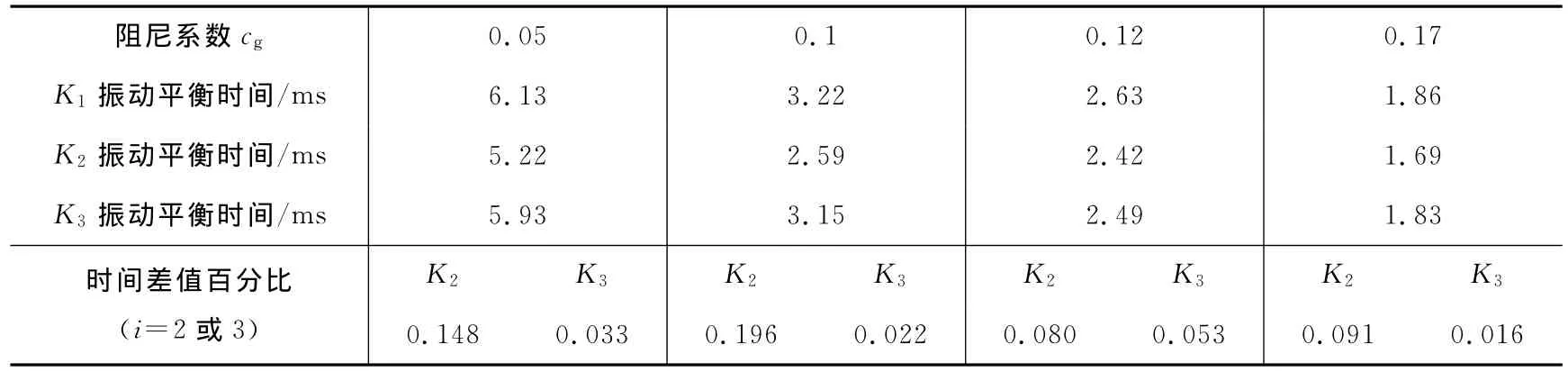
表2 在n＝500r／min和T＝2200N·m及不同阻尼耗散因子系数下趋于稳定时间的比较Table 2 n＝500r／min，T＝2200N·m，comparison of stable time under different damping coefficient

5 结 论

（1）本文基于多项式函数展开的刚度模型建立了等高齿锥齿轮动力学方程。从转速、负载扭矩、阻尼因子系数方面对基于多项式函数和基于多阶简谐波叠加函数展开的刚度模型进行仿真比较分析。

（2）基于本文方法得出的数据可以看出:基于多项式函数展开的刚度模型振动变化更加平稳。

（3）从本文方法仿真分析可知:基于多项式函数展开的刚度模型的振动变化模拟更加精确（趋于振动平衡时间差值比较小，尤其是在小阻尼的情况下），更贴近于时变啮合刚度参考值刚度模型。

［1］Song He.Effect of sliding friction on spur and helical gear dynamics and vibro－acoustics［D］.Athens:The Ohio State University，2008:24－26.

［2］Lin Jian，Parker Robert G.Mesh stiffness variation instabilities in two－stage gear systems［J］.Journal of Vibration and Acoustics，2002，124:68－76.

［3］Lin J，Parker R G.Planetary gear parametric instability caused by mesh stiffness variation［J］.Journal of Sound and Vibration，2002，249（1）:129－145.

［4］林腾蛟，蒋仁科，李润方，等.船用齿轮箱动态响应及抗冲击性能数值仿真［J］.振动与冲击，2007，26（12）:14－22.Lin Teng－jiao，Jiang Ren－ke，Li Run－fang，et al.Numerical simulation of dynamic response and shock resistance of marine gearbox［J］.Journal of Vibration and Shock，2007，26（12）:14－22.

［5］唐进元，陈思雨，钟掘.一种改进的齿轮非线性动力学模型［J］.工程力学，2008，25（1）:217－223.Tang Jin－yuan，Chen Si－yu，Zhong Jue.A improved nonlinear model for a spur gear pair system［J］.Engineering Mechanics，2008，25（1）:217－223.

［6］韩勤锴，王建军，李其汉.考虑延长啮合时齿轮副啮合刚度模型［J］.机械科学与技术，2009，28（1）:52－55.Han Qin－kai，Wang Jian－jun，Li Qi－han.A periodically time－arying mesh stiffness model for spur geared system considering the effect of extended tooth contact［J］.Mechanical Science and Technology for Aerospace Engineering，2009，28（1）:52－55.

［7］李亚鹏，孙伟，魏静，等.齿轮时变啮合刚度改进计算方法［J］.机械传动，2010，34（5）:22－26.Li Ya－peng，Sun Wei，Wei Jing，et al.Study on the improved algorithm of the time－varying meshing stiffness of gear［J］.Journal of Mechanical Transmission，2010，34（5）:22－26.

［8］刘国华，李亮玉，赵继学.考虑反向齿面啮合力的齿轮系统时变啮合刚度的研究［J］.天津工业大学学报，2006，25（6）:54－57.Liu Guo－hua，Li Liang－yu，Zhao Ji－xue.Research on time－variable－mesh－stiffness of gear pair based on inverse meshing force［J］.Journal of Tianjin Polytechnic University，2006，25（6）:54－57.

［9］郑昌启.弧齿锥齿轮和准双曲面齿轮［M］.北京:机械工业出版社，1988:312－314.

［10］屈维德.机械振动手册［M］.北京:机械工业出版社，1992.

［11］Wang Jun，Lim Teik C，Li Ming－feng.Dynamics of a hypoid gear pair considering the effects of time－varying mesh parameters and backlash nonlinearity［J］.Journal of Sound and Vibration，2007，308:302－329.

［12］李润方，王建军.齿轮系统动力学:振动、冲击、噪声［M］.北京:科学出版社，1997:156－158.

［13］Wang Jun，Lim Teik C.Effect of tooth mesh stiffness asymmetric nonlinearity for drive and coast sides on hypoid gear dynamics［J］.Journal of Sound and Vibration，2009，319:885－903.

［14］Liu Gang，Parker Robert G.Dynamic modeling and analysis of tooth profile modification for multi mesh gear vibration［J］.Journal of Mechanical Design，2008，130:1－13.

［15］朱孝录.齿轮传动设计手册［M］.北京:化学工业出版社，2005.