考虑胶层的蜂窝夹层复合材料动态特性

姜 东 江智远 费庆国 韩晓林

(东南大学土木工程学院，南京 210096)

(东南大学江苏省工程力学分析重点实验室，南京 210096)

蜂窝夹层复合材料由于其独特的结构形式，具有许多单质材料和常规复合材料所不具备的优异性能，已成为航空航天结构中不可或缺的材料之一［1］.三维实体建模方法能够模拟实际的蜂窝夹层复合材料，但建模过程复杂，计算成本过高;将蜂窝芯层等效为正交各向异性均质材料的三明治夹芯板理论在显著提高计算效率的同时保证了计算精度.国内外学者对蜂窝芯层的等效开展了大量研究［1-7］，目前主要有理论推导［1-4］、有限元计算［5］和试验分析［6］3 类方法.Gibson 等［1］以蜂窝芯层为研究对象，考虑轴向变形和剪切变形推导了正交各向异性的9个弹性参数.富明慧等［2］考虑蜂窝壁板的伸缩变形对面内刚度的影响，得到修正的Gibson公式.Xu等［3］将横向剪切变形理论引入均匀化理论中，推导了考虑面板刚度的等效弹性参数.陈玳珩等［4］提出了满足蜂窝芯与面板间位移连续条件下的等效弹性参数分析方法.Aydincak等［5］通过在蜂窝胞元模型基础上施加相应的约束和荷载来计算等效参数.Schwingshack等［6］评述了自等效理论提出以来的15种不同计算方法，并采用一种操作简便的动态试验方法测得了蜂窝夹层板的面外剪切模量.张铁亮等［7］通过对3种不同等效方法的静、动力计算结果比较，指出三明治夹芯板理论为蜂窝夹层材料等效的优选方法.在等效弹性参数分析的基础上，众多学者运用解析或数值方法针对蜂窝夹层复合材料动态特性开展了卓有成效的研究［8-10］.然而，蜂窝夹层复合材料面板与芯层一般通过胶层来粘接，而胶层对复合材料力学性能将产生重要的影响.

蜂窝夹层复合材料中胶层对结构整体性能的影响不容忽略［11］.一般情况下，胶层的力学性能远弱于面板与芯层材料，这将导致面板与芯层之间并非理想刚性连接，弱层引起的层间剪切效应将造成铝蜂窝夹层材料宏观力学性能一定程度的降低.Butukuri等［12］采用电子显微镜测量了面板与蜂窝胞壁胶接后的连接情况，并通过试验分析了胶接对蜂窝夹层复合材料平面拉伸性能的影响.Burton等［13］建立了详细的有限元模型来分析胶接接头在面板与正方形蜂窝胞壁之间荷载传递的作用和整体的静力学性能;张佳佳等［14］采用实体有限元建模的方法，分析了胶黏剂在蜂窝夹层结构变形中的作用;Tanimoto等［15］采用梁单元等效胶层与芯层，并将模态频率的计算值与试验结果进行对比，这种方法的等效过程与建模过程较复杂，而且随着蜂窝芯层高度的增加，计算精度明显降低.

本文提出了一种将面板与胶层等效为层合材料的方法，推导了其等效弹性参数;根据等效板理论、三明治夹芯板理论及本文提出的等效方法建立铝蜂窝复合材料的有限元模型，通过对比考虑胶层影响情况下蜂窝夹层复合材料动态建模的优选方法.在准确的铝蜂窝夹层复合材料有限元模型基础上，比较分析胶层参数与其他参数对铝蜂窝夹层板动态特性的影响.

1 面板-胶层等效参数

工程中通常采用三明治夹芯板理论模拟蜂窝夹层结构.假定上、下面板服从Kirchhoff假设，蜂窝芯层能抵抗横向剪切变形并且具有一定的面内刚度，忽略横向剪应力，将蜂窝芯层等效为均质且厚度与蜂窝芯高度相同的正交各项异性材料;由此将蜂窝夹层复合材料简化为上下两层面板、中间为等效芯层的三明治结构.然而，蜂窝夹层复合材料面板与芯层通过胶层粘接，一般情况下胶层的力学性能远弱于面板与芯层材料，导致面板与芯层之间并非理想刚性连接，弱层引起的层间剪切效应对夹层材料宏观力学性能有重要影响，因此，胶层对蜂窝夹层复合材料动态特性的影响不容忽略.等效板理论和三明治夹板理论都建立在将蜂窝芯层等效为正交各项异性材料基础上，而本文的方法考虑了胶层的影响.

假定面板和胶层粘接良好，可考虑为层合材料.从蜂窝夹层材料中取出长宽均为1的单元体来分析其等效弹性参数，图1为面板-胶层层合材料单元体，ts，tg分别为面板和胶层厚度.

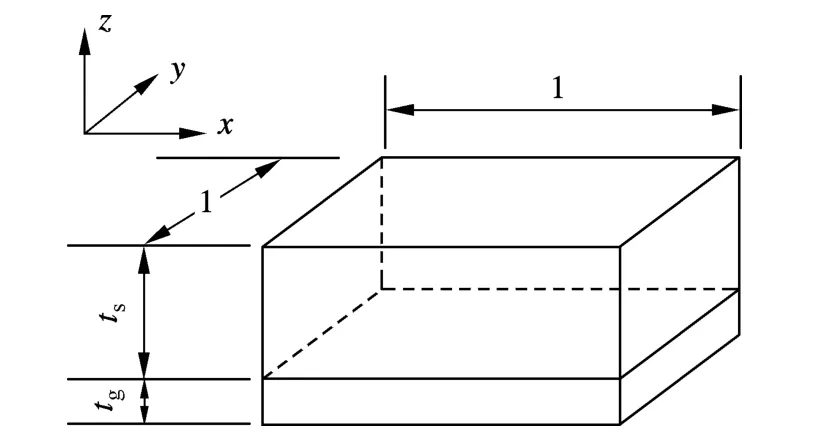
图1 面板-胶层层合材料单元体

面板和胶层的厚度远小于板的面内尺寸，两者之间黏结牢固，没有相对滑移，可以考虑为理想的弹性板.通过对材料主方向的单向拉伸来计算3个等效弹性模量，考虑x-y，x-z，y-z三个平面内的等效剪切模量.

对x，y向分别进行单轴拉伸，面板与胶层的变形相同，则

由于层合材料垂直于x轴的截面受力等于面板与胶层受力之和，即

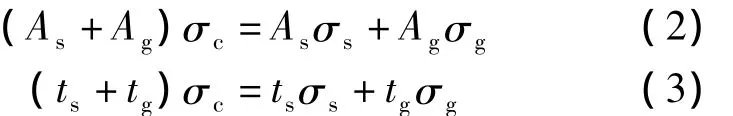
式中，σ为应力;E为弹性模量;A为截面积;下标c，s，g分别表示层合材料、面板和胶层.将式(1)代入式(3)，得到层合材料x，y向的弹性模量为

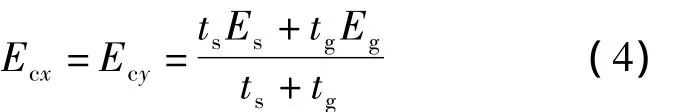
当z向进行单轴拉伸时，由于层合材料、面板、胶层垂直于z轴的应力相等，因此层合材料的位移等于面板位移与胶层位移之和，由此求得层合材料z向的弹性模量为

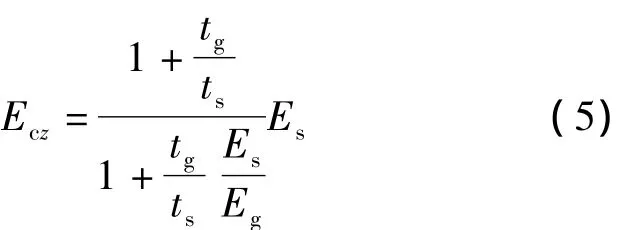
同理，对于x-y，x-z，y-z平面的纯剪切，可得到3个剪切模量

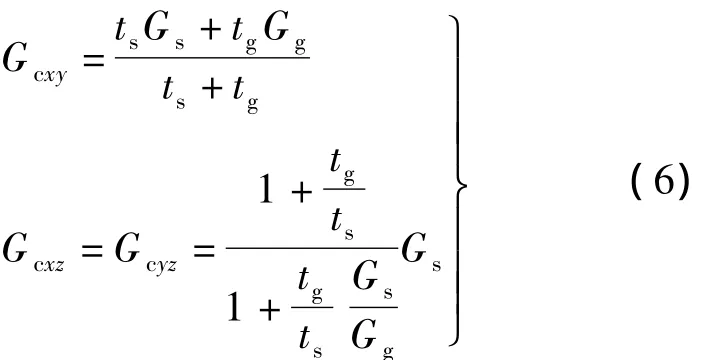
2 铝蜂窝板动态特性

铝蜂窝夹层板几何参数如图2所示，面板和芯层材料均为铝合金，弹性模量Es=68 GPa，密度为2700 kg/m3;胶层材料为环氧树脂，弹性模量Eg=5 GPa，密度为1500 kg/m3.通过自由-自由边界条件下3种有限元模型计算结果与模态试验结果的比较，来验证胶层-面板等效参数分析方法，进一步探讨适用于铝蜂窝板有限元精确建模的等效方法.

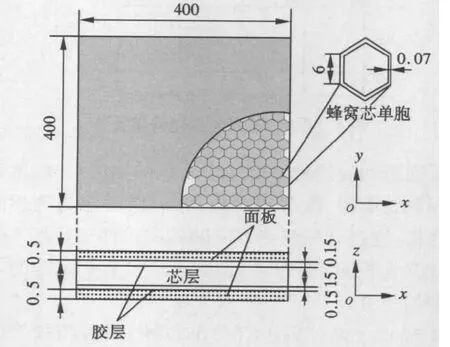
图2 蜂窝夹层板参数(单位:mm)

2.1 有限元建模

根据等效板理论、三明治夹芯板理论以及本文考虑胶层理论建立试验蜂窝夹层板的有限元模型.

1)基于等效板理论的有限元模型.根据弯曲刚度等效和拉压刚度等效将铝蜂窝夹层板等效为与之厚度不同的各向同性板，采用文献［7］中介绍的等效板理论计算的各等效参数见表1.表中，teq为等效厚度;Eeq为等效弹性模量;ρeq为等效密度;μeq为等效泊松比.

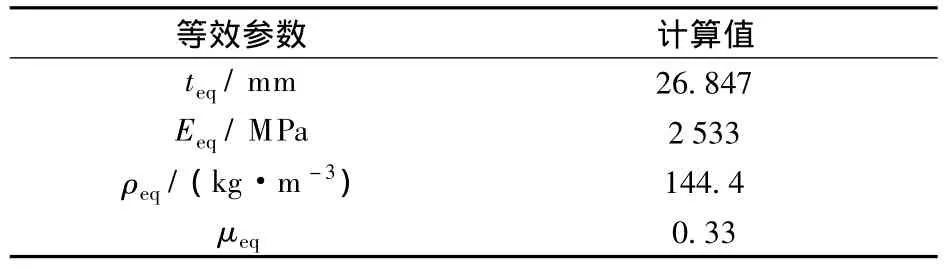
表1 等效板理论的参数

2)基于三明治夹芯板理论的有限元模型.蜂窝芯在有限元建模过程中，将铝蜂窝夹层板等效为厚度不变的正交各项异性板，各等效参数按文献［1，2，7］的理论来计算，表2为蜂窝芯层的等效参数;面板采用壳单元，芯层采用实体单元来建立有限元模型.

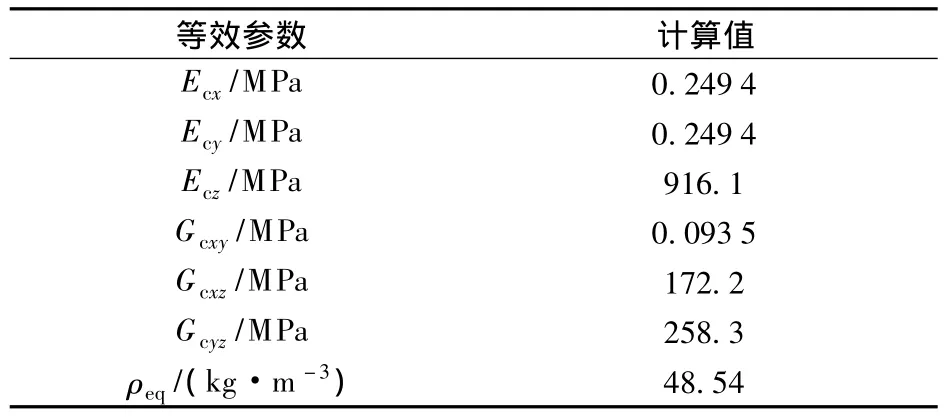
表2 蜂窝芯层的等效参数

3)考虑胶层的有限元模型.将面板与胶层考虑成厚度不变的层合材料，蜂窝芯等效为等厚度的正交各向异性材料建立有限元模型，其等效参数的计算与建模方法与2)相同.面板-胶层层合材料的等效弹性参数如表3所示.从表中可以看出，层合材料面外剪切模量与面板材料相比有较显著降低，这表明胶层在较大程度上影响材料的力学性能.

表3 面板-胶层的等效弹性参数

2.2 模态试验

试验采用锤击法，自由-自由边界条件采用尼龙绳将铝蜂窝夹层板悬挂来实现.通过铝蜂窝夹层板在自由边界条件下进行粗略的有限元建模，选择加速度传感器测点位置，避免布置在模态节点处，同时确定试验对象的大致频率范围，设置采样频率.试验频率范围为0～1000 Hz，在蜂窝板面均匀布置121个激振点，激振方向垂直于蜂窝板平面.通过模态试验，得到铝蜂窝夹层板自由边界条件前4阶模态振型和模态频率.

2.3 计算与试验结果比较

表4为不同模型的计算结果与试验值的比较.不考虑胶层影响时，等效板理论及三明治夹板理论计算得到的固有频率相对试验结果偏高，且误差均较大，等效板理论的最大误差为15.22%，三明治夹芯板理论的最大误差为9.79%;但由这2种等效理论计算得到的第2阶频率(弯曲模态)误差均较小，表明这2种等效理论仅能进行较准确的弯曲刚度等效;其他阶频率(扭转或弯扭耦合)的不准确主要是由于剪切模量的等效不准确造成的.采用本文方法考虑胶层影响后，计算精度得到较明显的提高，固有频率的最大误差降低到4.24%，平均误差也分别由10.06%和6.0%降低到2.03%，表明在对铝蜂窝板进行有限元建模时，本文方法能得到较准确的有限元模型.

通过不同模型计算与试验结果的比较表明，采用考虑胶层的影响，将面板-芯层等效为厚度不变的层合材料、芯层等效为正交各项异性材料建立的等效有限元模型，其动态特性更加准确.该方法可作为蜂窝夹层结构动态特性分析时的优选方法.

表4 固有频率计算值与试验值的比较

3 胶层对动态特性的影响

3.1 胶层参数量化分析

通过以上分析，本文提出的考虑胶层的铝蜂窝板有限元模型有更高的准确性.在此模型基础上，分别从胶层厚度、胶层材料弹性模量和密度3个方面分析胶层参数对铝蜂窝夹层板动态特性的影响，即每次计算时，仅变化其中一个参数，其他参数保持不变.胶层的初始值分别为 Eg=5 GPa，tg=0.15 mm，ρg=1500 kg/mm3.图3分别为胶层厚度、弹性模量以及密度对各阶模态频率的影响.从图中可以看出，当胶层的厚度或密度增加时，各阶固有频率也随之减小;当胶层的弹性模量增加时，各阶固有频率也随之增加.表明胶层厚度或密度与铝蜂窝夹层板固有频率负相关，胶层弹性模量则与之正相关.

3.2 灵敏度分析

以考虑胶层影响的模型为基础，通过分析铝蜂窝夹层板模态频率对各参数的灵敏度，来比较胶层参数与其他参数对铝蜂窝夹层板动态特性的影响程度.采用相对灵敏度可以消除参数数量级的影响，即

式中，Sij为相对灵敏度矩阵中的元素;fi为第i阶模态频率;pj为第j个参数.

铝蜂窝夹层板前4阶模态频率对各参数的相对灵敏度如表5所示.计算结果表明:胶层厚度和密度与模态频率负相关，胶层弹性模量与之正相关，这一结论与3.1节结论相同;各阶频率对面板厚度的相对灵敏度最高，对蜂窝芯等效体面外剪切模量Gcxz和Gcyz的相对灵敏度显著高于其他等效弹性参数，在蜂窝芯等效参数中，对动态特性影响最大的参数是剪切模量Gcxz与Gcyz;胶层参数中，除弹性模量对固有频率的影响相对较小外，厚度、密度与面板厚度和蜂窝芯面外等效剪切模量对动态特性的影响程度相当.因此，在分析铝蜂窝夹层复合材料动态特性时，胶层的影响不容忽略.

表5 铝蜂窝夹层板前4阶频率对各参数的相对灵敏度

图3 胶层参数对各阶模态频率的影响

4 结语

本文对考虑胶层影响的蜂窝夹层复合材料的动态特性进行了分析.提出了一种新的蜂窝夹层复合材料等效模拟方法.假定面板和胶层粘接良好，将面板与胶层等效为层合材料，推导了其等效弹性参数.将本文方法及2种传统等效方法的有限元模型计算结果与试验模态参数进行比较，结果表明采用考虑胶层的影响，将面板-芯层等效为厚度不变的层合材料、芯层等效为正交各项异性材料建立的等效有限元模型，其动态特性更加准确.

在铝蜂窝板准确模型基础上，分别从胶层厚度、胶层材料弹性模量和密度3个方面分析胶层参数对铝蜂窝夹层板动态特性的影响;分析结果表明，胶层厚度、密度与面板厚度和蜂窝芯面外等效剪切模量对整体动态特性的影响程度相当.考虑材料动态特性的优化设计时，胶层是重要影响因素之一，在保证面板与蜂窝胞壁连接良好的前提下，减小胶层的厚度或增加胶层材料的弹性模量能够有效提升材料的整体动态性能.

References)

［1］Gibson L J，Ashby M F.Cellular solids structure and properties［M］.2nd ed.Cambridge:Cambridge University Press，1997.

［2］富明慧，尹久仁.蜂窝芯层的等效弹性参数［J］.力学学报，1999，31(1):113-118.Fu Minghui，Yin Jiuren.Equivalent elastic parameters of the honeycomb core［J］.Chinese Journal of Theoretical and Applied Mechanics，1999，31(1):113-118.(in Chinese)

［3］Xu X F，Qiao P.Homogenized elastic properties of honeycomb sandwich with skin effect［J］.International Journal of Solids and Structures，2002，39(8):2153-2188.

［4］陈玳珩，杨璐.蜂窝板复合材料的等价弹性模量［J］.力学学报，2011，43(3):514-522.Chen Daiheng，Yang Lu.Analysis of equivalent elastic modulus of a honeycomb sandwich［J］.Chinese Journal of Theoretical and Applied Mechanics，2011，43(3):514-522.(in Chinese)

［5］Aydincak I，Kayran A.An approach for the evaluation of effective elastic properties of honeycomb cores by finite element analysis of sandwich panels［J］.Journal of Sandwich Structures and Materials，2009，11(9):385-408.

［6］Schwingshack C W，Aglietti G S，Cunningham P R.Determination of honeycomb material properties:existing theories and an alternative dynamic approach ［J］.Journal of Aerospace Engineering，2006，19(3):177-183.

［7］张铁亮，丁运亮，金海波.蜂窝夹层板结构等效模型比较分析［J］.应用力学学报，2011，28(3):275-282.Zhang Tieliang，Ding Yunliang，Jin Haibo.Comparative analysis of equivalent models for honeycomb sandwich plates［J］.Chinese Journal of Applied Mechanics，2011，28(3):275-282.(in Chinese)

［8］徐胜今，孔宪仁，王本利，等.正交异性蜂窝夹层板动、静力学问题的等效分析方法［J］.复合材料学报，2000，17(3):92-95.Xu Shengjin，Kong Xianren， Wang Benli， et al.Method of equivalent analysis for statics and dynamics behavior of orthotropic honeycomb sandwich plates［J］.Acta Materiae Compositae Sinica，2000，17(3):92-95.(in Chinese)

［9］王盛春，邓兆祥，沈卫东，等.四边简支条件下正交各向异性蜂窝夹层板的固有特性分析［J］.振动与冲击，2012，31(9):73-77.Wang Shengchun，Deng Zhaoxiang，Shen Weidong，et al.Connatural characteristics analysis of rectangular orthotropic honeycomb sandwich panels with all edges simply supported ［J］.Journal of Vibration and Shock，2012，31(9):73-77.(in Chinese)

［10］李永强，李锋，何永亮.四边固支铝基蜂窝夹层板弯曲自由振动分析［J］.复合材料学报，2011，28(3):210-216.Li Yongqiang，Li Feng，He Yongliang.Flexural vibration analysis of honeycomb sandwich plate with completely clamped support［J］.Acta MateriaeCompositae Sinica，2011，28(3):210-216.(in Chinese)

［11］王东方，杨嘉陵.含胶层复合材料梁构件性能分析［J］.航空学报，2012，33(9):1655-1663.Wang Dongfang，Yang Jialing.Analysis of the performance of a beam made of composite materials with a glue layer［J］.Acta Aeronautica et Astronautica Sinica，2012，33(9):1655-1663.(in Chinese)

［12］Butukuri R R，Bheemreddy V P，Chandrashekhara K，et al.Evaluation of skin-core adhesion bond of out-of-autoclave honeycomb sandwich structures［J］.Journal of Reinforced Plastics and Composites，2012，31(5):331-339.

［13］Burton W S，Noor A K.Structural analysis of the adhesive bond in a honeycomb core sandwich panel［J］.Finite Elements in Analysis and Design，1997，26(3):213-227.

［14］张佳佳，何景武.蜂窝夹层结构中胶粘剂的模拟和研究［J］.飞机设计，2008，28(6):27-30.Zhang Jiajia，He Jingwu.Simulation and investigation for effect of adhesive in honeycomb sandwich panels［J］.Aircraft Design，2008，28(6):27-30.(in Chinese)

［15］Tanimoto Y，Nishiwaki T，Shiomi T，et al.A numerical modeling for eigenvibration analysis of honeycomb sandwich panels ［J］.Composite Interfaces，2001，8(6):393-402.