路面激励下弹体-运输车耦合振动分析

吴邵庆 艾洪新 郭应征

(东南大学江苏省工程力学分析重点实验室，南京 210096)

(东南大学土木工程学院，南京 210096)

导弹是国防战略的重要组成部分.现代战场要求导弹等军事装备能够快速、灵活且精确打击目标，因此，导弹应具有大推力推进装置和较大长径比.弹体长径比增大使得其柔性增加，在服役过程中动力学问题也更加突出.事实上，由于振动造成结构损伤和内部仪器设备损坏的现象在弹体服役过程中较为常见.因此，弹体振动问题研究至关重要.导弹在服役前常需经过一定距离的运输;同时，为了满足战时灵活机动的要求，导弹需要具备在野外通过发射车直接发射打击目标的能力，汽车运输是最常采用的运输方式.

公路运输环境下由路面不平整引起的振动激励具有宽频、随机的特征.在由振动引起的弹体动应力水平不高的工况下，长距离公路运输仍可能引起弹体结构的疲劳损伤.因此，公路运输过程中导弹动响应水平将直接影响其服役性能.通过仿真分析准确预测运输时弹体上动响应，能够节省试验经费，缩短研究周期，具有重要的研究意义.

路面激励引起运输车辆振动，运输车振动由支撑传给弹体，弹体自身振动又会通过支撑影响运输车振动.由此，运输过程中弹体和运输车构成了一个耦合振动系统.

关于弹体等包装物公路运输已有不少研究成果.冯翔等［1］开展了固支支撑工况下导弹水平放置时弹体的固有模态分析及试验验证;许诚等［2］利用飞航导弹的有限元模型，研究了运输过程中弹体随储运箱掉落时的冲击问题;徐伟民等［3］在只考虑单层堆码且包装物与车厢捆扎(未考虑包装物与车身间支撑)工况下，建立了车辆－包装箱的动力学方程，并预示了脉冲激励作用下系统的加速度响应;李恩奇等［4］利用NASTRAN软件建立了运输车与弹体的三维有限元模型，研究了车－弹间支撑刚度对弹体振动加速度的影响，并提出减振方案;武鑫枫［5］利用模态叠加法分析了由两自由度弹簧－质量系统和其上柔性悬臂梁组成的刚柔耦合系统的振动响应，并探讨了该系统的减振控制方法;Ghaith［6］对车模型上固定的悬臂梁进行了非线性建模和动响应分析，用于模拟大型机翼结构的公路运输;Ragulskis等［7］研究了包装箱公路运输时的振动响应，建议合理的运输车速应保证路面激振频率与结构自然频率之间最大偏离.李晓刚［8］建立了以白噪声为路面激励的车辆－包装件系统的动力学模型，借助MatLab/Simulink开展了频域随机振动分析，获得了内装产品及易损零件随机振动的加速度功率谱.

本文利用欧拉－伯努利梁来模拟柔性弹体，利用有限元方法将梁模型离散后与模拟运输车的四自由度弹簧－质量系统通过自由度匹配方法建立了车－弹－刚性地面系统的耦合动力学方程.其中运输车和弹体之间的支撑采用弹簧－阻尼系统模拟，地面不平度参照国标规范［9］规定.根据建立的耦合动力学模型求解路面上行驶车－弹系统上任意部位、任意时刻的振动响应时程，并进一步探讨支撑刚度、运输车速度以及路面等级等因素对弹体设备舱部位振动量级的影响，为运输过程中弹体的动响应分析、振动控制以及安全性评估提供参考.

1 车-弹耦合动力学模型

1.1 弹体动力学模型

导弹多为具有较大长径比的柔性结构.采用如图1所示欧拉－伯努利梁来模拟其动力学特性.弹体梁模型的动力学方程为

式中，ρA，c和EI分别为梁结构的线密度、阻尼以及抗弯刚度;u(x，t)为梁上x处t时刻的位移响应;F1(t)，F2(t)分别为运输车与弹体间的支撑力;li为第i个支撑与弹体左端点的距离.本文为了动力学模型的推导方便，只考虑包含2个支撑的情况，对于多个支撑情况下的动力学方程可通过类似的推导得出.

图1 弹体梁模型

采用梁单元离散弹体模型，可得如下有限元模型:

式中，Ms，Cs和Ks分别为弹体结构的质量矩阵、阻尼矩阵和刚度矩阵，本文采用瑞利阻尼模型，则有Cs=α0Ms+α1Ks，其中，α0和 α1为常数;分别为梁模型的节点位移、速度和加速度向量;Hs为梁模型上支撑与弹体间相互作用力的位置矩阵，且有

式中，N为考虑边界条件时梁模型的自由度数;NP为支撑处相互作用力的个数，本文取NP=2;Hi为第i个力所作用梁单元的形函数，表示为

式中，L为弹体总长度;l1为第1个支撑到弹体左端点距离;l2为第2个支撑到弹体左端点距离;g为重力加速度.

1.2 运输车动力学模型

本文采用如图2中所示的四自由度弹簧－质量系统来模拟运输车的动力学特征.尽管运输车辆一般都为多轴挂车，但采用两轴的车模型在推导其耦合振动方程时并不失一般性.图中，F'1(t)，F'2(t)为支撑对运输车的作用力;F3(t)，F4(t)为地面对轮胎的作用力;L0为弹体与运输车间两支撑的距离;S为车轴距;a1，a2为分配系数;y3，y4分别为梁模型上两支撑处的位移.

图2 运输车模型

根据能量法，利用Lagrange方程可以推导运输车辆的动力学方程为

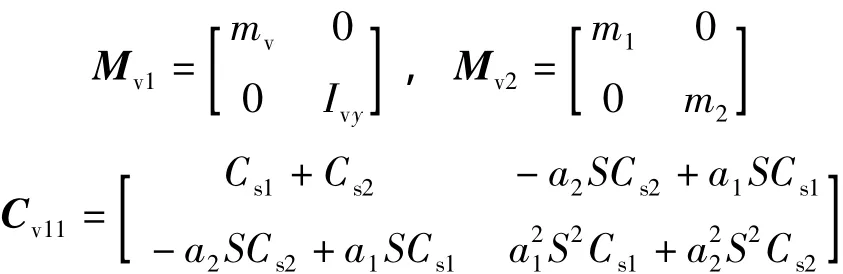
1.3 车-弹耦合动力学模型

将弹体有限元模型和运输车动力学模型通过支撑处自由度匹配，建立车－弹耦合振动系统动力学方程，即

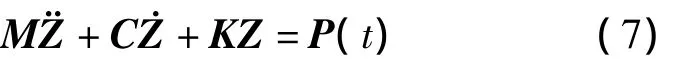
其中，r(x1)，r(x2)分别为两车轮作用处的路面粗糙度;r'(x)=表示路面粗糙度函数对空间位置的一阶导数表示第i个轮子位置对时间的一阶导数.

1.4 路面粗糙度

在GB7031—86规范［9］中，路面粗糙度功率谱密度由下式定义:

式中，n0为参考空间频率，n0=0.1 m－1;n为空间频率，m－1，n=f/v，f为时间频率，v为车速;Gd(n0)为在参考空间频率n0下的路面功率谱值，称为路面不平度系数，Gd(n0)取 16×10－6，64×10－6，256 ×10－6和 1024 ×10－6m3，分别对应 A，B，C和D级公路;w为频率指数，决定路面谱的频率结构，一般取w=2.

根据规范中给出的路面位移功率谱密度，路面粗糙度随空间变化的函数r(x)可以表示为［10］

式中，θk为一组在0～2π之间服从均匀分布的随机相位;Gd(fmid，k)为将功率谱的时间频率划分为n1个小区间，每个小区间的中心频率fmid，k处的谱密度值，且

可以证明，由一系列包含随机相位的简谐成分叠加而成的粗糙路面剖面样本服从高斯分布，且每个样本都可以能够准确反映式(8)中给出的功率谱密度，具有各态历经的性质.

2 数值仿真

2.1 车-弹模型参数

弹体、运输车模型参数如表1所示.

将弹体支撑假设为弹性支撑，在支撑处未加装阻尼器工况下，其阻尼较小，在本研究中假设支撑阻尼忽略不计，即C1=C2=0;当两支撑刚度分别为K1，K2时，根据车－弹耦合模型中弹体自由度对应的质量、刚度子矩阵的特征值获得带支撑约束弹体梁模型的固有频率.由于在车－弹模型动力学模型推导过程中包含阻尼项，因此，当支撑阻尼不为零时，本文的分析方法也同样适用.假设弹体梁模型前两阶模态阻尼比为0.02，利用带支撑梁模型的前两阶固有频率计算弹体梁模型的瑞利阻尼系数.利用Matlab编写计算程序，采用Newmark－β法求解方程(7)，对不同工况下车－弹耦合振动系统动响应进行分析.路面不平度曲线可根据式(10)计算.由于设备舱部位对振动量级要求苛刻且位于弹头附近，本研究中假设弹体梁模型右侧第1个单元中左侧节点位置为设备舱部位，并定义为弹体上重点部位.

表1 车－弹模型参数

2.2 支撑刚度对弹体动响应的影响

支撑条件对弹体上振动量级、动应力分布等有一定影响.工程中需要设计合理的支撑刚度，以降低弹体各部位处振动量级.将运输车－弹体间的2个弹性支撑刚度取相同值，分析运输车以10 m/s速度在B级公路上行驶时，弹体上重点部位处位移、加速度随支撑刚度的变化规律，如图3所示.

弹体支撑刚度过小会引起弹体运动位移过大，在设计时应该予以避免.由图3可知，支撑刚度过小时弹体振动位移很大，随着支撑刚度增大，弹体上重点部位处振动位移均方根减小并趋于稳定;振动加速度均方根随支撑刚度增加呈先增后减然后缓慢增加，最后趋于稳定的变化趋势，与文献［5］中得出的规律一致.当支撑刚度较小(如小于8.0 MN/m)时，弹体加速度均方根随支撑刚度增大而增大，其原因为支撑刚度增大使得车辆的振动能够更好地传递给弹体，同时路面激励使得车－弹系统在多模态发生共振，引起弹体加速度均方根出现峰值;随着刚度的进一步增大，共振现象减弱，加速度均方根出现谷值，本工况下，当支撑刚度K1=K2=37 MN/m时，重点部位处加速度均方根出现最小值(3.92 m/s2);之后当支撑刚度继续增大至102MN/m量级时，加速度均方根逐渐收敛趋于稳定，此时，支撑呈现刚性，弹体与车身的振动量级接近.综合考虑弹体重点部位的振动位移和振动加速度随支撑刚度的变化情况，在本工况下，K1=K2=37 MN/m为支撑刚度的最优值.

图3 弹体重点部位动响应随支撑刚度变化规律

2.3 车速对弹体动响应的影响

运输车行驶速度对弹体振动量级也有较大影响.考虑运输车在B级公路上行驶，分析不同车速工况下，弹体上重点部位处的动响应.图4给出了车速v=10 m/s时弹体重点部位处的位移、速度和加速度时程.

图5中给出了弹体设备舱部位的位移、速度和加速度均方根随车速变化的曲线.可以看出，弹体设备舱处的位移、速度和加速度均方根随车速增大呈波动增大的趋势.其原因在于，随着车速增加，由路面激励F3(t)，F4(t)的表达式可知，路面激励对车－弹系统的激振频率上限会提高，且激振能量分布随着速度变化而变化.当车速增大时，激振频率上限提高引起位移响应增大，同时在系统位移响应中增加更多的高频成分，即位移变化加快，引起速度和加速度均方根增大.根据车－弹系统固有特性分析，其频响函数在中低频范围内有较多峰值，当然路面激励频谱各峰值与系统频响函数各峰值重叠较多时，会引起动响应均方根呈现局部最大值.当车速继续增大，在一定范围内激励和频响的峰值又会错位，引起动响应均方根的减小，从而形成如图5所示动响应均方根波动上升的曲线.

图4 B级公路上车速v=10 m/s时弹体重点部位处动响应

图5 B级公路上车速对重要部位处动响应均方根的影响

2.4 路面等级对弹体动响应的影响

路面不平整是车－弹系统的主要激振源，研究路面状况对弹体动响应的影响非常必要.取运输车的行驶速度为10 m/s，路面等级取国标规范［9］中的A，B，C，D级4个等级，分别代表路面状况好、一般、不好、差4种工况进行分析.

图6中给出了C级公路上以10 m/s速度行驶的运输车上弹体重点部位处动响应时程.对比图4和图6中结果可知，运输车以相同速度(10 m/s)行驶时，随着路面状况的恶化(由B级公路变为C级公路)，弹体重点部位处的竖向振动位移、速度和加速度幅值明显增大;表2给出了运输车以相同速度(10 m/s)行驶在不同等级路面上时，弹体上重点部位处的振动位移、速度、加速度均方值(RMS值).可以看出，路面状况的好坏，对于弹体的运输振动环境有很大的影响，较差路况导致的弹体振动以及其内部动应力和变形更容易引起弹体结构和内部仪器的损坏.

图6 C级公路上车速v=10 m/s时弹体重点部位处动响应

表2 不同路面等级下弹体重点部位振动响应均方根

3 结论

本文对导弹在公路运输过程中的振动问题进行模拟.利用有限元和能量法推导了路面激励下车－弹系统的耦合动力学方程，并利用Matlab编程实现了路面激励输入模拟以及路面激励下运输车上弹体重点部位处振动量级的定量分析，为导弹运输的减振设计和安全评估提供理论分析手段.

利用数值仿真分析了支撑刚度、运输速度以及路面等级等因素对弹体上设备舱部位振动水平的影响，得出如下结论:

1)弹体上设备舱部位振动位移均方根随支撑刚度增加而减小并趋于稳定.

2)弹体振动加速度均方根随支撑刚度增加呈现先增后减然后缓慢增加最后趋于稳定的变化趋势.当支撑刚度较小时，弹体加速度均方根随刚度增大而增大，其原因为支撑刚度增大使得车辆振动能够更好传递给弹体，同时路面激励使得车－弹系统在多模态发生共振，引起弹体加速度均方根出现峰值;随着支撑刚度进一步增大，共振现象减弱，加速度均方根出现谷值;再继续增大支撑刚度，加速度均方根缓慢增加后趋于稳定，此时，支撑呈现刚性，弹体与车身的振动量级接近.

3)弹体上位移、速度和加速度均方根随运输车速增大呈波动增大的趋势.

4)随着路面状况的恶化，弹体上的振动位移、速度以及加速度都会有明显增大.路面状况的好坏，对于弹体运输振动环境有很大影响，较差路况导致的弹体振动以及其内部动应力和变形更容易引起弹体结构和内部仪器的损坏.

References)

［1］冯翔，李向斌，关正西，等.运输环境中某战术导弹结构振动特性分析［J］.固体火箭技术，1999，22(1):1－11.Feng Xiang，Li Xiangbin，Guan Zhengxi，et al.Finite element structure vibration characteristic analysis of a solid missile in transportation environment［J］.Journal of Rocket Technology，1999，22(1):1－11.(in Chinese)

［2］许诚，侯志强，李善高，等.飞航导弹在运输过程中的动力学计算［J］.兵工学报，2002，23(2):219－223.Xu Cheng，Hou Zhiqiang，Li Shangao，et al.Calculation on dynamic characteristics of the fuselage of winged missiles during their transportation［J］.Acta Armamentarii，2002，23(2):219－223.(in Chinese)

［3］徐伟民，孙国正.路面脉冲激励下汽车运输包装产品响应的数值仿真［J］.包装工程，2004，25(4):163－165.Xu Weimin，Sun Guozheng.Numerical simulation of packaging product dynamic response under road pulse excitation［J］.Packaging Engineering，2004，25(4):163－165.(in Chinese)

［4］李恩奇，唐国金，雷勇军，等.X型固体导弹公路运输随机响应分析与减振方法［J］.暨南大学学报;自然科学与医学版，2005，26(1):50－54.Li Enqi，Tang Guojin，Lei Yongjun，et al.Response analysis of X missile during road transportation and investigation of the vibration control system［J］.Journal of Jinan University:Natural Science＆Medicine Edition，2005，26(1):50－54.(in Chinese)

［5］武鑫枫.车载刚柔耦合系统建模与减振控制［D］.合肥:中国科技大学信息科学技术学院，2011.

［6］Ghaith F A.Nonlinear dynamic modeling of elastic beam fixed on a moving cart and carrying a lumped tip mass subjected to external periodic forces［C］//Proceedings of the ASME 2009 International Design Engineering Technical Conferences ＆ Computers and Information in Engineering Conference.San Diego，California，USA，2010:935－941.

［7］Ragulskis K，Gegeckienë L，Kibirkštis E，et al.Dynamic study of transportation containers with packages［J］.Journal of Vibroengineering，2012，14(4):1876－1884.

［8］李晓刚.运输包装系统随机振动频域分析［J］.包装工程，2012，33(15):50－54.Li Xiaogang.Random vibration frequency domain analysis of transport packaging system［J］.Packaging Engineering，2012，33(15):50－54.(in Chinese)

［9］中国国家标准化管理委员会.GB7031—86车辆振动输入、路面平度表示方法［S］.北京:中国标准出版社，1986.

［10］段虎明，石峰，谢飞，等.路面不平度研究综述［J］.振动与冲击，2009，28(9):95－101.Duan Huming，Shi Feng，Xie Fei，et al.A survey of road roughness study［J］.Journal of Vibration and Shock，2009，28(9):95－101.(in Chinese)

［11］Wu S Q，Law S S.Vehicle axle load identification on bridge deck with irregular road surface profile［J］.Engineering Structures，2011，33(2):591－601.