基于单层纤维失效准则的FRP型材-混凝土组合梁极限承载力计算与试验
王景全 李嵩林 吕志涛
(1东南大学混凝土与预应力混凝土教育部重点实验室,南京 210096)
(2东南大学国家预应力工程技术研究中心,南京 210096)
(3招商局重庆交通科研设计院有限公司,重庆400067)
FRP型材-混凝土组合梁是一种理想的桥梁结构形式,具备轻质、高强、耐久的特点,能充分发挥FRP高强抗拉性能和混凝土的抗压性能[1-5].FRP型材-混凝土组合梁的破坏模式具有多样性,主要体现在以下3个方面:①FRP复合材料具有各向异性和高强线弹性,与钢材、混凝土材料性能迥异,故FRP型材-混凝土组合梁的受力性能与传统结构的差别较大;② FRP纤维含量及纤维铺层方式的多样性对其力学特性影响显著;③ FRP构件制作工艺的多样性对其力学特性有直接影响.FRP型材-混凝土组合梁主要有7种失效模式:FRP腹板纵向层间剪切破坏[6]、FRP 腹板屈曲[7]、FRP 翼板材料强度破坏[8]、混凝土压碎致弯曲破坏[9]、扭转失稳破坏[10]、界面黏结失效[11]和混凝土板剪切破坏[11].
FRP型材-混凝土组合梁破坏模式的多样性给设计带来了诸多计算难题.若逐一对每种破坏模式进行验算,势必加大该结构形式设计工作的复杂程度.为此,本文从复合材料细观力学层次上,提出了一种基于FRP单层纤维失效准则的组合梁极限承载力计算方法,以涵盖由FRP型材强度失效引起的各种失效模式.对于混凝土桥面板的破坏模式,可借鉴现有规范方法[12]进行计算,不再赘述.
1 组合梁截面和单层纤维受力
FRP型材强度失效的判定过程如下:① 计算截面的应力(正应力、剪应力、剪切变形引起的附加正应力);② 计算FRP型材各板条(翼板和腹板)的面内荷载;③ 计算各板条单层纤维的应力;④利用复合材料的失效准则判定是否失效.
FRP翼板承受的应力由2个部分组成,即弯曲变形引起的正应力σ和剪切变形引起的附加正应力Δσ.FRP腹板承受的应力亦由2个部分组成,即弯曲变形引起的正应力σ和剪应力τ.为便于分析,假设组合梁界面有可靠的连接,不考虑FRP梁与混凝土板之间的滑移和掀起效应.
1.1 截面附加正应力的计算
宽翼缘的薄壁梁截面剪切变形引起的截面附加正应力Δσ不可忽略,且附加正应力的大小与材料的弹性模量和剪切模量的比值成正比[13].典型的国产树脂基复合材料HT3/QY8911(高强碳纤维/双马)的纵向弹性模量为135 GPa,面内剪切模量为4.5 GPa,两者之比约为30,而对于传统材料如钢材,该值仅为2.6.显然,复合材料的弹性模量与剪切模量的比值远大于钢材,故由剪切变形引起的附加正应力Δσ不可忽略.
Δσ的求解思路如下:①根据材料力学方法,得出截面剪应力分布;②计算任意截面高度处剪切变形引起的梁截面轴向变形;③将剪切变形引起的梁截面轴向变形等效为截面附加正应变;④由正应力与应变的关系,得到截面附加正应力的大小.
以承受均布荷载q作用的FRP工字型截面简支梁为分析对象(见图1).截面上剪应力的分布如图2所示.图中,τxy,τxz分别表示垂直于 x轴的某一截面上y方向和z方向上的剪应力.在图2中,取一微元体dA,可得剪应力τ引起的剪切变形.

图1 承受均布荷载的FRP工字梁

图2 截面剪应力分布
图3为1/2截面的剪切变形图.由图可知,由ABCDE截面变形为A'B'C'D'E'截面时,引起了附加轴向变形.将剪切变形引起的梁截面轴向的位移u等效为截面附加正应力引起的轴向变形.
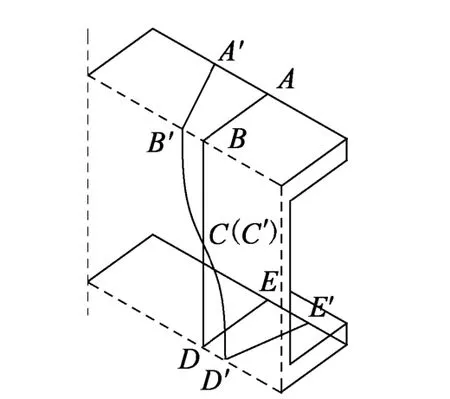
图3 截面剪切变形图
距中和轴y处的附加应力Δσx可表示为[13]

式中,Ex为材料沿x方向的弹性模量;Q为梁计算截面的剪力;S为y位置处截面对中性轴的静矩;Iz为组合梁的截面惯性矩;Gxy为复合材料在xoy平面内的剪切模量;t为附加正应力位置处截面的宽度.
若对等截面梁的材性沿截面高度不变,即Gxy,Iz均为常数,则截面上承受的剪力Q与截面高度无关,式(1)可简化为
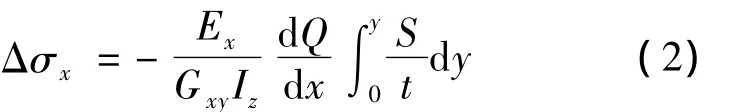
对于跨中集中荷载F作用下的简支组合梁,任意截面处剪力Q=F/2为常数,dQ/dx=0,故附加正应力为0.对于承受均布荷载q的简支组合梁,任意截面处剪力 Q=ql/2-qx,则 dQ/dx=-q,故式(2)可进一步简化为

1.2 FRP翼板单层纤维的细观力学计算
工字型FRP梁翼缘板的纤维主要沿纵向0°铺层,故可基于经典层合板理论计算其应力.
外荷载作用下,在跨内取任意截面(见图4).FRP梁下翼板承受的应力由2个部分组成,即弯曲变形引起的正应力σ和剪切变形引起的附加正应力Δσ.由剪力引起的截面剪应力τ可忽略不计(见图5).图中,hf为组合截面换算后FRP翼板的厚度.
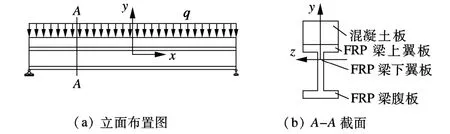
图4 组合梁跨及截面布置

图5 FRP梁下翼缘应力分布
在FRP下翼板中取出一块平面尺寸为1×1、高度为hf的单元体,则该单元体上承受的面内荷载如图6所示.图中,Nx,Nz分别为FRP梁翼板承受的面内纵向、横向拉力(或压力);Nxz为FRP梁翼板承受的面内剪力.
面内荷载计算表达式为
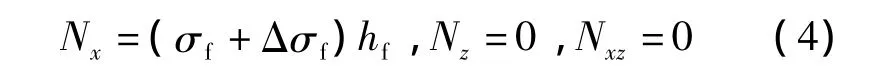
式中,σf,Δσf分别为由组合梁弯曲变形引起的FRP梁翼板最大正应力和最大附加正应力.

图6 翼板单元体承受的面内荷载
单层树脂基复合材料主方向刚度系数为

式中,Q11,Q22分别为纵向、横向抗拉刚度;Q12为纵横向泊松比效应对刚度系数的影响值;Q66为xoz面内剪切刚度系数;EL,ET分别为树脂基复合材料的纵向、横向拉伸模量;GLT为复合材料的面内剪切模量;νLT,νTL分别为树脂基复合材料纵向、横向泊松比,且 νLTEL=νTLET.
由h层0°纤维铺叠成的单向层合板的刚度系数 Aij(i=1,2,6;j=1,2,6)可表示

由此可得翼板的面内刚度矩阵为

翼板面内的柔度矩阵a为

翼板竖向对称轴处的应变为

翼板单层在参考坐标系下的应力为

式中,σx,σy分别为 x,y 方向上的应力值;τxy为面内剪切应力.
FRP工字梁翼缘板各单层纤维在材料主方向上的应力为

式中,σL,σT分别为翼板纵向、横向应力值;τLT为面内剪切应力.
1.3 FRP腹板单层纤维的细观力学计算
根据FRP梁的受弯特性,FRP腹板主要承受剪力,故主要布置±45°纤维铺层.下面讨论FRP腹板各单层主方向上的应力计算.
在外荷载作用下,FRP腹板某一高度处承受的面内荷载为
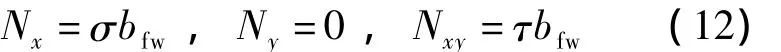
式中,bfw为FRP腹板的宽度;Ny为FRP腹板承受的横向拉力或压力;Nxy为FRP腹板面内剪力.
由式(5)可以求出单层纤维主方向上的刚度系数Qij.±45°纤维铺层方式下单层材料沿梁参考坐标系下的刚度系数(i=1,2,6;j=1,2,6)与Qij的关系可表示为

对于±45°铺层的对称层合板,其刚度系数Aij(i=1,2,6;j=1,2,6)可按下式计算:
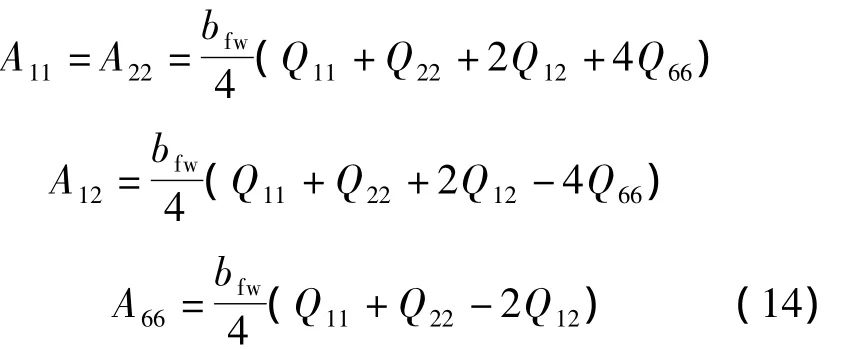
由此可得FRP腹板的面内刚度矩阵为

则腹板面内的柔度矩阵与式(9)相同.
腹板竖向对称轴处的应变为

腹板单层在参考坐标系下的应力为

45°纤维铺层的翼板各单层在材料主方向上的应力为
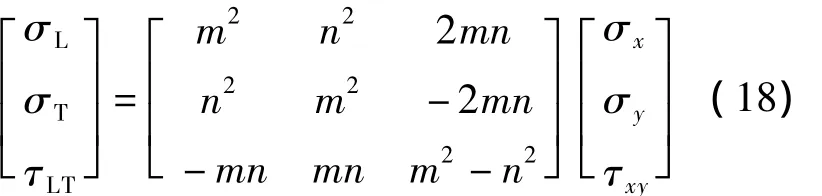
2 组合梁极限承载力计算
2.1 FRP梁上翼缘单层纤维失效的计算模型
FRP上翼缘单层纤维失效对应的组合梁极限破坏现象为FRP梁上翼缘受压破坏,应满足复合材料单层的最大应力准则,其对应的承载力计算模型为

式中,Xc为单层纤维沿纤维方向的压缩强度.
2.2 FRP梁下翼缘单层纤维失效的计算模型
FRP梁下翼缘单层纤维失效对应的组合梁极限破坏现象为FRP梁下翼缘受拉破坏,应满足复合材料的最大应力准则,其对应承载力计算模型为

式中,Xt为单层纤维沿纤维方向的拉伸强度.
2.3 FRP梁腹板单层纤维失效的计算模型
单层纤维强度破坏应满足复合材料单层的最大应力准则,其对应的承载力计算模型为

单层纤维主方向强度破坏应满足复合材料单层的最大应力准则,其对应的承载力计算模型为

式中,Yt,Yc分别为单层纤维垂直纤维方向的拉伸强度和压缩强度.
单层纤维在复合应力状态下的强度破坏,应同时满足复合材料单层的最大应变准则和Tsai-Wu张量多项式准则,其对应承载力计算模型为

式中,Fx,Fy,Fxx,Fxy,Fyy,Fss为复合材料强度参数[13],通过强度试验得到,限于篇幅不赘述.
3 试验验证
3.1 试件参数
为验证本文提出的FRP型材-混凝土组合梁极限承载力计算方法的可靠性,对3根跨径2600 mm、梁高300 mm的FRP型材-混凝土组合梁进行了试验,界面采用钢螺栓剪力键连接.组合梁截面及立面如图7所示.

图7 试验梁尺寸图(单位:mm)
3.2 试验装置
试验加载装置如图8所示.由一个20 t的油压千斤顶实施三分点加载,并采用15 t的BHR-4型称重传感器测力.试验测量数据包括跨中位移、支座位移、混凝土板和FRP梁相对滑移、混凝土和FRP梁应变以及荷载值.试验加载由荷载控制,按每级0.5 kN加载.

图8 试验现场照片
3.3 试验结果分析
表1列出了试验梁极限承载力、破坏模式的试验结果与理论分析结果.

表1 试验结果与理论计算结果的对比
由表1可知,根据本文方法计算得到的FRP型材-混凝土组合梁的极限状态为FRP主梁腹板破坏,极限荷载值与试验结果吻合良好.
4 结论
1)FRP复合材料的特性、铺设方式、制造工艺以及界面连接等对FRP型材-混凝土组合梁结构性能的影响,使得FRP型材-混凝土组合梁的失效模式呈现多样性.
2)提出了简单区分2类破坏形式的计算思路,有效简化了结构计算的复杂性.从复合材料细观力学层次上,建立了基于FRP单层纤维失效准则的组合梁极限承载力计算方法,可涵盖由FRP型材强度失效引起的各种失效模式.
3)根据所提方法得到的计算结果与3片FRP型材-混凝土组合梁的试验结果吻合良好,说明该方法能够较好地预测组合梁的极限承载力和破坏类型.
References)
[1]叶列平,冯鹏.FRP在工程结构中的应用与发展[J].土木工程学报,2006,39(3):24-36.Ye Lieping,Feng Peng.Applications and development of fiber-reinforced polymer in engineering structures[J].Chinese Civil Engineering Journal,2006,39(3):24-36.(in Chinese)
[2]张普,朱虹,孟少平,等.混杂FRP-混凝土T形组合梁受弯性能试验研究[J].东南大学学报:自然科学版,2010,40(3):548-553.Zhang Pu,Zhu Hong,Meng Shaoping,et al.Experimental study on bending performances of hybrid FRP-concrete composite T-beams[J].Journal of Southeast University:Natural Science Edition,2010,40(3):548-553.(in Chinese)
[3]Nikola D,Thanasis C T,Urs M.Innovative design of FRP combined with concrete:short-term behavior[J].Journal of Structural Engineering,ASCE,1995,121(7):1069-1078.
[4]Manalo A C,Aravinthan T,Mutsuyoshi H,et al.Composite behaviour of a hybrid FRP bridge girder and concrete deck[J].Advances in Structural Engineering,2012,15(4):589-600.
[5]Chen Y,Zidhl H,Kenneth W H.Experimental characterization and optimization of hybrid FRP/RC bridge superstructure system [J].Journal of Bridge Engineering,ASCE,2009,14(1):45-54.
[6]Gordon P W,Amjad J A.Sustained-load and fatigue performance of a hybrid FRP-concrete bridge deck system[J].Journal of CompositeforConstruction,ASCE,2010,14(6):856-864.
[7]Nguyen D H,Hiroshi M,Shingo A,et al.Structural behavior of hybrid FRP composite I-beam[J].Construction and Building Materials,2010,24:956-969.
[8]陈志涛.FRP型材-混凝土组合梁桥受弯性能的试验与理论研究[D].南京:东南大学土木工程学院,2012.
[9]Kavlicoglu B M,Gordaninejad F,Saiidi M,et al.Behavior of a graphite epoxy concrete bridge girder[J].Composites Part B:Engineering,2006,37(2/3):171-181.
[10]Hulatt J,Hollaway L,Thorne A.Short term testing of hybrid T-beam made of new prepreg material[J].Journal of Composites for Construction,ASCE,2003,7(2):135-144.
[11]Nordin H,Taljsten B.Testing of hybrid FRP composite beams in bending[J].Composites Part B:Engineering,2004,35(1):27-33.
[12]中华人民共和国住房和城乡建设部.GB50608—2010纤维增强复合材料建设工程应用技术规范[S].北京:中国计划出版社,2010.
[13]王兴业.复合材料力学分析与设计[M].长沙:国防科技大学出版社,1999.

