数字图像相关方法中的标定对三维形貌和变形测量的影响
陈振宁 刘 聪 何小元
(东南大学土木工程学院,南京 210096)
(东南大学江苏省工程力学分析重点实验室,南京 210096)
近年来,随着光电技术和计算机的快速发展,数字图像相关方法[1-4](digital image correlation,DIC)、电子散斑干涉法、相移法、时间序列法等高精度、非接触、无损伤的现代光测实验力学方法[5]逐步走向数字化和自动化.而数字图像相关方法以其全场测量、现场可测等特点备受关注,其在土木工程、交通运输等科学领域的应用得到学者们的普遍关注[6].
数字图像相关方法是一种基于光电成像和计算机数字处理的测量技术,对相机成像质量要求较高.而相机成像是基于针孔成像模型的,对成像元件内部参数进行标定是必不可少的步骤.对于双相机三维DIC系统,同时要标定2个相机间的相对位置和内部参数才能确定空间中的被测物体位置.因此,标定成为三维DIC系统中关键的步骤.由于实际工程测量现场的复杂性,标定过程很随意,使得标定结果不精确,从而影响测量精度.针对上述问题,本文研究了棋盘标定板的姿态,考察了标定结果的稳定条件,从而优化标定过程.
1 数字图像相关方法
由于散斑的随机性,物体上计算点周围小区域(通常称为子区或者模板)的斑点分布是各不相同的,假设变形前后物体同一个点的灰度不变,因此,若计算点未超出图像范围,可以认为子区中的计算点在变形后的图像中唯一存在[7].设子区变形前图像灰度为f(x,y),变形后的图像子区灰度为g(x,y),根据相关函数进行一定的相关搜索即可得到目标点变形后的位置.常用的衡量公式归一化的相关函数C表达式[2]为
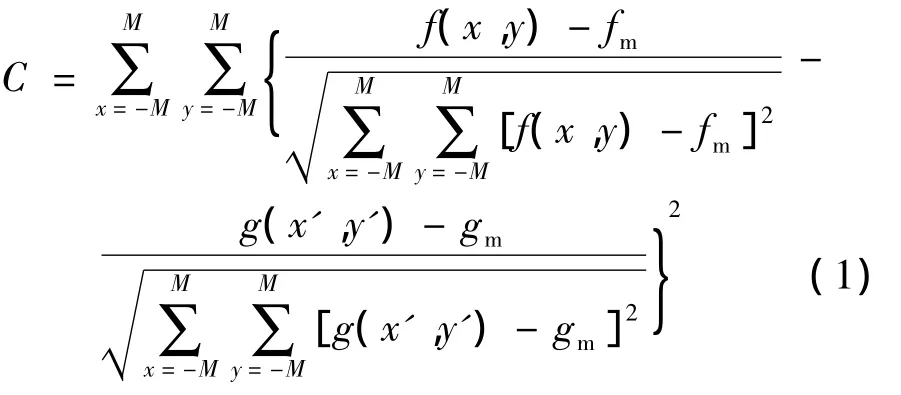
式中,(2M+1)×(2M+1)为子区的大小;fm,gm分别为参考子区和搜索子区的平均灰度值.运用相关搜索使得C达到最大值.为了获得亚像素精度,需要在进行整像匹配的基础上进行亚像素估计.图1为一个点的相关搜索示意图,对于参考子区中任一点,可在目标子区搜索到该点的位置.
由于单相机的二维相关方法不能保证相机绝对垂直于试件表面,同时,二维数字图像相关方法对试件表面要求苛刻,降低了该方法的测量精度.因此,基于双目立体视觉原理和三维匹配等技术的三维DIC被应用到物体的三维形貌、位移、应变等物理量的测量中[4,8].下面将介绍相机成像模型,引入双目立体视觉原理,对三维双相机DIC的系统进行标定.

图1 相关搜索示意图
2 相机模型与三维标定原理
2.1 针孔相机模型
一般情况下,可用理想针孔模型描述相机成像原理.相机成像的几个常用坐标系为世界坐标系W-XYZ、相机坐标系C-XcYcZc和图像坐标系I-xy.
由于相机靶面不一定与被测平面平行,并且工艺制造也存在误差,要获得高精度的测量结果,首先需要知道相机坐标系和世界坐标系之间存在平移和旋转关系.设空间中任意一点P的世界坐标为 X={X,Y,Z}T,在相机坐标系中为 Xc={Xc,Yc,Zc}T,则有以下方程:

式中,R为3×3旋转矩阵,其独立变量为3个旋转角,可以用旁向倾角ω、航向倾角φ和图像旋角κ表示;t为3×1平移向量,有3个独立分量 tx,ty,tz.称参数 ω,φ,κ,tx,ty,tz为每个成像相机的 6 个外部参数.

则点P在相机内成像表示为

式中,Cx,Cy为光轴与成像平面交点的图像坐标,即为图像主点.称参数 Cx,Cy,fx,fy为相机内部参数.将式(2)~(4)写成如下矩阵的形式:
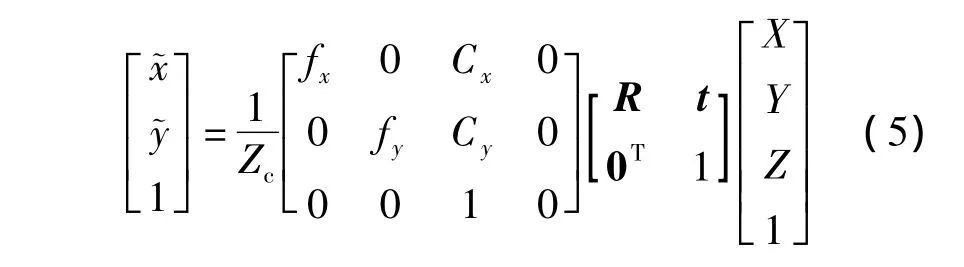
在棋盘标定中,通常把世界坐标系建立在标定板的表面,坐标原点放到第一个内角点处.
2.2 镜头畸变
由于工艺的复杂性和生产误差,镜头存在畸变使得实际像点与理想点存在像差,尤其是广角镜头.在高精度测量中,必须进行镜头的畸变校正[9-11].上述未经校正的理想成像点为~x,设~x校正后的成像点x=(x,y),校正畸变的成像点可表述为

式中,δ=(δx,δy)为像差向量(包括径向像差和切向像差),是由镜头畸变引起的.像差模型有多种,切向畸变的影响相对较小,因而将径向畸变作为镜头畸变的主要影响因素[11].由镜头径向畸变引起的点A变形前后的成像误差如图2所示,假设δ1,δ2为变化前后点A的畸变像差,点A实际发生的变形为dAB,由于畸变的存在,成像变形为dA'B'.

图2 镜头径向畸变引起的误差
因此,可以用下面的畸变形式表述[12]:

式中,k1,k2分别为一阶、二阶径向畸变参数,即相机标定的畸变参数,等待标定;ρ为畸变点到畸变中心C的像素距离.
2.3 双目视觉标定
图3为空间中任意点P在2个相机中的成像模型,点P1为点P理想成像点,点P2为P点发生畸变后的成像点(假设在光轴与像平面的交点上,实际是需要标定的点).图中的点P'为未进行畸变校正重建后的点,校正后重建点为真实点P.由图可以清楚地看到,DIC要进行三维匹配计算必须首先知道世界坐标系W与左、右相机坐标系CL,CR的转换关系,那么需要标定的相机外部参数有左相机的旋转矩阵RL和平移向量tL、右相机的旋转矩阵RR和平移向量tR、右相机相对左相机的旋转矩阵 RR,L和平移向量 tR,L.理论上固定相机后,RR,L,tR,L是固定值不变的.其次,标定左、右两个相机的内部参数AL,AR(等效焦距和图像中心),以及畸变参数 k1L,k2L,k1R,k2R.

图3 双相机成像模型
三维相机标定选取一些已知尺寸的参考物作为标定靶,常用的有原点、棋盘等图案.本文用2个相机拍摄若干张不同姿态的棋盘标定靶,利用非线性最小二乘优化方法L-M算法对2个相机的内部参数和相对位置参数做全局优化,这样可获得双目立体视觉系统的各个标定参数.
3 标定靶姿态数对标定稳定性的影响
在进行相机内部参数标定时,选择5幅图即可稳定[13];一般情况下,在外部参数标定时,尽量使棋盘绕横向、竖向、纵向旋转一定的角度,通常只需5组图.但在具体实验中,由于相机噪声的存在和环境因素的影响,若标定姿态过少则标定结果不够精确,标定姿态过多则不易于实验操作,尤其是在环境相对复杂的工程实验现场.本次实验所用相机为2048×2448像素,镜头焦距为50 mm.标定2个相机时,使用的图片数从5组姿态依次递增到13组姿态.如表1所示,随着标定姿态的增多,外参 RR,L和 tR,L标定逐步趋于稳定.
图4(a)~(c)分别为左相机的内部参数Cx,Fy,k1随标定姿态数变化值,结果显示,当标定板的姿态数大于9时,内参值变化相对稳定,此时相机内部参数标定的相对误差不超过2%,如图4(d)所示.因此,当标定板的有效姿态数达到9组以上,便可获得稳定可靠的相机标定结果,减少了过多标定姿态数给实验带来的麻烦.标定步骤的减少使得标定过程得到优化,为三维计算提供了保证.

表1 外参标定结果

图4 左相机内部参数稳定性分析
因此,让棋盘分别绕既定的三轴旋转一定的角度,获得9组以上的标定图片,即可获得稳定的标定结果.
4 应用实验
为了验证标定结果,可以测量一个已知试件的形貌.选择一个标准的圆弧型试件,拟合试件的半径,与真实值做比较.
选择半径为68 mm、宽度为40 mm的铝合金试件,使其沿离面方向产生刚体位移,选择标定板角点数为11×8,间距7 mm.计算模板选择29像素.处理实验结果,分别选择5组随意标定姿态图和10组优化的标定姿态图,通过三维DIC计算,由试件的三维形貌再拟合得出试件的半径.图5(a)为5组随意标定姿态图的拟合半径,拟合结果为68.8 mm;图5(b)是优化标定方案后的结果,半径为68.0 mm.

图5 优化标定前后拟合的试件半径
下面将运用较好的标定结果进行离面位移的计算.取一小区域的位移场计算平均值、最大值、最小值,并将结果与真实值比较,结果发现,二者的趋势一致,如图6(a)所示,所取区域各点位移的标准差平均值为0.001868 mm;图6(b)是对实际位移-1.0 ~-1.2 mm 的局部放大图.
5 结论

图6 离面位移与实际位移比较
本文从三维DIC的基本原理出发,分析相机的标定在对物体形貌和变形进行测量时有重要的意义.以标准板棋盘格作为参考物,分别考察了标定物的姿态对相机内、外参数等标定参数的影响.并且通过实验,对曲表面试件的半径和刚体位移进行考核.结果显示,要获得稳定的标定结果,只需要9组以上不同姿态的棋盘标定图,且不需要过多复杂的标定过程.优化标定后的结果可以使得三维DIC测量精度高于2 μm,证实了三维DIC不仅操作简便,还具有相当高的可靠性和精确度.
References)
[1]Peters W H,Ranson W F.Digital image techniques in experimental stress analysis[J].Optical Engineering,1982,21(3):427431.
[2]Sutton M A,Orteu J J,Schreier H W.Image correlation for shape,motion and deformation measurements:basic concepts,theory and applications[M].New York,USA:Springer,2009.
[3]Pan Bing,Qian Kemao,Xie Huimin,et al.Two-dimensional digital image correlation for in-plane dis-placement and strain measurement:a review[J].Measurement Scienceand Technology, 2009, 20(6):062001.
[4]Luo P F,Chao Y J,Sutton M A,et al.Accurate measurement of three-dimensional deformations in deformable and rigid bodies using computer vision[J].Experimental Mechanics,1993,33(2):123-132.
[5]伍小平.近40年光力学进展的回顾[J].实验力学,2010,25(5):491-508.Wu Xiaoping.A brief review of photomechanics progress in recent 40 years[J].Journal of Experimental Mechanics,2010,25(5):491-508.(in Chinese)
[6]施嘉伟,朱虹,吴智深,等.BFRP/HFRP布-混凝土界面黏结性能试验研究[J].东南大学学报:自然科学版,2010,40(3):554-558.Shi Jiawei,Zhu Hong,Wu Zhishen,et al.Experimental study on bond behavior between Basalt/Hybrid FRP sheets and concrete substrates[J].Journal of Southeast University:Nature Science Edition,2010,40(3):554-558.(in Chinese)
[7]Sun W,Quan C,Tay C J,et al.Global and local coordinates in digital image correlation[J].Applied Optics,2007,46(7):1050-1056.
[8]Chen F X,Chen X,Xie X,et al.Full-field 3D measurement using multi-camera digital image correlation system[J].Optics and Lasers in Engineering,2013,51(9):1044-1052.
[9]Lava P,van Paepegem W,Coppieters S,et al.Impact of lens distortions on strain measurements obtained with 2D digital image correlation[J].Optics and Lasers in Engineering,2013,51(2):576-584.
[10]Zhang D S,Luo M,Arola D D.Displacement/strain measurements using an optical microscope and digital image correlation[J].Optical Engineering,2006,45(3):0330605.
[11]Pan Bing,Yu Liping,Wu Dafang,et al.Systematic errors in two-dimensional digital image correlation due to lens distortion[J].Optics and Lasers in Engineering,2013,51(2):140-147.
[12]Fryer J G,Brown D C.Lens distortion for close-range photogrammetry[J].Photogrammetric Engineering and Remote Sensing,1986,52(1):51-58.
[13]Zhang Zhengyou.A flexible new technique for camera calibration[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2000,22(11):1330-1334.

