数学分析中极限概念的教学策略研究

孙业国

(淮南师范学院 数学与计算科学系，安徽 淮南 232038)

1 研究现状

国外关于极限概念的教学策略主要是运用四元素教学法(Four rules teaching methods)①路易斯·伏利德勒：《美国的微积分教学》，《高等数学研究》2005年第3期，第6－11页。。所谓四元素教学法是指每个数学概念都可以用图像、数值、符号、语言四种不同的形式展现给学生，从而使得学生能从不同的角度理解所学的数学概念。Howard Anton编著的微积分教材所采用的方法就是四元素法。教材中，作者首先对极限概念进行大量直观介绍，其次是讲述极限的求法，最后才阐述极限概念的精确定义。特别值得注意的是美国教材在讲解极限概念的时候，充分运用计算机进行教学，这样使得学生对极限概念有着直观的理解。然而，好的教学方法不能拘泥于某种特定的形式，要具体问题具体分析，这是我们教育工作者追求理想教育境界的不竭动力。

国内关于极限概念的教学方法主要是首先讲述极限的描述性定义，其次讲述极限的精确定义②谢太光：《再探数学分析教学难问题》，《西南师范大学学报》(自然科学版)，2005年第6期，第1142－1146页。－⑩陈惠勇：《数学史观下的数学概念教学新模式》，《高等数学研究》2007年第5期,第58－62页。。这种教学方法的关键在于如何让学生理解极限的描述性定义到极限的精确定义的过度过程。首先，运用实例导出极限的描述性定义，即随n的无限增大，an无限接近某个给定的常数a，我们称a是数列an的极限。其次，导出极限的精确定义：随着n无限的增大，an无限的接近某个常数a⇔随着n无限的增大，an和a的距离无限的减小⇔随着n无限的增大，|an－a|无限的减小⇔当 n充分大时，|an－a|可以无限小⇔当n充分大时，|an－a|可以小于任意给定的正数⇔∀ε〉0，当 n 充分大时，|an－a|〈ε，从而得出数列极限的精确定义：

2 极限概念教学难点分析

2.1 复杂的辨证思想

极限概念的定义，运用ε－N语言可以表述为：

极限定义蕴含二层意思，一是ε的任意性：定义中正数ε的作用是用来衡量数列an和给定常数a的接近程度。ε越小，表示an和a接近的越好。ε越大，表示an和a接近的越差。定义中的ε是任意给定的，因此ε可以任意的小，从而an和a可以任意的接近。然而，尽管ε是任意给定的，但是一旦给定，就会被暂时确定下来，运用这个确定的ε去寻找相应的正整数N。ε是任意小的正数，于是或者ε2等等也是任意小的正数，因此极限定义也可以表述为：

同时，ε是任意小的正数，于是可以限定ε小于某个确定的正数。而是N的相应性：一般情况下，N是随着ε的变小而变大，因此我们经常把N写成 N(ε)以表示N是和ε是有关系的。 然而，这并不意味着N是由ε唯一确定的。原因是对于任意给定的正数ε，假设当N=100时，能使得当n〉N时，有不等式|an－a|〈ε 成立，那么当 N=101 或者更大时，此不等式自然也成立。

2.2 抽象的数学语言

极限概念的描述性定义是很不精确的，无限接近只是一种定性的描述，无法运用数学的方法进行严格的推理论证，所以需要用精确的数学语言来定义极限。数列极限的精确定义是：

精确定义是一种逻辑结构严密且高度概括抽象的数学语言，给出了各变量的变化趋势，刻画了极限概念的本质。再例如函数极限的ε－δ语言

数学语言是一种数学思维和表达科学思想的载体。数学语言包括叙述语言、图形语言和符号语言，数学语言进行思维具有准确、简明、严密等特点。尽管数学语言具有准确、严密简明等特点，但由于其具有高度的抽象性使得在实践教学中成为教学的难点。

3 极限概念教学策略

3.1 数学史策略

数学史是研究数学学科发展和规律的一门学科，其主要内容是讲述数学思想和数学方法的演变过程。作为古老的数学概念，极限的朴素思想可以追溯到远古时代。我国庄子在《天下篇》中说：“一尺之棰，日取其半，万世不竭”，意思是说一尺长的棒子，第一天截取棒子的一半，第二天再截取剩下一半的一半，就这样无限的截取下去，随着天数的无限增加，棒子会越来越短，其长度越来越接近零，但是永远不会为零。上述截取的过程构成了一个等比数列{xn}

显然极限为零，即

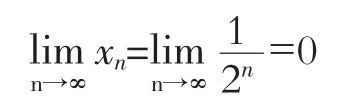
刘徽提出的割圆术“割之弥细，所失弥少，割之又割，以致不可割，则与圆合体而无所失矣”并运用其计算出圆周率π的近似值。假设圆的面积为S，圆的内接正 6×2n边形的面积为 Sn，显然 Sn〈S。随着对圆的分割次数的增加，圆的面积与正6×2n边形的面积之差S－Sn在减小，一直到圆不可以再分割时，内接正6×2n边形与圆重合，即

同时考虑到圆的面积公式为

于是运用可以得到圆周率 的近似值。通过上述例子我们可以看出，通过数学史的教学，让学生了解极限的来龙去脉，从而激起学生的学习兴趣。因此，对数学分析的教学无疑要考虑数学史实的运用。

3.2 数学思想策略

数学思想作为数学的重要内容，是铭记在人脑中起永恒作用的观点和精神，数学思想产生于人们在日常生活对数学的实践活动中，同时反过来对人们认识数学起着极其重要的指导作用，它能使人们懂得数学的价值，领悟数学的真谛，学会运用数学的思考和解决生活中的实际问题，是数学的精髓和灵魂。例如求极限的变量替换思想，考虑下面的例子

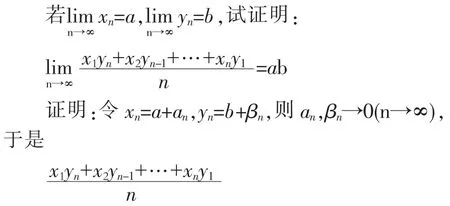
为了将未知的极限化简或转化为已知的极限，可以根据极限式的特点，适当引入新变量，以替换原有的变量，使原来的极限过程转化为新的极限过程，这就是我们所说的求极限的变量替换思想。通过上述例子，我们不难看出数学思想在数学教学中重要地位。因此，我们在数学概念教学时一定要应用数学思想策略。

3.3 数学实验策略

随着数学的不断发展和科技的不断进步，数学成为改变人们生活的重要工具，科技工作者对数学知识的需求也随之逐渐增强，以培养逻辑思维能力和计算能力为目标的传统数学课程已经远远不能满足现实的需要，新型复合型人才不仅需要传统意义上的逻辑思维能力和计算能力，更加需要数学建模能力、数据处理能力以及数值计算能力，数学实验课程就是为培养学生上述能力而特意设置的。我们在极限概念教学过程中，要适当运用数学实验策略培养学生的建模能力、数据处理能力以及数值计算能力，为把学生培养成适应社会的新型复合型人才奠定基础。

4 结论

教学没有确定的方法，同样也没有止境，以上讨论的是笔者结合平时教学总结出来的一些极限概念的教学方法，通过反复的实践，实践结果表明这些方法是可行的，在培养人才质量方面发挥积极的作用。然而，如何通过极限概念教学方法的改革从而更有效地培养创新型的人才，仍然是数学教育界所面临的一个极其重要的研究课题，为实现这一目标，我们还必须加倍努力，积极探索，不断实践。