生物细胞内不同类型钙振荡行为分岔研究

郑勇，平静水

（1.安徽工贸职业技术学院；2.淮南师范学院 数学与计算科学系，安徽 淮南 232001）

1 引言

钙离子（Ca2+）是生物细胞内重要的信使物质之一。研究发现，钙离子振荡可以控制细胞内很多重要的生理过程。描述钙振荡的数学模型不同于简单的电路系统，它具有多时间尺度，这也是生命科学中的重要现象。由于多尺度性，生物细胞才能呈现出比其他系统更复杂的振荡行为。如簇振荡是因为慢时间变量调节了快的峰振荡活动导致产生的静息态和连续峰振荡交替出现的振荡模式。因此，具有多个时间尺度的钙振荡模型能展现出复杂的非线性动力学行为。应用快慢动力学分岔分析①Izhikevich E.M.Dynamical Systems in Neuronscience:The Giometry of Excitability and Bursting.The MIT Press,2006.，即将慢时间变量作为分岔参数，研究快系统（快时间变量对应的系统）平衡点的分岔情况，既能解释簇振荡的产生机制，也能对不同模式进行分类。

在国际上 Borghans，Dupont，Goldbeter和 Shen基于产生复杂钙振荡行为的不同机理，如钙诱导的钙释放（CICR）和 IP3交叉偶联（ICC）机理，建立了4个模拟不同细胞类型钙振荡的数学模型。这些模型很好地模拟了胞内丰富的自由钙离子振荡模式，因此得到了广泛的研究②Goldbeter A.Biochemical oscillations and cellular rhythms.Cambridge:Cambridge University Press,1996.-④Grubelnk V.,Larsen A.Z.,Kummer U.and Olsen L.F.Mitochondria regulate the amplitude of simple and complex calcium oscillations.Biophys Chem,2001,94:59-74.。

2 模型

Borghans等学者基于钙触发钙振荡 (CICR)和钙刺激导致IP3浓度降低机理，对一类非兴奋型细胞进行了研究。在实验的基础上建立了能够模拟细胞内钙离子浓度振荡的数学模型，即Borghans-Dupont模型。Perc和Marhl等针对Borghans-Dupont模型⑤Perc M.and Marhl M.Different types of bursting calcium oscillations in non-excitable cells.Chaos,Solitons and Fractals,2003,18:759-773.，在外界刺激如荷尔蒙作为控制参数条件下，研究了细胞内多种钙簇振荡模式及混沌的产生和转迁机理。近年来，该模型中的同步、混沌控制等的研究也已展开①Shen P.,Larter R.Chaos in intracellular calcium oscillations in a new model for non-excitable cells.Cell Calcium,1995,17:225-232.-④Nchange,A.K.,Kepseu,W.D.and Woafo,P.Noise induced intercellular propagation of calcium waves.Physica A,2008,387:2519-2525.。

本文通过数值仿真发现了几种在文献中未涉及到的钙振荡模式，另外还可以模拟它们是如何随着系统参数的变化而变化的。生理实验与数学模型的数值仿真结合，才能研究各种离子通道对振荡模式的影响以及在内、外参数变化情况下的复杂非线性动力学行为，进而加深对Borghans-Dupont模型的理解。

其中，(1)式表示细胞液中钙浓度的变化；(2)式表示内质网中钙浓度的变化；(3)式表示IP3浓度的变化。Cacyt为胞液中的钙浓度，Caer为内质网(ER)中的钙浓度，IP3表示胞液中的IP3浓度。

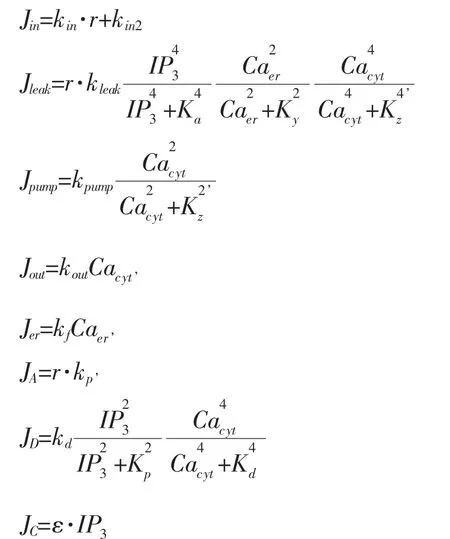
模型各参数值分别为：kleak=19.5 μM min-1，kpump=6.5 μM min-1，kin1=1 μM min-1，kin2=2 μM min-1，kp=2.5 μM min-1，kd=80 μM min-1，kf=1 min-1，kout=10 min-1，K2=0.1 μM，Ka=0.4 μM，KY=0.2 μM，Kz=0.3，Kp=1 μM，Kd=0.4 μM，ε=0.1。

3 结果

我们在参数r的合理范围内，通过改变它的值来研究模型出现的钙振荡行为。选取Caer为慢变量，讨论模型中可能出现的钙振荡模式。当参数r=1时，细胞内钙浓度呈现图1所示的拟周期簇振荡模式。这种簇振荡的产生机制是由于全系统遇到了一个超临界Neimark-Sacker分岔，它的特征是第一和第二李雅普诺夫指数均为零。从图1（b）中，可以看到在它的相空间内存在一个环面（torus）。当r继续增加时，这个环面吸引子在r=1.0073时，会遇到一个具有同宿环面结构的极限环鞍结分岔而变为周期的簇振荡行为。当参数r增加至1.05时，系统呈现一种不同形式的钙振荡模式，如图2所示。随着系统参数r的增加，细胞钙振荡由前面的拟周期簇振荡变为周期簇振荡。用图2（b）的分岔分析，可研究此种类型簇振荡的动力学性质及其类型。

图1 r=1时，系统引起的拟周期簇振荡

图2 r=1.05时，系统引起的点-环型“subHopf/subHopf”簇振荡

如图 2（b），据仿真结果，快子系统（1）与（3）的平衡点就其分岔参数（即慢变量Caer）的不同的值，在(Caer，Cacyt)相平面上形成一条S形分岔曲线，将图2（a）的簇振荡轨线也叠加在图中。可以看出，快子系统关于Caer形成的S形曲线由三部分组成：上支、中支和下支。在S形曲线的上支部分，平衡点都是稳定的焦点，随着Caer的减小，稳定的焦点经过亚临界Hopf分岔点sub H失稳，变为不稳定的焦点。中支是由不稳定的鞍点组成，其上存在一个满足条件 λ1+λ2=0的中立鞍点， 其中 λ1，λ2是快变子系统的Jacobi矩阵的特征值。在S形曲线的下支部分，平衡点都是稳定的结点。

经亚临界Hopf分岔点sub H产生的不稳定的极限环在LPC点发生极限环的鞍结分岔，此时稳定的极限环和不稳定的极限环合并且消失。从图2（b），可以看出点LP1处的鞍结分岔是远离极限环的鞍结分岔。

随着参数Caer的减小，稳定焦点组成的上状态经亚临界Hopf分岔消失，转迁到下支的稳定结点。反之，参数的增加可使下状态经亚临界Hopf分岔消失而转迁到上状态。为了更好地解释这种点-环型“Hopf/Hopf”簇振荡，我们以图 2（b）中逆时针方向来跟踪全系统的轨线。轨线沿着S形曲线的下支快速移动经由鞍结分岔LP1跃升到S形曲线上支的稳定焦点上，之后由于稳定极限环的吸引性，轨线围绕着S形曲线的上支作振幅逐渐衰减的运动，最终轨线收敛到S形曲线的上支的稳定焦点。因此，当参数r=1.05时，该模型的簇振荡模式表现出点-环型“subHopf/subHopf”簇振荡的动力学性质。

当参数r继续增加时，快变子系统关于慢变参数Caer的分岔结构发生了变化。r=1.16时，（Caer，Cacyt）平面上的分岔图，如图3。与r=1.05的情形相比，少了极限环的鞍结分岔LPC，多了一个同宿轨分岔homo。

与图2相比，图3中的快变子系统关于慢变参数Caer的分岔结构非常类似，事实上它们对应的钙振荡类型是不同的。我们运用图3（b）的快慢动力学分岔分析，来研究此簇振荡的动力学性质及其类型。

如图3（b），根据数值计算结果，快变子系统（1）与（3）的平衡点就其分岔参数（即慢变量Caer）的不同的值，形成了在(Caer，Cacyt)相平面上的一条S形分岔曲线，并且将图3（a）的簇振荡轨线附加于图中。从图中可以看出，快变子系统关于Caer形成的S形曲线由三部分组成：上支、中支和下支。在S形曲线的上支部分，平衡点都是稳定的焦点，随着Caer的减小，稳定的焦点经过亚临界Hopf分岔点sub H失稳，变为不稳定的焦点。中支是由不稳定的鞍点组成，其上存在一个满足条件λ1+λ2=0的中立鞍点，其中λ1，λ2是快变子系统的Jacobi矩阵的特征值。在S形曲线的下支部分，平衡点都是稳定的结点。

图3 r=1.16时，系统引起的点-点型“subHopf/subHopf”簇振荡

与图2不同之处在于，r=1.16时，经亚临界Hopf分岔点sub H产生的不稳定的极限环并未发生极限环的鞍结分岔，也就是说系统此时只有不稳定的极限环，而没有稳定的极限环产生。

当分岔参数Caer减小时，稳定焦点组成的上状态经亚临界Hopf分岔（sub H）消失，变为由稳定结点构成的下状态。随着Caer的增加，下状态经亚临界Hopf分岔（sub H）消失而转迁到上状态。为了更好地解释这种点-环型“Hopf/Hopf”簇振荡，我们以图3（b）中逆时针方向来跟踪全系统的轨线。轨线沿着S形曲线的下支快速移动经由鞍结分岔LP1跃升到S形曲线上支的稳定焦点上，之后由于稳定焦点的吸引性，轨线围绕着S形曲线的上支作振幅逐渐衰减的运动，最终轨线收敛到S形曲线的上支的稳定焦点。因此，当参数r=1.16时，该模型的簇振荡模式表现出点-点型“subHopf/subHopf”簇振荡的动力学性质。

极限环的同宿轨分岔对簇振荡的类型并不产生影响，但却十分重要。它阻止了不稳定极限环变为稳定极限环，因此这种簇振荡类型属于点-点型“subHopf/subHopf”簇振荡而不是图2的点-环型“subHopf/subHopf”簇振荡。

事实上，从图2和图3我们还可以观察到一个重要现象，即所谓的慢通道效应（slow passage）。在轨线沿逆时针方向穿过亚临界Hopf分岔点之前，系统非常靠近静息态，当轨线慢慢地穿过分岔点时，系统依然很靠近静息态，但此时稳定状态已经变得不稳定。之后，轨线从不稳定焦点开始发散并逐渐向S形曲线的下支的稳定结点方向展开。轨线在S形曲线的不稳定上支附近持续振荡了一段时间后才发散并回到S形曲线的稳定下支。

当参数r继续增加时，如r=1.193，此时系统将呈现简单的峰振荡模式。上述的慢通道效应也随即消失。

4 结论

本文就具有快慢时间尺度的两类不同触发机理的钙振荡数学模型，利用非线性分岔分析和快慢动力学分析，对其振荡区域和振荡类型进行了详细的研究。在振荡区域发现了多种振荡模式，如周期性簇振荡、拟周期性簇振荡及峰振荡。除了增加突触传递的可靠性之外，簇振荡还可以为细胞之间的选择性的信息传递提供有效的机理。

对于描述一类非兴奋型细胞，特别是上皮细胞和肝细胞内钙振荡的Borghans-Dupont模型，讨论了不同强度的外界刺激（如荷尔蒙）条件下，系统呈现的三种不同类型的复杂钙振荡类型。虽然这些钙振荡所属类型不同，但相应的快变子系统的分岔参数曲线是类似的，均为S形分岔曲线。

当r=1时，细胞内钙离子浓度呈现拟周期簇振荡模式。指出这种簇振荡的产生机制是由于全系统遇到了一个超临界Neimark-Sacker分岔。当r继续增加时，这个环面吸引子在r=1.0073时，会遇到一个具有同宿环面结构的极限环鞍结分岔而变为周期的簇振荡行为。

当r=1.05时，细胞内钙离子浓度呈现点-环型“subHopf/subHopf”周期性簇振荡模式。

当r=1.16时，细胞内钙离子浓度呈现点-点型“subHopf/subHopf”周期性簇振荡模式。

点-点型“subHopf/subHopf”周期性簇振荡模式中存在一个极限环的同宿轨分岔，它对簇振荡的类型并不产生影响，但却十分重要。它阻止了不稳定极限环变为稳定极限环，因此这种簇振荡类型属于点-点型“subHopf/subHopf”簇振荡而不是点-环型“subHopf/subHopf”簇振荡。

当参数r继续增加时，如r=1.193，系统将呈现简单的峰振荡模式。

就生物细胞系统而言，本文主要做了基于单参数变化的相关研究，尚未涉及到多参数的情形。实际上，只有当多个参数同时变化时才更符合实际，因此高余维分岔行为有待进一步研究。