静子结构振动分析中叶片的有限元建模方法研究

孙阳，王克明，张婷婷，李想

（沈阳航空航天大学航空航天工程学部，沈阳 110136）

1 引言

叶片是航空发动机中最重要的零件之一，本文针对某型航空发动机典型的静子结构，以分析周向弯曲振动模态频率为目的，对机匣、一圈叶片、加强内环组成的静子结构研究其叶片的有限元模型的简化方法。真实的叶片模型结构复杂，建立有限元模型是一件繁琐复杂的工作，考虑航空发动机中叶片数目庞大和叶片的有限元模型简化对多级静子结构或整机振动的影响，权衡计算精度和计算规模，对这种典型结构中叶片的简化建模方法研究是非常有意义的。

2 带内环静子结构的有限元模型

选取某型航空发动机压气机部分某级静子结构中垂直于发动机中轴线的一个截段为研究对象，该截段中包含了静子系统中的典型结构机匣、一圈静子叶片、内环。考虑内环在同等质量下的周向抗弯刚度，横截面设计为工字型；全部叶片圆周对称的分布在机匣与内环之间，连接了机匣和内环。应用UG建模软件建立结构模型如图1。

图1 带内环静子结构的几何模型

2.1 结构的有限元模型

由于叶片结构有其特殊性，有进气边和放气边的存在，选择四面体网格划分，单元类型选用带有中间节点的10 节点SOLID186 单元。应用ANSA 软件划分网格后有限元模型单元数量为487766个，有限元模型的局部细节如图2所示。为了得到较为单纯的周向弯曲振型，在选取短截段的同时需在机匣截段的一个截面施加延发动机中轴线方向的位移约束，这样通过有限元软件分析得到的振型为单纯的周向弯曲振型。

图2 带内环静子结构的有限元模型局部

2.2 模态分析结果

将有限元模型导入ANSYS 软件中进行模态分析，模型参数选择如下：弹性模量E＝210000N/mm2；密度ρ＝7.85×10-9t/mm3；泊松比μ=0.3。计算得前10阶周向弯曲模态频率如表1 中所示，对应的前6阶振型如图3。

图3 结构的周向弯曲模态振型

3 有限元模型的简化

叶片的弯曲在气体动力学分析中是不可忽略的，但是在结构的振动分析中主要考虑结构的弹性和惯性。叶片建立模型和划分网格是一件复杂的工作，采用矩形截面的梁代替叶片，等效叶片的弹性和惯性建立有限元模型，模型变得简单的同时有限元的计算规模明显减小。

图4 结构中静子叶片的模型

3.1 用矩形截面梁等效叶片的简化

模态分析中主要考虑结构的弹性和惯性，对叶片进行简化建立有限元模型，简化前后应有等效的刚度和质量。真实的叶片模型通过叶片展向由上至下的6个截面扫略而成，如图4，考虑采用等效截面性质的方法，将6个叶形截面分别用等效的矩形截面代替。

观察图3的振型，叶片主要以拉压和弯曲变形为主，简化后的结构应有与其对应弹性变形的抗变形刚度，具体方案如下：

（1）每个对应截面的面积相等，这样通过6个截面成型的结构有等效的质量和惯性，由结构的抗拉压刚度K＝EA（A为截面面积）可知，简化前后的拉伸和压缩的刚度相等；

（2）简化前后的抗弯刚度相等，结构的抗弯刚度K＝EI（I 为截面到其中性轴的惯性矩）［4］，弹性模量E 不变，简化前后应有相等的惯性矩I′＝I。

图5 叶片的叶形截面

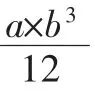
得到与1 截面等效的矩形截面，其它5个截面采用同样方法依次计算。这样的考虑基于理想状态之下，结构的弯曲为平面纯弯曲且忽略了拉压和弯曲的刚度叠加效果。最终得到6个矩形截面尺寸分别为：

图6 与静子叶片等效的梁模型

通过6个矩形截面建立与叶片等效的梁模型如图6。

3.2 计算结果对比

简化后的结构的有限元模型局部细节如图7，规整的模型可采用六面体网格划分有限元模型。单元数量为27824个，与简化前（487766个）相比，计算规模大为减小。计算结构前10阶周向弯曲振动的模态频率与保持叶形结构的对比如表1，由表1 可知，采用六面体网格划分，用较少的单元数量即可得到吻合较好的计算结果。

4 结论

图7 简化后的六面体网格的局部模型

表1 简化前后结构的模态频率对比

用有限元法对带有内环的典型静子结构进行周向弯曲模态分析时，可以采用等效截面的刚度和惯性的方法，将形状复杂的叶片简化为矩形截面梁。简化后的模型简单规整，可划分高质量的六面体网格，模态分析的计算结果有很好的吻合，计算规模大为减小。

［1］金基铎，王克明.机械振动基础［M］.沈阳：沈阳航空工业学院，2001.

［2］刘长福，邓明.航空发动机结构分析［M］.西安：西北工业大学出版社，2007.

［3］张利民，王克明，吴志广.叶片模态的分析单元类型选择［J］.沈阳航空航天大学学报，2011，28（4）：21-24.

［4］刘鸿文，林建兴，曹曼玲，等.材料力学［M］.北京：高等教育出版社，2004.

［5］冷纪桐，赵军，张娅，等.有限元技术基础［M］.北京：化学工业出版社，2007.

［6］送玉泉，管志平，聂毓琴，等.圆管的刚度和强度分析［J］.中国科学E 辑（技术科学），2006，36（11）：1263-1272.

［7］徐芝纶.弹性力学［M］.北京：高等教育出版社，2006.

［8］吴志广，王克明，张利民.静子叶片内环结构对机匣动力特性的影响［J］.沈阳航空工业学院学报，2010，27（4）：23-26.

［9］王宏祥，王红静，何勍.一类轴对称圆环的弯曲振动分析［J］.辽宁工学院学报，2004，24（2）：30-31.