小导管注浆粘土隧道破坏机制的试验与理论研究

许 明，刘先珊

（重庆大学 土木工程学院，重庆400045）

超前预支护是具有开放工作面的软土隧道掘进施工过程中一种常见的工艺方法，是在隧道开挖之前，在掌子面前方的地层里，沿隧道横断面设置一个类似伞形拱壳的连续体或加固体，用以加固掌子面前方的地层，保证掌子面及地层的稳定，抑制地表的沉降，形成一个超前的支护体系。在实际工程中，虽然已经形成隧道小导管超前注浆的参数设计、施工工艺标准、质量管理和计量控制等相关的标准［1－2］，但主要基于经验类比模式。小导管注浆的加固机理一般均简化为梁拱效应和地层加固效应［3－6］；加固效果的评价多采用环状加固区力学参数反演基础上的数值计算方法［7－8］。而小导管注浆对于地表沉降和隧道塌陷机制的效应尚缺乏完善的理论分析和验证。

本文运用伦敦城市大学Acutronic 661型离心机研究超前小导管注浆加固圆形隧道的塑性变形机制，分析超前小导管作用机理以及小导管注浆“拱顶加固”工艺对隧道稳定性的影响。在此基础上，从塑性极限分析上限法的基本原理出发，构建小导管注浆粘土隧道的垮落机制。Davis EH曾给出单隧道4种上限垮落机制，其中机制D是顶部、两邦和底部垮落模式，有3个变量角［9］，但该机制主要模拟无支护的圆形隧道，而隧道中的支护结构将显著改变软土隧道的破坏模式。本文依据离心模型试验中“拱顶加固”隧道的变形垮落形迹，重新拟定塑性滑移面位置，采用解析法推导稳定率上限方程，通过该方程进一步讨论隧道埋深、土体强度及小导管注浆体对单圆形隧道稳定率上限解的影响。最后，由离心模型试验结果证实其上限解的正确性。

1 离心模型试验

1.1 隧道模型

试验模型由搅拌均匀的Speswhite高岭土（Gs＝2.62，wL＝65%，wP＝35%，φ′＝23°）泥水浆在一个硬铝箱中排水固结制备而成，初始含水量w＝120%。铝箱内径为550mm×200mm×375mm，底部加工有连通的V型排水槽。竖向有效固结压力σ′v逐级增加并维持在350kPa，历时8d，成型后试件标高207mm，质量128.5kg。铝箱旁固定有一空心立柱，内有溢水管，液面保持与试件等高。

隧道埋深C与隧道直径D之比取为2。隧道直径为50mm，离心机回转半径为1.8m，加速度设为100g（235rpm），根据相似原理，试件可模拟5m直径的隧道，该尺寸是城市地下铁路开挖中常用的建筑限界。隧道拱脚距离试件模具箱底一倍直径以上，两侧距离箱体5倍直径。其他类似尺寸的离心机试验结果表明，隧道拱脚附近的位移较小，该距离可以将边界条件对实验结果之影响减至最低。

在隧道开挖阶段，用空心圆柱状夹具固定一个外径50mm的薄壁不锈钢管，事先润滑，精确校位，将其推入试验隧道位置处，贯穿试件的整个宽度，小心拔出即可开凿出试验所需的隧道。隧道内壁用厚度0.75mm的柱状密闭橡胶膜覆盖，试验过程中通过压缩空气对隧道内壁施加支撑抗力。

为测量模型的地表以下位移，须在试件侧面布置观测点，每个观测点由一个直径3mm的黑色圆柱状塑料钉镶嵌在试件表面标记，如图1（a）所示。

1.2 注浆小导管

试件采用拱顶加固方案，注浆小导管加固区采用φ5的不锈钢管钻孔后，浇筑可固化的合成树脂（Biresin G27，Sylmasta Ltd）进行模拟［10］。液态树脂在一定注浆压力作用下，4min完成沉积固结，贯穿试件整个宽度（隧道轴向）方向，相互重叠形成环状加固区。环状拱壳布置在隧道拱顶180°范围内（共25根，图1（b）），密度ρ＝1 563.2kg／m3，弹性模量E＝2 535MPa，距离隧道开挖轮廓线δ＝5mm，其厚度为浆液扩散半径（R＝2.5mm）的两倍。注浆管中心距离隧道轴心32.5mm，相邻导管环向间距S＝4.25mm，环向圆心角θ＝7.5°。注浆区的主要尺寸如图1所示。

图1 试件模型布局图

为考察小导管注浆工艺对地表沉降和隧道稳定性的影响，试验还进行了无支护隧道的塑性变形机制研究，作为参照及比较。试验关键之处在于确保试件处于二维平面应变条件下考察隧道内壁所需的支撑应力与土体变形的关系。由于地表沉降与隧道轴向正交［11］，这种简化尽管忽略了花管的倾角，但由于隧道的变形集中在与隧道轴向垂直的平面内，除了不能模拟隧道掌子面的破坏以外，是一种有效的近似。

1.3 试验流程

在离心机加速阶段，隧道内的压缩空气压力也逐渐增加，以平衡不断增大的拱顶上覆压力，最终的气压设定为210kPa，约等于隧道轴线处的地压，土体开始二次固结。在偏离隧道中线横向间距155mm处预埋有3个不同高程的DruckPDCR81微型孔隙水压力计，待24h后，孔隙水压力趋于稳定，试件达到新的应力平衡后即可开始试验。隧道的开挖过程通过减小其内部充盈的空气压力进行模拟，速率约为每分钟减小100kPa，隧道将发生显著变形并坍塌。试件地表沉降采用12个间距45mm的线性位移传感器（LVDTs）进行测量，地下位移则通过图形采样分析系统（Visimet）对不同时刻观测点几何位置的分析来获取相应点的位移［12－15］，采样频率为1Hz／s。试验结束后，用十字板剪切仪测得隧道轴心深度处土体不排水剪切强度为40kPa左右。

2 试验结果分析

2.1 地表沉降

图2（a）为无支护隧道横向地表沉降槽曲线，横轴表示偏离隧道轴线的水平距离，5条曲线分别对应地层损失率为2%、5%、10%、15% 和20%时地表沉降，可见，横向地表沉降槽符合高斯曲线特征，地表最大沉降位于隧道中心线处，其表达式为［16］：

式中：Sv为横向地表沉降；Smax为隧道中心线处地表最大沉降量；x为偏离隧道中线的横向距离；i为地表沉降槽宽度系数，是自隧道中心至沉降曲线反弯点的距离。

有支护隧道的地表沉降槽曲线如图2（b）所示，在相同的地层损失率情况下，最大地表沉降仅下降了1%～2%，i值几乎保持不变。注浆导管的存在与否对沉降曲线影响甚微。

2.2 隧道的稳定系数

在隧道的模拟开挖阶段，隧道内壁支撑应力σT随地层损失率VL（单位距离内沉降槽体积占隧道开挖体积的百分比）的变化情况示于图3中。实际工程中地层损失率通常在1%～2%范围内，但试验中σT持续减小至隧道完全失效，VL可达到较大的数值。隧道失效时的临界支撑应力可通过σTVL曲线的渐近线进行估值，无支护隧道σTC1＝40.9kPa，有支护隧道σTC2＝13.5kPa。相同的支撑应力条件下，无支护试件的地层损失率较大；相同的地层损失率条件下，无支护试件所需的支撑应力较大，特别是隧道发生大变形时更为显著。

图2 横向地表沉降槽曲线

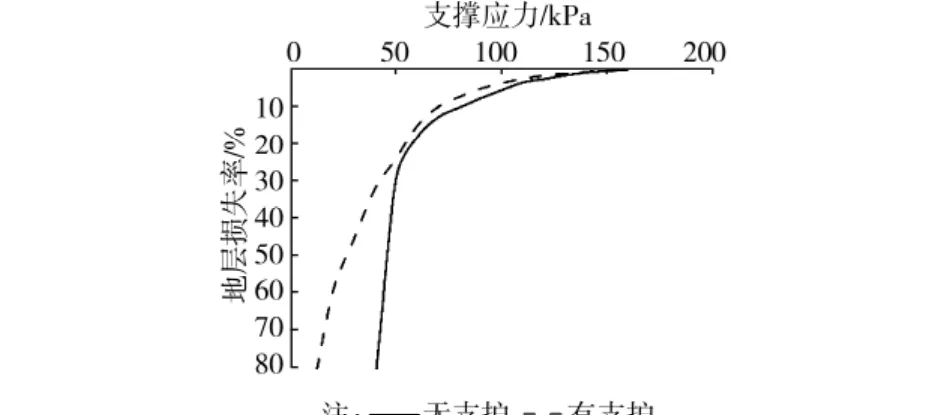
图3 支撑应力与地层损失率的关系

为了衡量隧道的稳定状况，许多学者［17］提出用稳定率N（或称稳定系数）作为评价隧道稳定状况的指标，其表达式为：

式中：σs为隧道上方地表分布压力；γ为土的容重；z0为隧道轴线埋深，z0＝C＋D／2；σT为隧道内支撑应力；Su为隧道轴心深度处土体不排水剪切强度。

相同条件下，隧道所需的临界支撑应力越大，稳定率N越小，隧道越不稳定。无支护隧道所需的支撑应力大于有支护隧道，由此可见，隧道轮廓线外围的注浆导管对隧道拱顶能提供一定的支撑，进而提高隧道稳定性。

3 极限分析的上限解

极限分析上限法基本原理认为，在一个假设的，且满足速度边界条件及应变与速度相容条件的速度场中，由外功率等于所消耗的内能而得到的荷载不会小于实际破坏荷载。若隧道垮落机制（模型）被确定，据隧道周边的刚性块体机动容许速度场建立功能方程，求得稳定率表达式，从变化角度找到稳定率最优值（最小上限值）［18］。一旦某隧道稳定率达到此值时，表明此隧道已垮落。在求解稳定率上限解中，为简化计算，假设隧道周边的速度场由理想刚塑性材料组成，不可压缩，土体湿剪切强度Su为定值。

图4给出了VL＝20%时离心机试验的位移场分布，据此拟定上限垮落机制的计算模型，隧道周边的速度场及不连续面的假定如图5所示。块体速度矢量指向隧道中线上偏离隧道轴线一定距离的某点。由于小导管注浆体的刚度远大于土体，块体之间的塑形滑移面不允许从小导管注浆区穿过。

图4 位移场

在图5中，圆形隧道周边的速度场由5个刚性块体组成，块体之间由厚度为0的速度不连续面相连接。地表垮落宽度2B由隧道直径D、赋存深度C、土的容重γ、湿剪切强度Su、隧道上方地表分布压力σs和隧道内支撑应力σT等因素决定。隧道两侧的滑移角α、θ、2β将随上述影响因素而变化。此垮落机制为中心对称，因此，图5左半部被用于图6所示的计算模型。

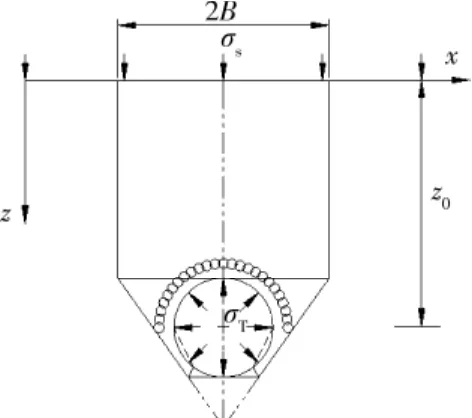
图5 计算模型

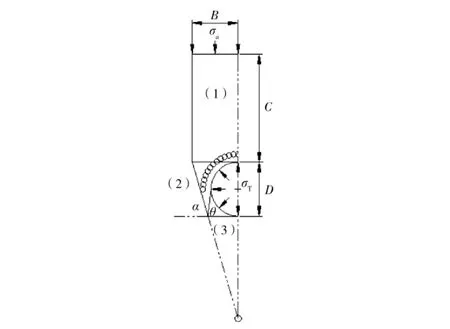
图6 左半部模型

该模型由块体（1）、（2）和（3）组成，图7为块体速度场和外力分布图，块体速度分别为V1、V2、V3，块体间的相对速度为VEA、VNF。块体（2）左边界与小导管注浆区相切，速度矢量V2指向隧道中线上的O点；块体（3）下边界与拱脚平齐，块体（2）与块体（3）交于NF线；隧道轴心为J点，令∠MJN＝2β，OM＝x。由于作用在滑移面上的正应力不做功，所以不予考虑。

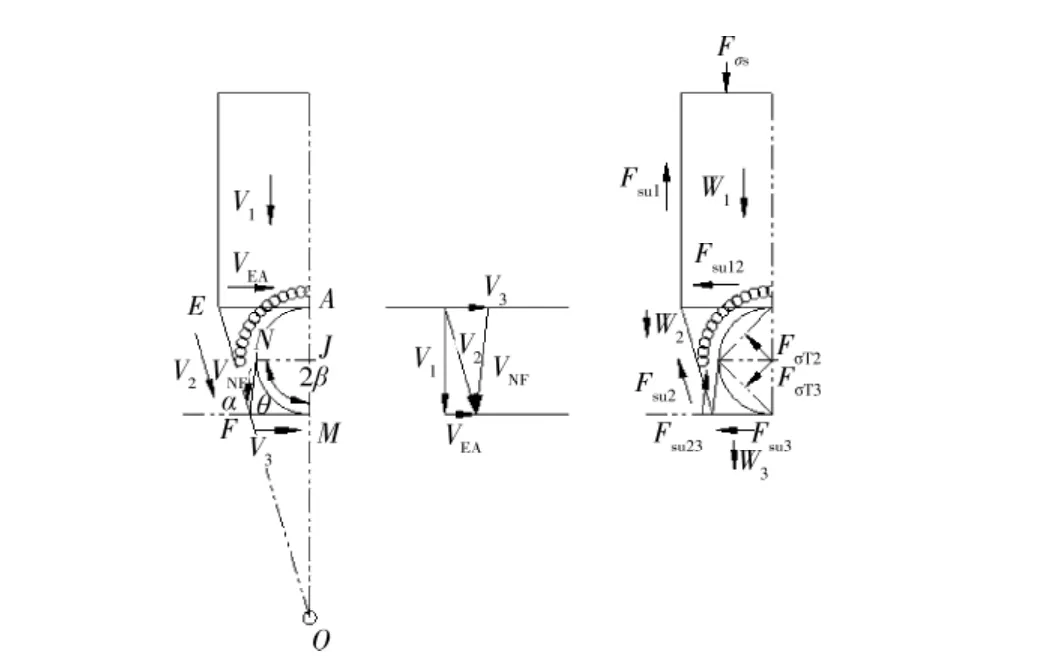
图7 块体速度场和外力分布图

由几何关系，滑移面长度EA、EF、FM、NF分别为

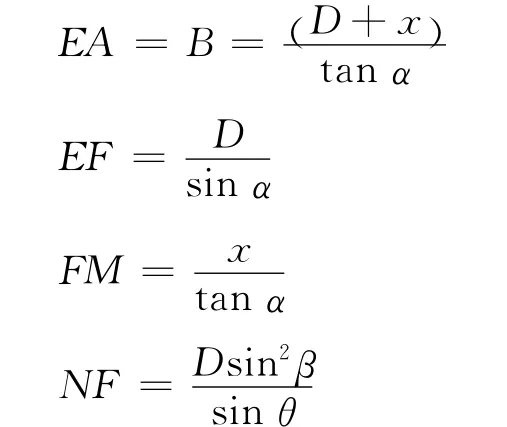
设块体（1）的下降速度V1＝V，则其余速度可表示为

图7中，W1、W2、W3为块体所受的重力；Fσs、FσT2、FσT3为σs、σT作用于地表及隧道周边的合力；FSu1、FSu2、FSu3、FSu12、FSu23为作用于滑移面上的剪切力，以阻止块体运动。这些力可表示为：

由假设可知，块体为刚体，块体内土的变形能为0，则外力所做的功W和滑移面所耗内能E可分别表示为

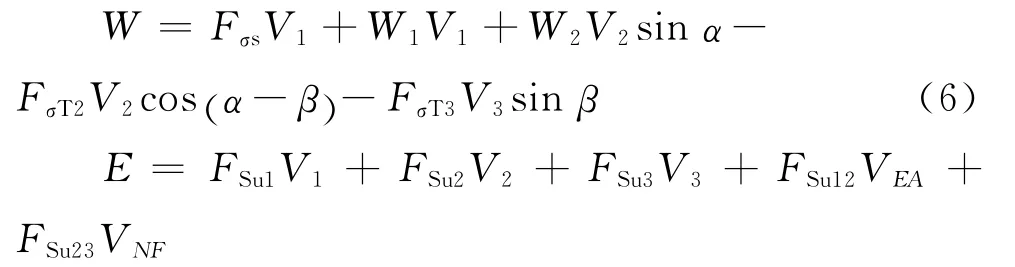
据功能原理W＝E，有

将x带入式（7），有

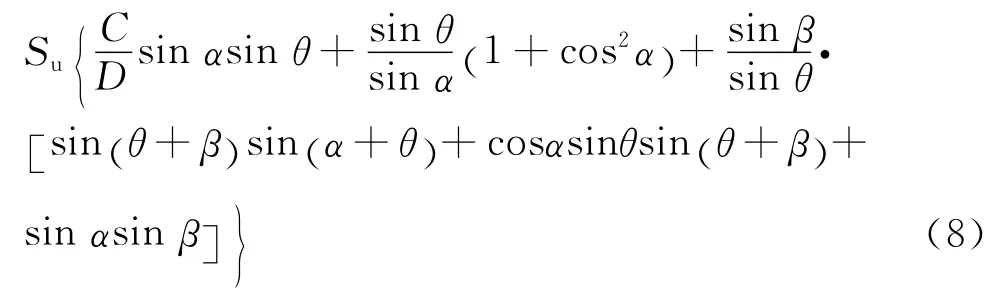
以稳定率N表示式（8），即可得到无支护隧道稳定率上限方程，要获得最小稳定率上限，可采用解析法或数值计算求最优值（极小值）。

3.1 埋深（C／D）的影响

通过求解式（8），在σs＝0，D＝5m，γ＝17.5 kN／m3，su＝40kPa条件下，临界稳定率Nc与覆跨比C／D的关系见表1。

表1 不同埋深时的临界支撑应力和稳定率

当隧道稳定率达到临界值时，刚性块体的边界如图8所示，图中数值代表不同覆跨比时对应的边界位置。随着隧道埋深的增加，隧道失稳时周边滑动块体的面积增大，洞壁的变形区域减小，维持隧道稳定所需的内支撑应力随之增加，块体（2）速度矢量交点由拱脚以下某点逐渐向拱脚靠拢。

对于离心机试验中无支护隧道，覆跨比C／D＝2，隧道失效时的临界支撑应力σT＝44.80kPa，α＝56.1°，θ＝57.3°，β＝46.0°，与通过σTVL曲线的渐近线获得的临界支撑应力接近（无支护隧道σTC1＝40.9kPa）。临界稳定率Nc＝4.3，与其他学者获得的平面应变圆形隧道塑性极限分析的上限解一致；土体位移矢量指向隧道中线上距离隧道轴线1.74D的一点，与图4（a）位移场观测结果一致。

图8 隧道垮落时的块体边界

无支护隧道的破坏机制及失稳图像如图9所示，洞壁变形区域集中在隧道轴线以上高程，塑性极限分析的上限法与试验结果一致。

图9 无支护隧道失稳图像

3.2 土体强度 （γD／Su）的影响

在σs＝0，C／D＝2，D＝5m，γ＝17.5kN／m3条件下，临界稳定率Nc与γD／Su的关系见表2（su分别等于87.50、43.75、29.17、21.88kPa）。

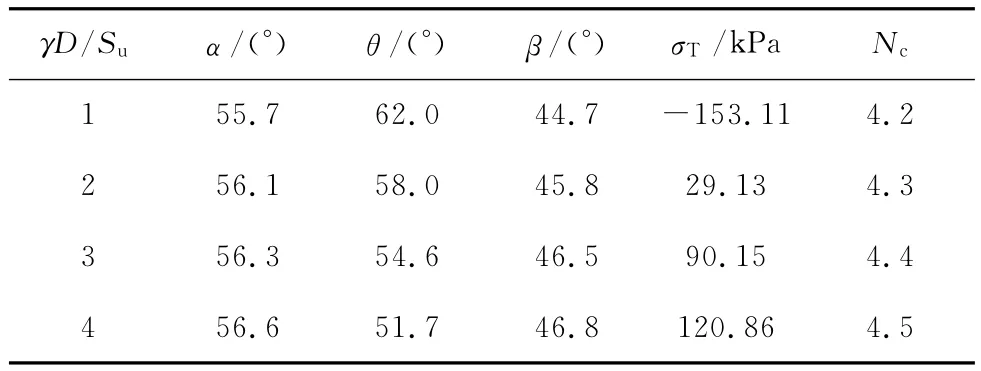
表2 不同强度时的临界支撑应力和稳定率

当隧道稳定率达到临界值时，刚性块体的边界如图10所示，图中数值代表不同土体强度时对应的边界位置。随着土体不排水剪切强度的降低，隧道失稳时周边滑动块体的面积略有增大，洞壁的变形区域及块体速度矢量交点几乎保持不变，仅维持隧道稳定所需的内支撑应力增大。可见，相同埋深条件下，土体强度对隧道失稳模式的影响较小。

3.3 小导管注浆区的影响

对于隧道有支护的试件而言，σs＝0，C／D＝2，γ＝17.5kN／m3，D＝5m，su＝40kPa，隧道失效时的临界支撑应力σT＝18.43kPa，α＝54.6°，θ＝60.8°，β＝18.4°，与通过σTVL曲线的渐近线获得的临界支撑应力接近（有支护隧道σTC2＝13.5 kPa）。与无支护隧道比较，滑移角α、θ变化不大，但隧道开挖轮廓线外布置的密排注浆管，将显著改变地层剪应力的分布，使滑移面EF向注浆区移动，σT及β显著减小，洞壁破坏轮廓线从块体（2）的隧道轴线以上高程向轴线以下高程转移，并逐渐向拱脚集中（图11（a），虚线为隧道失稳时的洞壁轮廓线）。土体位移矢量指向隧道中线上距离隧道轴线D的一点，与图4（b）位移场观测结果一致。

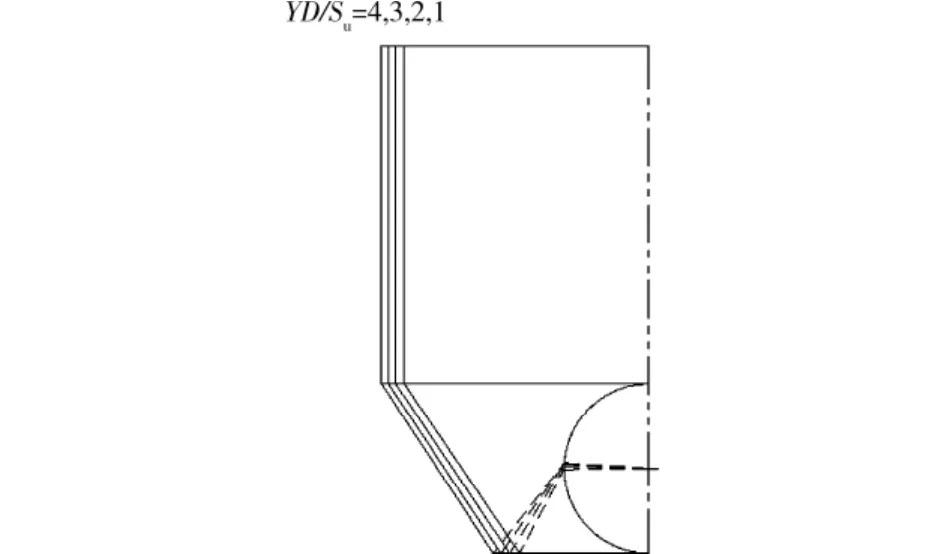
图10 隧道垮落时的块体边界

图11 有支护隧道失稳图像

4 结 论

1）采用离心机模型试验对粘土隧道超前导管注浆的加固机理与地层运动机制进行研究，注浆导管改变了隧道外围的边界条件和剪应力分布，能对隧道拱顶提供一定的支撑，隧道塑性区由拱顶向拱脚转移，深部土体逐渐开始参与承载，滑移面向注浆区移动，并逐渐向拱脚集中，隧道稳定性得以提高。

2）注浆导管的存在与否对地表沉降及沉降槽形状影响甚微，土体位移矢量近似指向隧道中线上拱脚以下某一点，注浆导管的布置方式决定着该点与隧道轴线的距离，原因在于土体水平位移分量与竖直位移分量之比较之参照试验发生了改变。

3）通过对单个圆形隧道稳定率上限方程的分析，建立了小导管注浆圆形隧道的垮落机制，得出了稳定率上限解。在σs＝0，C／D＝2，D＝5m，γ＝17.5kN／m3，su＝40kPa条件下，求得的稳定率上限解与离心机试验结果一致，所建立的破坏机制也与隧道失稳图像吻合。

（致谢 伦敦城市大学R.N.Taylor教授在圆形隧道稳定性分析方面给予第一作者悉心指导，在此表示衷心感谢！）

［1］重庆交通科研设计院.JTG D70—2004公路隧道设计规范［S］.北京：人民交通出版社，2004：214－>215.

［2］张凤爱.浅谈对隧道超前小导管注浆的质量管理［J］.公路交通科技：应用技术版，2011，7（8）：292－>294.Zhang F A.Elementary talkabout quality administration on thEtunnel per－>forEpouring liquid with small pipe［J］.Journal of Highway and Transportation Research and Development：Application Technology Edition，2011，7（8）：292－>294.

［3］周兴国，高永涛，卢宏建，等.超前注浆小导管支护机理与效果分析［J］.西安建筑科技大学学报：自然科学版，2010，42（4）：545－>549.Zhou X G，Gao Y T，Lu H J，et al.Study of supportmechanism and effect of advancEgrouting ductilEtechnology ［J］.Journal of Xi'an University of ArchitecturE＆ Technology：Natural SciencEEdition，2010，42（4）：545－>549.

［4］王铁男，郝哲，杨青潮.超前小导管注浆布置范围对地铁隧道开挖的影响分析［J］.公路，2011，40（5）：222－>227.Wang T N，Hao Z，Yang Q C.Analysis of influencEof advancEsmall duct pre－>grouting layout onmetro tunnel excavation［J］.Highway，2011，40（5）：222－>227.

［5］许宏发，江淼，王发军.变径洞室超前支护开挖模拟与分析［J］.岩土力学，2010，31（Sup1）：376－>382.Xu H F，Jiangm，Wang F J.Simulation and analysis of excavation of variablEcross－>section cavern with advanced support［J］.Rockand Soilmechanics，2010，31（Sup1）：376－>382.

［6］练志勇.突变大断面地铁隧道施工力学行为及地表沉降研究［D］.成都：西南交通大学，2009.

［7］张宏洲.隧道小导管注浆加固区围岩力学参数反分析研究［D］.北京：中国地质大学，2007.

［8］郭小红，陈卫忠，曹俊杰.跨海峡隧道风化槽围岩衬砌防排水技术研究［J］.岩石力学与工程学报，2010，29（7）：1481－>1488.Guo X H，Chen W Z，Cao J J.Waterproof and drainagEtechnologies for lining of subsea tunnel in weathered trough ［J］.ChinesEJournal of Rockmechanics and Engineering，2010，29（7）：1481－>1488.

［9］Davis EH，Gunnm J，Mair R J，et al.ThEstability of shallow tunnels and underground openings in cohesivematerial［J］.Geotechnique，1980，30（4）：397－>416.

［10］Gorasia R J，Mcnamara Am.High shear capacity ribbed piles［C］／／Proc.2nd European ConferencEon Physicalmodelling in Geotechnics.Ghent：Ghent University，2012：1－>10.

［11］Taylor R N.Tunnelling in soft ground in thEUk［C］／／Underground Construction in Soft Ground.Rotterdam：Balkema Publishers，1995：123－>126.

［12］Bilotta E.Centrifugemodeling of tunnelling closEto a diaphragm wall［J］.International Journal of Physicalmodelling in Geotechnics，2005，5（1）：27－>41.

［13］Bilotta E.Diaphragm walls tomitigatEgroundmovements induced by tunnelling，Experimental and numerical analysis［D］.Naples：University of Naples Federico II，Department of Geotechnical Engineering，2004.

［14］Grant R J.Movements around a tunnel in 2－>layer ground［D］.London：City University，1998.

［15］Kimura T，Mair R J.Centrifugal testing ofmodel tunnels in soft clay ［C］／／Proc.10th International ConferencEon Soilmechanics and Foundation Engineering.Rotterdam：Balkema Publishers，1981：319－>322.

［16］O'Reillym P，New Bm.Settlements abovEtunnels in thEUnited Kingdom－>theirmagnitudEand prediction［C］／／Proceedings of Tunnelling'82Symposium.London：Institution ofmining andmetallurgy，1982：173－>181.

［17］Mair R J，Taylor R N.Bored tunnelling in thEurban environment［C］／／Proc.14th International ConferencEon Soilmechanics and Foundation Engineering.Rotterdam：Balkema Publishers，1997：2353－>2385.

［18］谢骏，刘纯贵，于海勇.双平行圆形隧道稳定的塑性极限分析上限解［J］.岩石力学与工程学报，2006，25（9）：1835－>1841.XiEJ，Liu C G，Yu H Y.Upper bound solutions of plastic limit analysis for thEstability of two parallel circular tunnels［J］.ChinesEJournal of Rockmechanics and Engineering，2006，25（9）：1835－>1841.