基于改进蚁群算法的无人机二维航迹规划和重规划

唐必伟，方 群

（西北工业大学 航天学院，陕西 西安 710072）

航迹规划是指在特定约束条件下寻找运动体从起始点到终点满足某项性能指标最优的运动轨迹[1]。基本蚁群算法能够找到飞行航迹的可行解，并且具有较好的鲁棒性，但容易陷入局部最优，并且求解时消耗时间较长，在求解大型问题上相对比较弱[2]。针对基本蚁群算法的缺点，文中通过引入伪随机状态转移规则，对基本算法进行改进，该方法的最大的好处就是能够使算法在较短的时间里尽快收敛到最优解附近，使得算法耗时较少，同时可以避免局部最优。因为无人机在执行特定任务的过程中，由于飞行区域异常复杂多变，为了提高无人机在执行任务过程中的生存概率，文中通过引入动态窗口对无人机在碰到突发威胁的过程中进行航迹重新规划。

1 航迹的描述

1.1 飞行区域模型

如图1所示，将飞行区域划分成由个单元格组成的正方形区域，形成连接起始点到飞行目标点的网络图。飞行器在网格中的节点上飞行。将威胁源（包括雷达、防空高炮阵地等）视为半径为的圆。在该正方形区域中建立二维坐标系，飞行起点坐标（0，0），飞行终点坐标为（，0），待选节点的生成和选择原则参考文献[2]，即将距离当前飞行节点最近的5个节点作为待选节点。

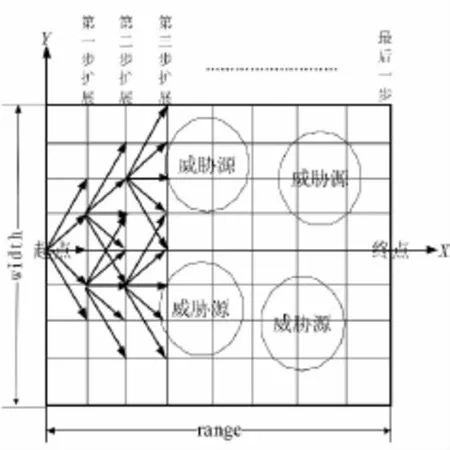
图1 飞行区域模型Fig.1 Model of fligth area

1.2 航迹规划目标函数

文中采用低于某一探测指标，而且具有可接受航程的航迹作为任务航迹，按最小航程和最小可探测性航迹加权方法计算代价函数作为描述航迹的性能指标。因为在建立飞行区域模型的时候将连续的飞行区域进行了离散化，无人机在航迹节点进行飞行，所以在计算航迹目标优化函数的时候以每条航迹上两相邻节点组成的航迹边为对象计算航迹边的代价，然后将整条航迹进行所有的航迹边进行求和。具体航迹代价函数为：

其中：F（R）是整条航迹的综合代价函数；N是该航迹所包含的节点个数；（i，j）是该航迹上相邻两节点；是两相邻节点所组成的航迹边的航程是这两相邻节点所组成的航迹边的威胁代价；k是权重系数，本文中k=0.5。文中关于航迹边的威胁代价通过下面的这个表达式求得：1/min （l1，l2，l3…lthreatnum）。 其中 l1，l2，l3…lthreatnum为节点 j到这威胁圆圆心的距离。

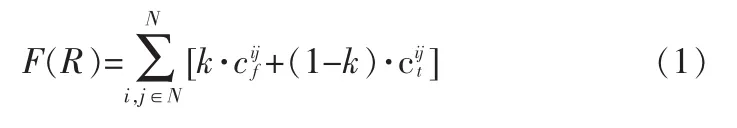
2 改进蚁群算法

2.1 伪随机状态转移规则

飞行器从一个节点转移到另外一个节点是由式（2）依照概率进行的：

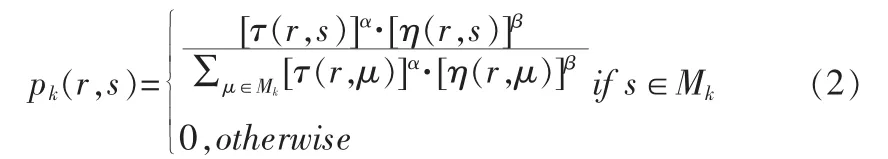
而伪随机状态转移规则可以表述为式（3）：

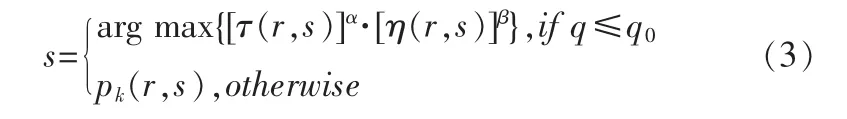
其中：pk（r，s）、τ（r，s）、α、β 分别表示节点 r转移到节点 s的概率、节点r到节点s航迹段的信息素浓度、信息素重要因子、能见度重要因子；η（r，s）是节点s相对于节点r的能见度，文中为两节点距离倒数； arg max{[τ（r，s）]α·[η（r，s）]β}函数的作用是返回{[τ（r，s）]α·[η（r，s）]β}数值为最大的节点 s 的值；Mk是待选节点候选集合；q0是触发参数；运用伪随机状态转移规则使搜索方向更倾向于最优解方向，从而更有利于得到最优解。

2.2 信息素更新规则

蚁群算法中信息素更新规则可以通过式（4）来确定：

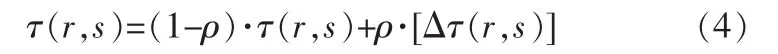
其中：

其中：antnum表示蚂蚁总数；Q是给定的常数；ρ表示信息素挥发系数，取值范围为 0～1；Δτ（r，s）是本次循环中航迹边（r，s）上总的信息素增量；Δτk（r，s）是本次循环中航迹边（r，s）上由第只蚂蚁所带来的信息增量；wk在文中表示本次搜索中的最优航迹的航迹代价值。

2.3 改进的蚁群算法在二维航迹规划中的应用

下面的步骤主要给出了改进蚁群算法在无人机二维航迹规划中的应用步骤：

1）初始化初始参数（包括蚂蚁的总数、飞行区域的节点数目、迭代的次数等等初始参数）；

2）初始化飞行节点信息素，形成信息素初始矩阵，信息素初始值设为2，将在威胁源里面的节点信息素初值赋为0，以确保飞行器在搜索过程中避开这些节点；

3）按照式（2）和式（3），从起始位置逐点进行剩余节点转移，直到到达目标位置；

4）找到本次循环中的最优路径，利用式（4）、式（5）、式（6）对最优路径上的节点进行信息素更新；

5）判断是否达到指定迭代次数，如果到达则输出最优路径的解。如果不是，则跳转到第3步进行循环迭代。

2.4 改进的蚁群算法在二维航迹重规划中的应用

通过前面介绍的方法可以很好地得到无人机二维全局航迹，全局航迹的规划是根据已知的威胁源信息离线完成的，并装载在无人机上作为飞行的参考航迹。如果在飞行过程中遇到了事先没有确定的威胁源，就要进行航迹的在线重新规划。当无人机探测到新的威胁并且确定威胁范围后，选择一个合适的动态窗口，要求此窗口包含新探测到的威胁源所包含的范围和此范围内的全局航迹，并对局部航迹进行重规划，尽量保证飞行航迹的性能指标最优，下面介绍一下动态窗口。

动态窗口[4]：当飞行器在某时刻探测到新威胁源的位置和该威胁源包括的范围后，选择一个大小合适的窗口，此窗口包含了新探测到的威胁范围和此范围内包含的全局航迹，动态窗口包含的范围就是航迹重规划的区域大小。动态窗口其实就是一个大小可变的规划区域，只是这个区域的大小是由新探测到的威胁源的位置和新威胁源覆盖的范围决定的，当窗口选得越大的时候重规划效果越好，但算法也越耗时，当动态窗口选择稍小的时候重规划效果稍差，算法越节省时间。

下面介绍一下文中介绍的蚁群算法在无人机二维航迹重规划中的应用步骤：

1）无人机探测新威胁的位置和威胁范围，假设新威胁源的中心坐标为，威胁半径为；

2）判断新的威胁源与机载的全局航迹有没有交点：如果没有交点就不需要进行航迹的局部重规划，无人机还是按照机载的全局航迹飞行；如果有交点则转至步骤3）；

3）求出新威胁源与机载全局航迹的交点，假设为（xstart，ystart），（xend，yend），根据这两个交点确定动态窗口的起点和终点分别为（xstart－window，ystar－window），（xend－window，yend－window），其中window是一个事先给定的常数，一般取4～5之间的整数，window的数值越大表示动态窗口越大，重规划效果也越好，但是所需要的时间也越长。

4）根据动态窗口的起点和终点确定需要进行航迹重规划的区域，动态窗口的起点和终点就是局部航迹规划区域的起点和终点，确定了局部航迹规划的起点和终点后就可以参考类似全局航迹规划的算法，利用改进的蚁群算法进行动态窗口飞行区域里航迹的重规划；

5）当动态窗口里面的局部航迹重规划后，将这个区域里面的局部航迹替代原来机载的这个范围里面对应的全局航迹，保证无人机可以成功的回避新探测到的威胁。

3 仿真分析

3.1 改进蚁群算法与基本蚁群算法仿真结果对比分析

仿真设初始参数为：

antnum=20，Q=10，repeat=100，α=5，β =3，Rmax=150，ρmax=0.8，ρmin=0.2，q0=0.7。仿真结果如图2～图3所示。图中实线代表改进蚁群算法的仿真曲线，虚线代表基本蚁群算法仿真曲线。对于航迹的光滑可以采用如下方法处理：当得到的最优航迹所包含的两个节点的连线段不穿过威胁源，同时在转折点处满足最小转弯半径rmin限制时，就将两节点用直线段连接，否则就保留原来航迹，文中rmin=1。

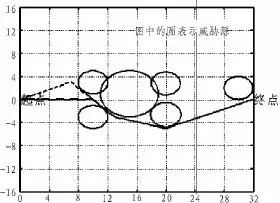
图2 6个威胁源下航迹Fig.2 Route under six threats

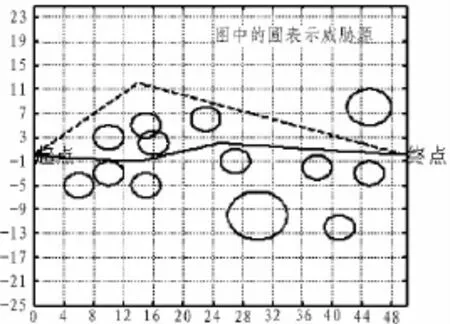
图3 13个威胁源下航迹Fig.3 Route under thirteen threats

为了进一步比较，下面的表另外给出了两种方法在不同威胁源分布情况下的最优解和收敛时间记录，其中试验1是文中的方法得到的结果，试验2是基本算法得到的结果。

3.2 改进蚁群算法在二维航迹重规划中的仿真示例

初始条件同上，取window=4，重规划的迭代次数repeat1=20，新探测到的第一个威胁源圆心为（15，1），威胁半径为 r=4，第二个威胁源圆心为（36，1），威胁半径为 r=4。进行仿真，结果如图4所示，其中黑色虚线表示离线规划好的全局航迹，黑色实线表示重新规划后的航迹，实线圆表示离线探测到的威胁，虚线圆表示新探测到的威胁源。

表2记录了该仿真实验组的数值结果，具体如下：

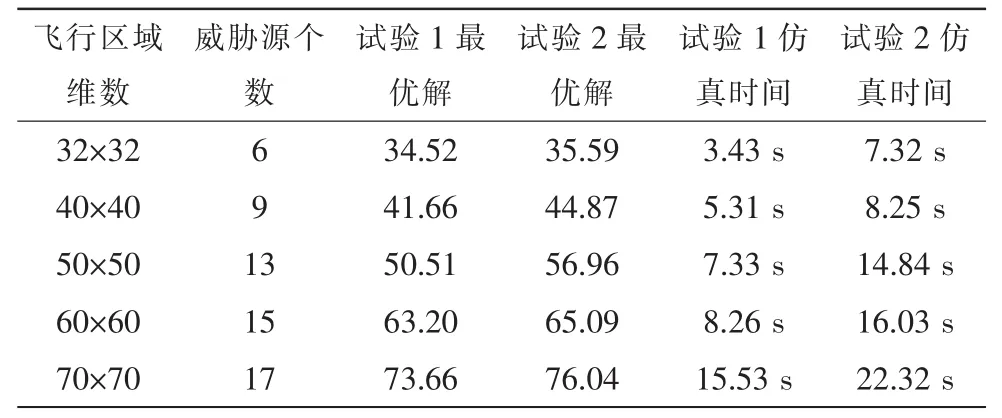
表1 不同初始条件下不同方法得到的结果对比Tab.1 Comparing of result on different initial conditions using different method

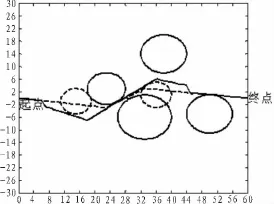
图4 重规划航迹Fig.4 Replanning route

表2 重规划航迹结果记录Tab.2 Result of replanning route

4 结 论

通过引入伪随机状态转移规则对基本蚁群算法进行改进，并将改进的算法应用到无人机二维航迹规划上。为了提高无人机在变多的战场环境的生存概率，通过引入动态窗口的思想进行航迹重规划，最后给出了对应的仿真示例和相应的仿真数值结果。由前面的仿真结果可以看出，无论是基本蚁群算法还是改进蚁群算法都可以用在无人机航迹规划研究中，都能搜索到一条可行的航迹。但是从仿真曲线2和3可以看出在相同条件下，文中改进的蚁群算法搜索到的航迹比基本蚁群算法搜索到的航迹的最优解要好，从表1的数据中也可以看出利用本文改进的蚁群算法进行航迹规划的时候，无论是得到的航迹最优解还是算法耗时都要全面优于基本蚁群算法。从仿真曲线4可以看出通过动态窗口的引入，利用文中介绍的蚁群算法可以成功地为无人机进行航迹重规划，并从表2的仿真结果看以看出，利用文中改进算法进行航迹重规划的时候，算法耗时基本上满足实时性要求。

[1]郑昌文，严平，丁明跃.飞行器航迹规划研究现状与趋势[J].宇航学报，2007，28（6）；1441-1446.ZHENG Chang-wen，YAN Ping，DING Ming-yue.Research status and trend of route planning for flying vehicles[J].Journal of Astronautics，2007，28（6）：1441-1446.

[2]杨士勇，杨丹.基于改进蚁群算法的巡航导弹航迹规划[J].宇航学报，2007，28（4）:903-907.YANG Shi-yong，YANG Dan.Route planning of cruise missile based on improved ant colony algorithm[J].Journal of Astronautics，2007，28（4）:903-907.

[3]任波，于雷，韩李勋.自适应蚁群算法的无人机航迹规划方法[J].电光与控制，2007，14（6）:36-39.REN Bo，YU Lei，HAN Li-xun.On path planning for UAVs based on adaptive ant system algorithm[J].Electronics Optics&Control，2007，14（6）:36-39.

[4]徐伟龙，吴庆宪，姜长生.粒子群法在三维航迹规划及其优化中的应用[J].电光与控制，2008，15（5）:1-6.XU Wei-long，WU Qing-xian，JIANG Chang-sheng.Application of particle swarm algorithm in 3D route planning and optimization of air vehicles[J].Electronics Optics&Control，2008，15（5）:1-6.

[5]Stump E，Michael N.Multi-Robot Persistent Sur-veillance Planning as a Vehicle Routing Problem [C]//2011 IEEE International Conference，569-575.

[6]Reiners T，Pahl J，Maroszek M，et al.Integrated Aircraft Scheduling Problem:An Auto-Adapting Algorithm to Find Robust Aircraft Assignments for Large Flight Plans[C].45th Hawaii international Conference on System Sciences，2012：1267-1276.

[7]Bertuccelli L F，Cummings M L.Operator Choice Modeling forCollaborative UAV VisualSearch tasks[C]//IEEE Transactions on Systems，2012，42（5）:1088-1099.

[8]WANG Ting-song，ZHENG Peng-jun，LIU Zhi-yuan.Model and algorithm for a liner ship fleet planning problem with uncertain container shipment demand[C]//IEEE，2012，202-207.