基于动态加权TOPSIS方法的学习状况评价＊

李文涛 韩庆艳

（1.陆军军官学院 合肥 230031)（2.安徽邮电学院 合肥 230031)

1 引言

评价学生的学习效果是教学评价的重要环节［1］。客观、合理的评价是对学生阶段性学习的认可，可以起到激励的作用。随着素质教育的逐步深入，如何评价学生的学习状况成为我们在学生素质培养方面取得突破的当务之急。历年来，大部分学校对学生的学习评价，只是单纯根据学生的“绝对分数”或者“绝对排名”作为评价，这种评价方法仅能量化出学生的基础，而不能体现学生学习的稳定性、潜力、变化趋势等指标［2～5］。随着教学改革的不断深入，科学评价教学质量及学生学习效果极为重要［6］。

本文从学习成绩和进步情况两方面构建学习状况评价指标，考虑到各学期试卷难度不同，将各学期分数通过难度系数标准化，然后利用动态加权的理想点法建立评价模型，对学生的学习状况进行全面、客观、合理的评价。

2 评价指标选取与试卷难度系数确定

2.1 学习状况评价指标选取

评价学生学习状况的目的是激励优秀学生努力学习取得更好的成绩，同时鼓励基础相对薄弱的学生树立信心，不断进步。所以评价不能只对分数评价，还要从分数变化上考虑［7～8］。另一方面，因为题目只给了每名学生各学期的分数，从所给数据，本文只能确定出分数和分数变化两个能够直观地反映学生学习情况的方面，以四个学期成绩评价为例，选取的评价指标如图1所示。

2.2 确定试卷难易系数

试卷质量的高低体现在试卷的区分度上，为了使得试卷难度系数的计算更加合理，需要在去除试卷无区分度分数后，再对难度系数进行考虑［9～10］。

图1 学习情况综合评价指标体系

1)突出试卷区分度的影响。假设每学期考最低分学生得到的分数是每个学生都能得到的，最高分学生得不到的分数是每个学生都得不到的，所以，各学期考试有区分度的分数的有效区间为［Li，Hi］（i＝1，2，3，4)，将有区分度的得分化为百分制：

2)计算各学期试卷的难易系数。在式（1)中得到每名学生有效得分的基础上，利用表的数据，本文运用极端分组法计算各学期试卷的难度，一般通过以下步骤：

step1：按考试得分排列试卷；

step2：确定高分组：从得分最高的一份试卷开始依次向下选出全部试卷的25%，作为高分组；

step3：确定低分组：从得分最低的一份试卷开始依次向上选出全部试卷的25%，作为低分组；

step4：按下列公式计算难度：

3)根据试卷的难易系数对各学期分数进行转换。得到各学期难度系数后，将各学期的得分除以个学期试卷的难度系数：

3 基于动态加权TOPSISI方法的学习状况

TOPSIS方法是一种逼近理想解的排序方法，其基本思想是把综合定量评价的问题转化为求各评价对象之间的差异—“距离”，即按照一定的法则先确定理想解与负理想解，然后通过计算每一个被评价对象与理想解、负理想解之间的距离，再经过比较得出综合评价。

3.1 变异系数法确定指标权重

不同指标对学习状况评价的贡献有差异，所以需要对各指标的权重进行分析。变异系数法是客观赋权法的一种，它克服了比如层次分析法的主观赋权法的主观性。结合本问题，其步骤如下：

step1：计算各指标的平均值和标准差。平均值反映指标的平均水平；标准差反映指标的绝对变异程度。

step2：计算各指标的标准差系数，即相对变异程度，公式如下：

step3：对标准差系数进行归一化处理，确定各指标的权重。

3.2 基于理想点法的学习状况评价

step1： 评价指标的极性处理，得到极性一致化矩阵R＊。由于所取指标都是极大型（指标越大，学生学习状况评价越好)，步骤一省略。

step2：评价指标的规范化处理。通过极差变换得到规范化矩阵X＝（xij)m×n，即

其中xij是无量纲的量，且

step3：构造加权规范决策矩阵Z。依据上一节变异系数法确定7个指标的权重矩阵W，令

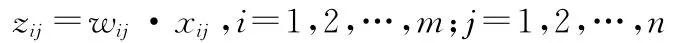
step4：确定正理想解z＋及负理想解z。设正理想解z＋的第j个属性值为z＋j，负理想解z的第j个属性值为zj，则取正理想解为

负理想解为

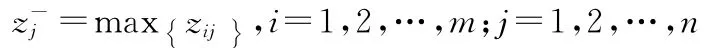
step5：计算距离。被评价的对象到正理想解的欧式距离为

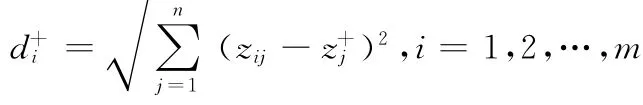
被评价的对象到负理想解的欧式距离为

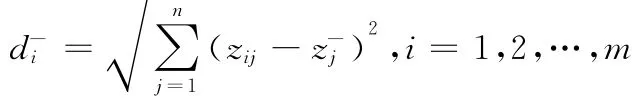
step6：求综合评价值。被评价的对象的综合评价指标值为

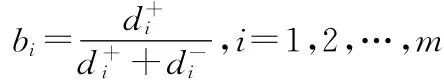
4 实例分析

现有某学校的612名学生四个学期的学习成绩调查数据，对所得数据进行统计可知在四个学期中出现两人次考试成绩为0分，对0分成绩默认为缺考，在该学期内不算入参考人数。统计结果如表1所示。

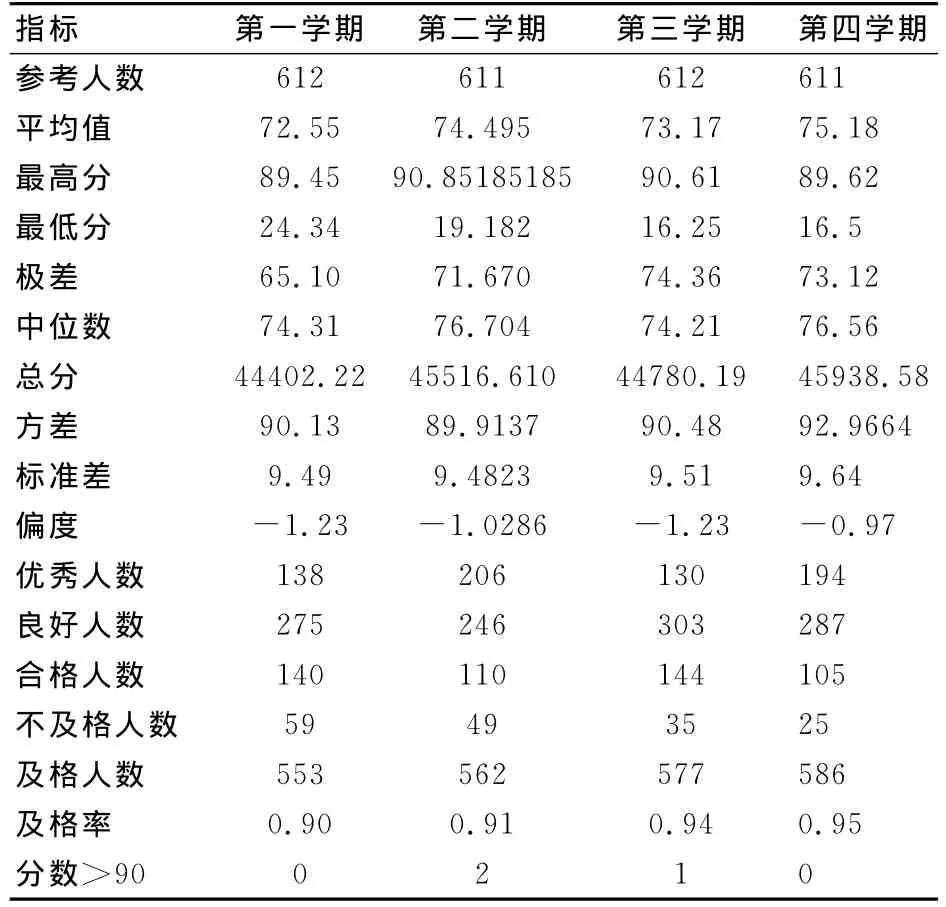
表1 612名学生四学期成绩统计表

下面根据本文所给的方法对学习状况进行评价。首先分析试卷难易程度，根据2.2中步骤对数据进行处理，得到各学期试卷的难度系数，见表2。

表2 各学期试卷的难度系数

根据试卷的难度系数对个学期分数进行转换，转换后的成绩见表3。

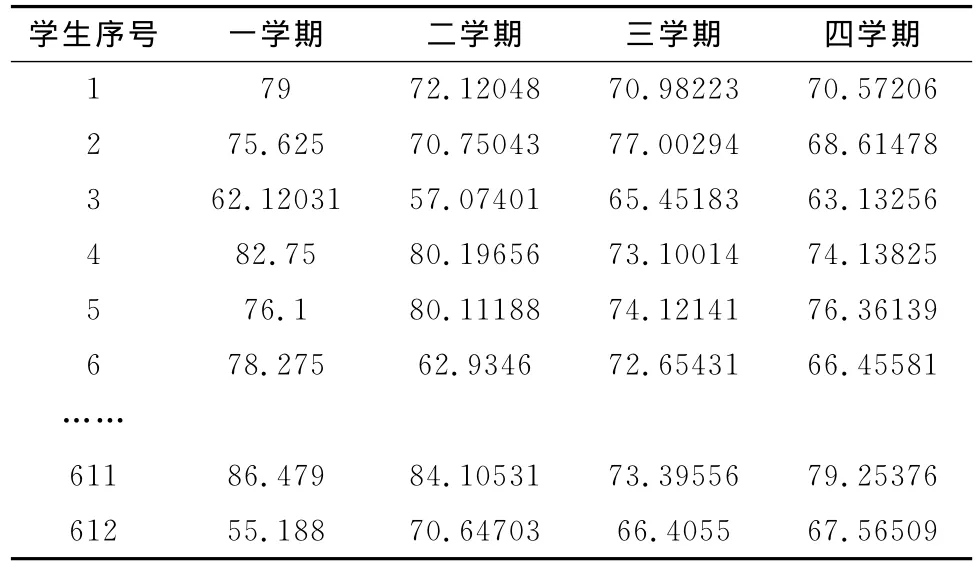
表3 统一难度标准后学生的得分

以上工作使得四个学期的考试成绩在同一难度标准下表示出来，为评估过程消除了障碍。通过变异系数法，求得各指标的权重见表4。

利用Matlab编程求出每名学生的综合评价值如表5。

各项指标越大，被评价学生的状态越接近正理想解，其综合评价值越大，学习状况越好；反之越接近负理想解；综合评价值越小，学习状况越差。对学生进行排名，见表6。

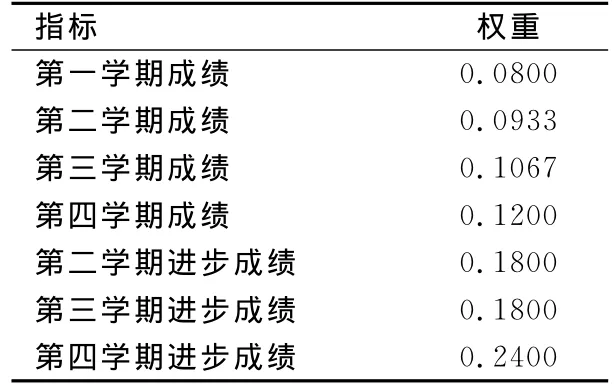
表4 各指标权重

表5 每名学生的综合评价值

表6 学生学习状况排名

5 结语

本文根据试卷的难易系数对各学期分数进行转换，避免了因试卷难易不同所造成的误差，从学生成绩和进步情况两方面构建学生学习状况评价指标体系，然后用变异系数法，依据数据之间的关系来确定权重，具有较强的数学理论依据，使决策结果更真实可靠，最后运用TOPSIS法进行评价，经过实例验证，排序结果反映了不同评价对象的优劣程度。

［1］李恒，郭石磊，时红霞.学生成绩评定方法研究［J］.重庆工学院学报，2006，20（6)：167170.

［2］王理.考试分数与学业成绩评价［J］.内蒙古师范大学学报，2001（5)：4245.

［3］冯祖琴，徐娟.建立健全考试和成绩评价体系，推进高校考试管理改革［J］.教育探索，2010（3)：4742.

［4］吴翠兰.关于学生考试成绩的分析与评价［J］.北京工业职业技术学院学报，2003（4)：6265.

［5］金鑫，李扬，孙国庆等.学生成绩评价数学建模［J］.辽宁工程技术大学学报，2010，（S1)：176178.

［6］谷峰.学习水平的标准评价模型及应用［J］.数学的实践与认识，2010，40（24)：1521.

［7］程久苗，朱永恒.高师地理科学专业野外实习成绩评价指标与评价方法探讨［J］.安徽师范大学学报，2009（4)：8994.

［8］谷峰.试卷水平的标准化定量评价［J］.数学的实践与认识，2011（11)：2428.

［9］李因果，李新春.综合评价模型权重确定方法研究［J］.辽东学院学报，2007（2)：2428.

［10］吴维宁，高凌飚.学业评价模式的初步研究［J］.华南师范大学学报，2005（6)：8791..