多机超视距协同空战协同力学模型研究＊

陈 正 李田科

（1.海军航空工程学院指挥系 烟台 264001）（2.91980部队 烟台 264001）

1 引言

超视距协同空战是以空战胜利为目标，以信息、决策、火力为中心，在多种因素的竞争与协同相互作用下，最终实现空战多机、多编队之间的整体效应[1～3]。国内国外的很多文献都对协同空战中的目标搜索[4～5]、目标识别[6]、态势评估[7～8]、威胁估计[9～12]、目标分配[13～19]和效能评估[20～22]做了系统而深入的研究，从多个方面说明了空战中多机、多编队之间协同的作用和效果。但是这些相关的研究都没有从协同学理论的角度进行深入讨论，本文力图从超视距协同空战系统的角度入手，在深入理解协同学理论的基础上寻求各作战飞机之间的协同与合作，分析系统各协同主体之间基于协同的自组织，并提出协同空战的协同力学模型，为深入研究超视距空战协同的组织和管理“抛砖引玉”。

2 超视距协同空战协同性理解

超视距空战编队子系统由一组具有自治性、主动性、反应性等特征的战斗机组成，由于单架战斗机能力和资源受限，各机需要相互协同合作来完成空战任务，因此要构建一个有效的协同空战系统，需要详细分析和设计系统内的协同过程，通过多机之间的协同合作去研究解决一些复杂的优化问题。

假设有遂行超视距协同空战任务的系统X，有n个元素为x＝（x1，x2…，xn）∈X表示各战斗机，令所考察的系统功能为W，则有：

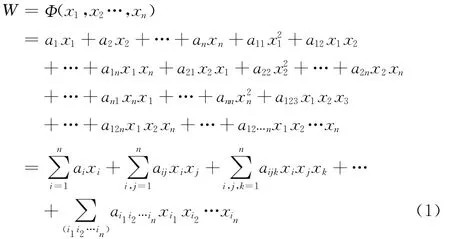
上式取的是n个元素的各种“排列式”，而一般协同空战系统只需取作“组合式”即可，即有[23]：

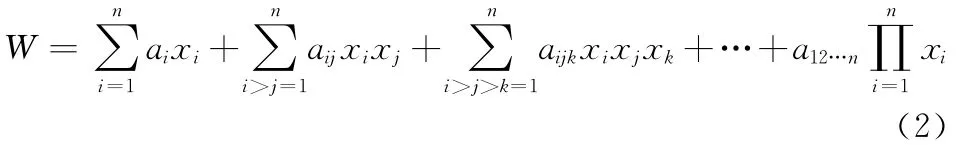
3 超视距协同空战中自组织模型

3.1 自组织概念

自组织是系统在没有任何外部指令或外力干预的情况下自发地形成一定结构和功能的过程和现象[25]。自组织现象是系统的建构及演化现象，系统依靠与外界交换物质、能量、信息而存在，且在相对稳定的状态下不断向结构化、有序化、多功能方向发展。

自组织包含三类过程：1）由非组织到组织的过程演化；2）由组织程度低到组织程度高的过程演化；3）在相同组织层次上由简单到复杂的过程演化。超视距协同空战系统的自组织属于后两种，本文研究的是超视距协同空战系统中各子系统之间的组织如何实现由组织程度低到组织程度高的过程演化，或者在相同组织层次上由简单到复杂的过程演化问题，即研究的重点是有序程度如何得以提升。

3.2 超视距协同空战系统的自组织与被组织

超视距协同空战的系统因其军事特色，从结构到功能都有着浓重的被组织“气息”。但是在空战时，从系统的角度来讲，已经和对空作战指控台位进行过权限交接的预警机和空中的各编队，可看成是没有任何外部干预的，在总的防空作战目标指导下自发与敌方来袭目标进行交战的系统。系统内的预警机和各战斗机在超视距协同空战原则的指导下，围绕防空作战任务目标自发地集聚，密切协同，形成有效的协同结构，自发地获取高质量、高实时性、高精度的信息，制定高质量的机动决策和战术决策，最终形成高效的协同火力输出，从而形成了一个由超视距空战信息到协同决策再到火力打击的价值链系统，这就是其系统的自组织性。而处在编队中的单架战斗机，则是“组织化”了的单元，具有“被组织”性。

超视距协同空战系统既有自然系统的自组织共性，也有其独特的个性，是一个既有自组织也有被组织因素建立起来的组织，在形成组织的过程中，被组织方式多于自组织方式。指挥和控制正是协同学中所说的对系统“施加外部压力”，通过这种“被组织”的方式促使系统更好地实现“自组织”过程。因此可以说，超视距协同空战系统自组织的实质就是在相关的超视距空战原则框架下，通过指挥和控制使系统有序程度得以提升，产生空战价值增值。

3.3 自组织模型

分析超视距协同空战包括组织协同和自组织协同两部分内容，在此主要进行自组织协同的建模与分析，揭示自组织产生的机理，为协同力学模型构建提供支持。

借用协同学构建自组织模型的数学方法，在建立超视距协同空战系统的自组织模型时，系统的详细运动或微观描述可以用一组一阶时间导数的常微分方程来表达。为研究问题简便起见，假定超视距协同空战系统只有一个双机编队，把各子系统（两架战斗机）的整体运作看作是一个变量，在此基础上，来建立超视距协同空战系统的自组织模型。

设：两架战机最初是两个无耦合系统，用来描述它们独自与外部环境的协调状态的状态变量为q1和q2，其中dq1／dt、dq2／t分别表示两个状态变量q1和q2随时间的变化率。

变量演化方程如下所示：

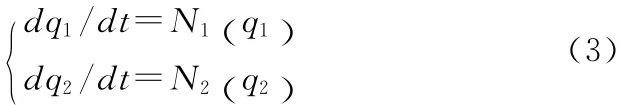
假设两架战机各自存在稳定的、符合q1和q2所描述的状态。认为两架战机在没有发生任何联系之前各自处于相对稳定状态，这种稳定状态可以表示为：q1＝0，q2＝0。

随着编队在空战中面临的威胁越来越复杂，各机将不断调整自己的状态，加强与外部的合作，此时两个系统发生了耦合关系，它由函数K1和K2所描述。两架战机的协调状态产生了一个q1＋q2的新系统，系统的组分数目也由原来的两个增加为三个，原来的两个无耦合的系统发生了耦合现象。新系统的运动方程为

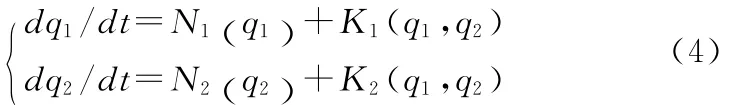
此方程组可转化为

其中，

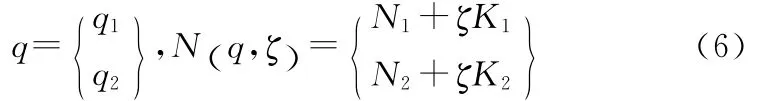
ζ∈ [0，1]，起控制参量的作用，代表两架战机之间的耦合程度，也即两架战斗机之间协同的自组织程度。为了便于表达，后文对自组织程度ζ简称为数值ζ。它的非零值反映出：比起ζ值为零时，协调状态的总系统组分数增加了，ζ值越趋近于1，越说明了两个系统的耦合程度在加深，自组织程度加深，它的变化可以导致方程组出现新的稳定解q≠0，表明超视距协同空战该节点处发生了某新类型的宏观结构或新的活动状态，协同度得到提升。

4 超视距协同空战协同力学模型

针对上节所述自组织模型，对于ζ的取值如何趋近于1，本文试图从理论力学的角度来探讨序参量对舰载战斗机超视距协同空战协同的影响。

图1中的虚箭头线表示实际超视距协同空战中可能存在的序参量，实箭头线表示本文研究所指的序参量（根据空战三要素信息、火力、机动），假设其中Fa表示信息协同程度，Fb表示协同机动的合理性，Fc表示协同火力，∑F表示的是合力。

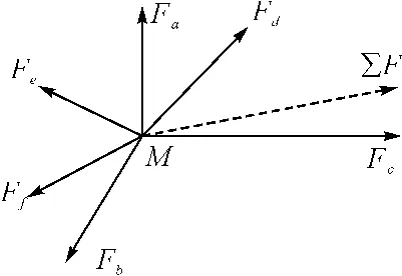
图1 在序参量作用下两系统协同程度的力学模拟示图

图1中M表示两系统的协同程度（耦合程度ζ），F表示序参量。在实际超视距协同空战系统中，序参量可能会多于或少于本文讨论的数目，上述讨论的序参量只是目前普遍存在的影响超视距空战协同的因素，具体研究时，应将所有的序参量都表述在图1中。

下面以Fa、Fb、Fc三个序参量的力学作用为研究对象，建立空间直角坐标系，从速度和加速度两个方面，对序参量如何施加作用力于子系统之间的关系进行深入探讨，建立起协同的力学模型。首先对该模型的建立作以下假定：

1）M点表示两架战斗机的自组织程度（耦合程度）ζ的形象模拟点。

2）在空间直角坐标系中，以Ox轴代表Fa的作用方向，Oy轴代表Fb的作用方向，Oz轴代表Fc的作用方向，M动点受∑F的作用，随时间t单调连续地变化，方程组可以表示为x＝f1（t），y＝f2（t），z＝f3（t） （7）

3）M点在Fa、Fb、Fc三个序参量的作用力下，有各自方向上的运动速度vx，vy，vz，以及对应的加速度ax，ay，az，从而使得M动点获得一个综合的力∑F、速度v和加速度a。

4）由于M点受到合力∑F的作用，其产生的速度v和加速度a决定了它会随着时间t的变化，在序参量的共同作用下向一个更协调、更有序的趋向运动发展，从而使得上一个模型中的耦合度ζ不断趋近于1。

空间直角坐标系Oxyz如图2所示。式（7）是M点的空间直角坐标形式的运动方程，也是M动点轨迹的参量方程，可以用M动点的直角坐标来表示它的矢径。

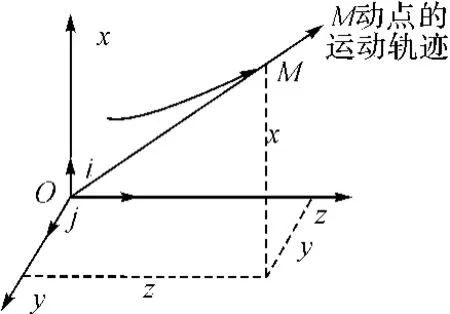
图2 空间直角坐标系法中M动点的运动轨迹

设i，j，k分别为沿着坐标轴Ox、Oy、Oz的单位矢量，则矢径是

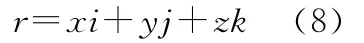
已知M动点在瞬时t的速度为加速度为根据式（9）、式（10）可得

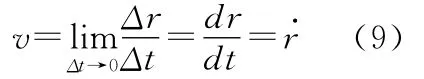
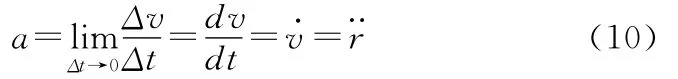
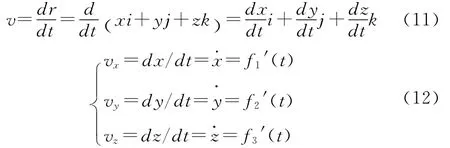
单位矢量前面的系数就是速度v在相应坐标轴上的投影，如图3所示，其表达式为

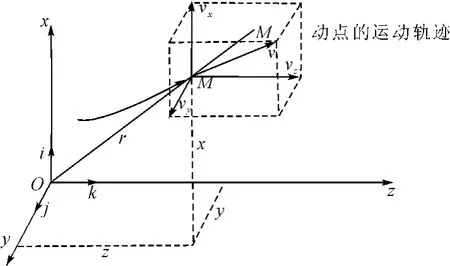
图3 空间直角坐标系法中M动点的速度v

式（12）表示M动点的瞬时速度在各直角坐标轴上的投影等于M动点相应的坐标对时间的一阶导数。由此即可以求出速度v的大小和方向余弦：

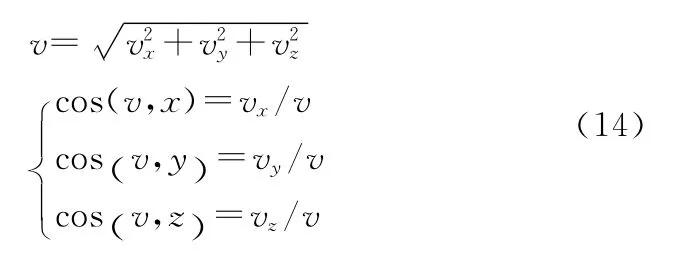
加速度为

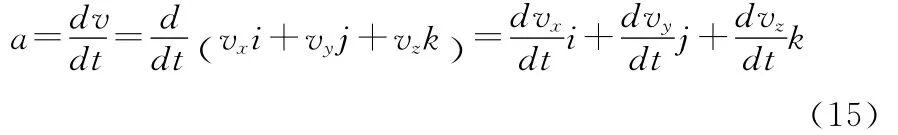
单位矢量前面的系数就是加速度a在相应坐标轴上的投影如图4所示。

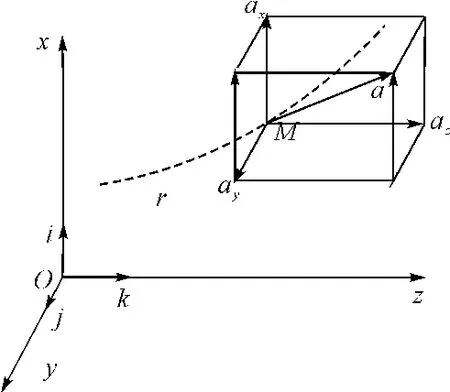
图4 空间直角坐标系法中M动点的加速度a

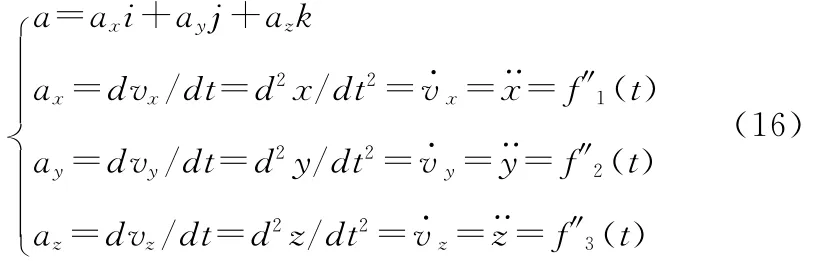
上式为M动点的加速度在直角坐标轴上的投影，等于M动点速度的相应投影对时间的一阶导数或M动点的相应坐标对时间的二阶导数。故加速度a的大小和方向余弦为

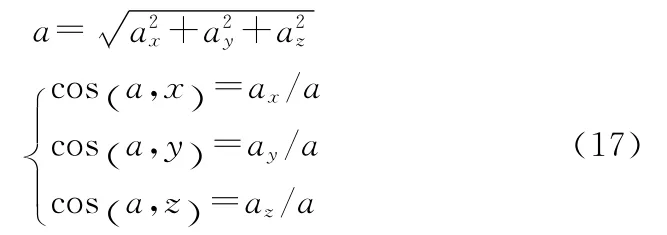
从方程（3）至方程（17）一系列方程和方程组，组成了超视距协同空战协同的力学模型数学表达式。其中，方程组（3）的建立是量化分析两架战斗机协同程度发展变化的基本前提。关于t的方程应该都是二次以上的方程，如果这个方程组都是三次以上方程组成的话，M动点的速度v及加速度a就可以各自表示成关于自变量t的单变量方程，从而也就可以绘出其曲线图的形式，这样更容易观察出v、a与t之间的关系，可进一步推出它们与耦合度ζ之间更明晰的量化关系；如果有方程只是一次的，表示其加速度为零，协同关系在这个坐标轴对应的序参量作用力下匀速运动；如果方程是常数的话，速度为零，表示此时协同关系处于静止状态，没有运动的迹象。

5 结语

从上述的模型可以看出，三个序参量Fa、Fb、Fc的方向和大小决定了M动点的坐标方程，决定了M动点速度的大小及方向，也即决定了超视距协同空战系统的协同程度和协同运动的方向。在研究具体超视距协同空战协同运作的实际应用中，可通过采集和输入大量真实的数据和信息，得到具体的速度v、加速度a以及a的大小，从而更清晰地观察到超视距协同空战系统的协同运作状况。在本文的研究中，由于实际资料的欠缺和理论应用上的困难，无法对模型进行实际应用模拟，只是从概念上提供一套超视距协同空战系统协同运作的描述性方法。在超视距协同空战的具体实践中，可根据这样的思路构建符合实时战况的协同模型，建立可行的模型的数据体系，为把握超视距协同空战协同运作，采用有效地被组织（指挥控制）手段提供依据。

[1]蓝伟华，喻蓉.多机编队协同空战的概念及关键技术[J].电光与控制，2005，12（6）：12－15.

[2]卢鹏，王瑾.面向第四代战斗机的超视距空战[J].火力与指挥控制，2009，34（6）：154－157.

[3]傅攀峰，罗鹏程，周经伦.空战武器体系超视距空战能力指标研究[J].系统工程与电子技术，2004，26（8）：1072－1075.

[4]高坚，佟明安.编队协同对空目标探测及搜索力的最优分配[J].系统工程与电子技术，2004，26（3）：350－352.

[5]张欧亚，佟明安，钟麟.不确定环境下编队协同搜索力最优分配[J].电光与控制，2007，14（2）：1－3，11.

[6]朱方，王付明.基于模糊信息论的空中目标识别模型研究[J].指挥控制与仿真，20062811－5.

[7]刘栋，谷志勇，任波，等.电子对抗环境下的多机协同空战态势评估方法[J].电光与控制，2008，15（7）：30－33.

[8]滕鹏，刘栋，张斌，等.超视距协同空战态势评估方法研究[J].电光与控制，2008，15（10）：47－50.

[9]董彦非，郭基联，张恒喜.多机空战目标威胁评估算法[J].火力与指挥控制，2002，27（4）：73－77.

[10]俞卫树，姜长生.基于E1man神经网络的空战威胁排序研究[J].电光与控制，2008，15（8）：1－3.

[11]王俊，姜长生.基于LSRBF神经网络的空战目标威胁评估[J].电光与控制，2007，14（4）：43－45.

[12]蓝伟华，陈晓风.单机多目标攻击的目标威胁排序[J].电光与控制，2006，13（5）：16－17，30.

[13]高 永，向锦武.超视距多机协同空战目标分配算法[J].北京航空航天大学学报，2007，33（3）：286－289.

[14]孙金标，范方军，徐荣红.编队空战的目标分配研究[J].飞行力学，2006，24（3）：89－93.

[15]柳毅，佟明安.匈牙利算法在多目标分配中的应用[J].火力与指挥控制，2002.27（4）：34－37.

[16]王宗虎，徐圣良，王焕章，等.舰载航空兵超视距攻击的目标分配优选模型[J].舰船电子工程，2008（10）：10－13.

[17]GENG Yan－luo，JIANG Chang－sheng，LI Wei－hao.Multi－Fighter Coordinated Multi－Target Attack System.Transactions of Nanjing University of Aeronautics ＆ Astronautics，2004.12（1）：18～23.

[18]嵇亮亮，姜长生.基于协同攻防的多机空战目标分配及排序[J].电光与控制，2008，15（9）：14－17.

[19]LUO De－Lin，SHEN Chun－Lin，WANG Biao，WU Wen－Hai.Air Combat Decision－Making for Cooperative Multiple Target Attack：An Approach of Hybrid Adaptive Genetic Algorithm.Journal of the Graduate School of the Chinese Academy of Science，2006，（3）：58－60.

[20]穆富岭，罗鹏程，马元正.编队超视距空战效能评估方法[J].火力与指挥控制，2006，31（12）：91－93.

[21]董小龙，孙金标.灰色关联综合优化法评估超视距空战效能[J].飞行力学，2009，27（1）：85－88.

[22]华玉光，徐浩军，唐铁军，等.编队战斗机超视距空战效能评估[J].火力与指挥控制，2006，31（6）：15－18.

[23]高隆昌.系统学原理[M].北京：科学出版社，2005：1－2.

[24]粘松雷，林云，陈榕.基于改进BP算法的编队空中威胁判断模型研究[J].计算机与数字工程，2011（12）.

[25]郭治安，沈小峰.协同论[M].山西：山西经济出版社，1991：91－95.