同轴腔体窄带带通滤波器快速设计方法

张 强，张贞鹏，李 伟

（1.中国电子科技集团公司13所，石家庄050051；2.空军驻石家庄地区军事代表室，石家庄050051）

0 引 言

微波滤波器是雷达系统、卫星通信系统、测量系统等必不可少的组成部分，一般被用来分开或整合不同频段的信号［1］。随着通信设备研制周期的缩短，对于滤波器这种不能系列化生产的产品研制速度提出了很高要求。对于腔体滤波器来说，目前的设计方法都是使用仿真软件对滤波器进行电磁仿真，然后再进行实物加工调试。由于三维电磁仿真计算量大，目前的硬件条件还不能支持快速的仿真设计，所以使得研制周期中的相当一部分时间花费在仿真计算中，影响了研制周期。

为了缩短同轴腔体滤波器的仿真时间，本文提出了一种使用三维电磁仿真软件和电路仿真软件结合使用的设计方法，可以提高滤波器的设计速度。最后对该设计方法进行验证，证明该方法的正确性。

1 设计方法理论分析

同轴腔体窄带带通滤波器的模型图如图1所示，它可以看做一系列谐振腔的组合。每个谐振杆代表一个谐振腔，谐振于滤波器的中心频率附近；谐振腔的谐振频率决定滤波器的中心频率，Q值影响滤波器的插入损耗［2］。耦合膜片控制相邻谐振腔的耦合量，端口处的探针决定滤波器与外界的耦合，耦合量决定滤波器的带宽。所以在设计滤波器的过程中，重点设计单个谐振腔的谐振频率、Q值以及各个谐振腔之间耦合量和边缘谐振腔与外界的耦合。

谐振腔上的调谐螺钉用于调试滤波器的谐振频率，因为该螺钉的作用等效为1个电容，所以也成为电容加载。螺钉深入的长短反映了电容加载的大小。在后续的设计过程中，将该螺钉的长度放在二维仿真软件（ADS）中进行优化。所以快速设计方法的本质就是将3D电磁（EM）软件中的模型S参数提取到电路仿真软件中，使用集总元件对电容加载的量值进行优化。

1.1 根据设计指标确定滤波器的初值

已知滤波器的中心频率、带宽、插入损耗、波纹、带外抑制度等，通过原型滤波器查表可以计算滤波器节数、耦合常数、群时延、单腔谐振频率、单腔Q值［3－4］等：

式中：w1和w2为滤波器的通带边缘频率；Δw为滤波器的相对带宽；gi、gj为原型滤波器值；Kij为第i谐振腔和第j谐振腔之间的耦合系数；Qe为滤波器与外界的耦合系数。

考虑到使用查表和计算的方法相对麻烦，为了方便，可以将计算过程编入Excel中，如图2所示。通过输入已知参数，就可以很轻松地得到滤波器节数、耦合常数、群时延、单腔谐振频率、单腔Q值等参数。

图2 Excel计算初始值

1.2 确定单个谐振腔的结构

根据1.1中单腔谐振频率、单腔Q值以及对滤波器体积的要求，设计出单个谐振器的结构。通过3DEM仿真软件的本征膜方法可计算谐振腔的谐振频率和Q值，保证可实现最终的设计目标。

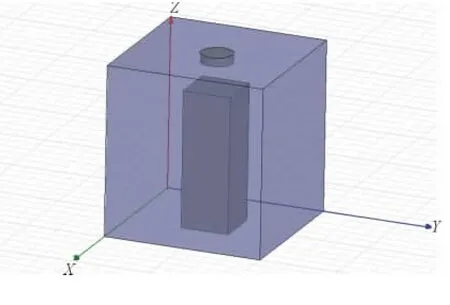
图3 CST软件仿真

根据图3的结构模型，在谐振腔的顶部加入集总参数电容，分别仿真谐振腔谐振频率。在相同谐振频率下得到螺钉长度和加载电容值的对应关系，如图4所示。

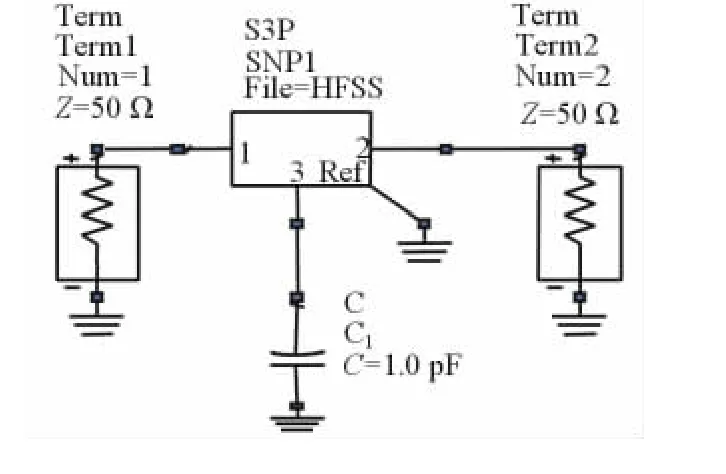
图4 电容加载电路仿真

1.3 端口和耦合系数的三维实现

此部分是关键所在，主要使用CST软件强大的场计算功能、ADS软件的电路计算和优化功能。

1.3.1 相邻腔体耦合系数确定

2个相同的腔体模型放在一起，如图5所示。中间通过缝隙连接，使2个腔体中的电磁能量可以交换，便构成了耦合。其中耦合分电耦合与磁耦合，即电容耦合与电感耦合。

图5中2个同轴腔体中间开缝，缝宽改变就可改变耦合系数。先设xz面（即缝所在的面）为电壁，用本征模解算器求出第1个模式的谐振频率，令其为fe；再设xz面为磁壁，算出第1个谐振频率，令其为fm，于是2个谐振腔之间的耦合系数K可由下式得出：

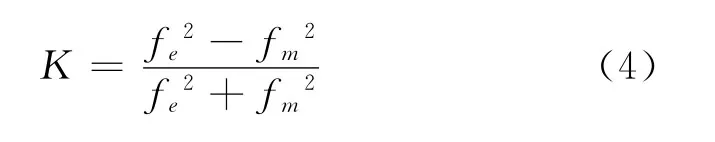
图5 相邻腔体耦合系数仿真

1.3.2 端口抽头高度的确定

边腔与外界的耦合是用K01和K45来表示的，在操作中，只需用群时延t1就可以了。t1可以从低通滤波器原型滤波器g值和相对带宽Δω计算得出：

如图6（a）所示，通过调整耦合圆盘伸入的长度和内导体的高度，使群时延最大值位于f0＝2GHz处，且其最大值与t1＝22.7ns相等，这样就可以确定抽头的高度，调好的群时延如图6所示。

1.4 整体模型仿真和优化

滤波器的全部主要参数已经得到，在3DEM仿真软件中进行整体建模，此时该滤波器除了具有输入、输出端口外，还应该在每个谐振腔的顶端加入端口，将仿真的SnP文件导出。

在电路仿真软件ADS中建模，采用S参数仿真方法，使用从3DEM仿真软件中导出的SnP文件，并在对应谐振腔的端口上加入对地耦合电容。优化耦合电容可以得到需要的滤波器曲线。

对照1.2节中的数据可得到每个调谐螺钉的深度，从而得到三维仿真软件中的滤波器结构参数。

2 设计实例

下面用一个设计实例来说明上面的设计过程。

2.1 设计指标

工作频率：670～720MHz；1dB 带宽：≥50MHz；插损：≤1dB＠670～720MHz；驻波：≤1.5＠670～720MHz；带外抑制：≥40dBc＠DC～635MHz＆745～1 500MHz。

2.2 滤波器初始值

根据查表看出6节滤波器可以实现该参数，单腔谐振器Q值为3 000时，插入损耗为0.11dB，考虑上波动，可以满足指标要求。表1、表2及表3是原型滤波器值、耦合系数和插入损耗以及群时延的原始参数。

图6 抽头仿真

表1 原型滤波器值

表2 耦合系数和插入损耗

表3 群时延

2.3 端口和耦合系数的三维实现

图7 耦合系数K12和K23仿真模型

从上面的滤波器初始数据可以看出，K12＝K56，K23＝K45，所以需要仿真的耦合系数包括K12，K23，K34。仿真使用的模型如图7所示。因为使用的单腔参数为20mm×18mm×40mm，所以耦合系数K34的仿真模型和上面使用的模型不同，考虑到耦合的方向不同，所以使用的仿真模型如图8所示。

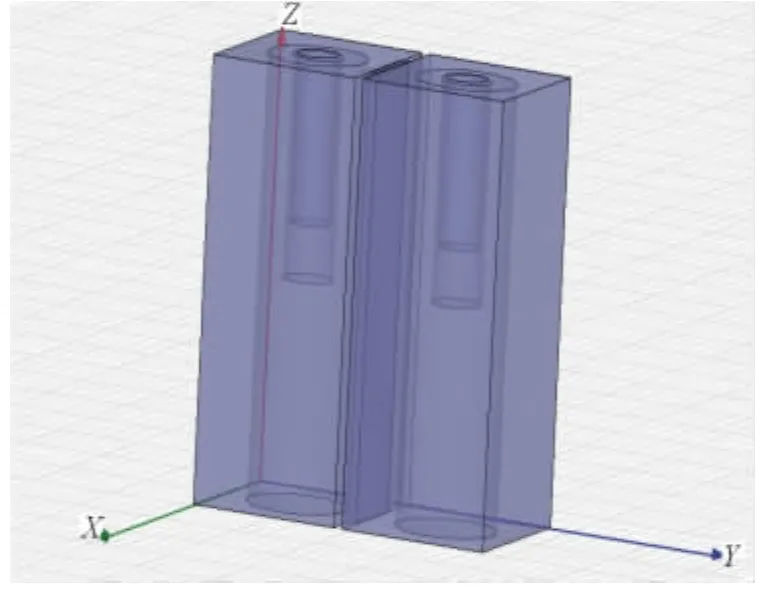
图8 耦合系数K34仿真模型

通过仿真可以看到：由K12＝K56＝0.056 18，可以得出1腔和2腔间的耦合缝隙宽度等于5腔和6腔间的耦合缝隙宽度，即w12＝w56＝11.7mm；同理由耦合系数K23＝K45＝0.042 34，可以得出w23＝w45＝9.5mm。

通过仿真可以看到：由耦合系数K34＝0.040 73，从而可以得出w34＝42.6mm。抽头结构的仿真使用图9所示的仿真模型，通过2.2节可以得到第一谐振器的群时延14.872 8ns，所以对抽头的高度进行调整，最后得到抽头高度为15mm。

2.4 整体仿真

使用上面仿真得到的数据进行整体建模，模型如图10所示。

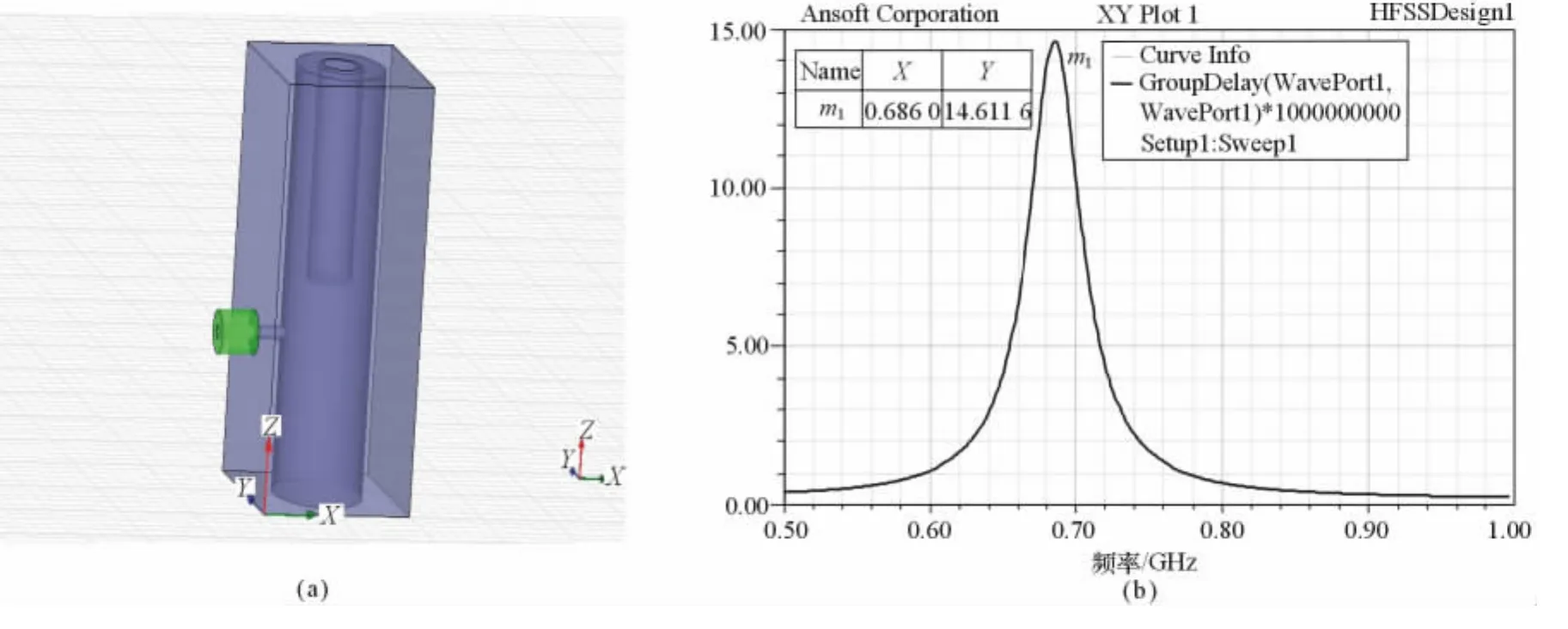
图9 抽头仿真模型

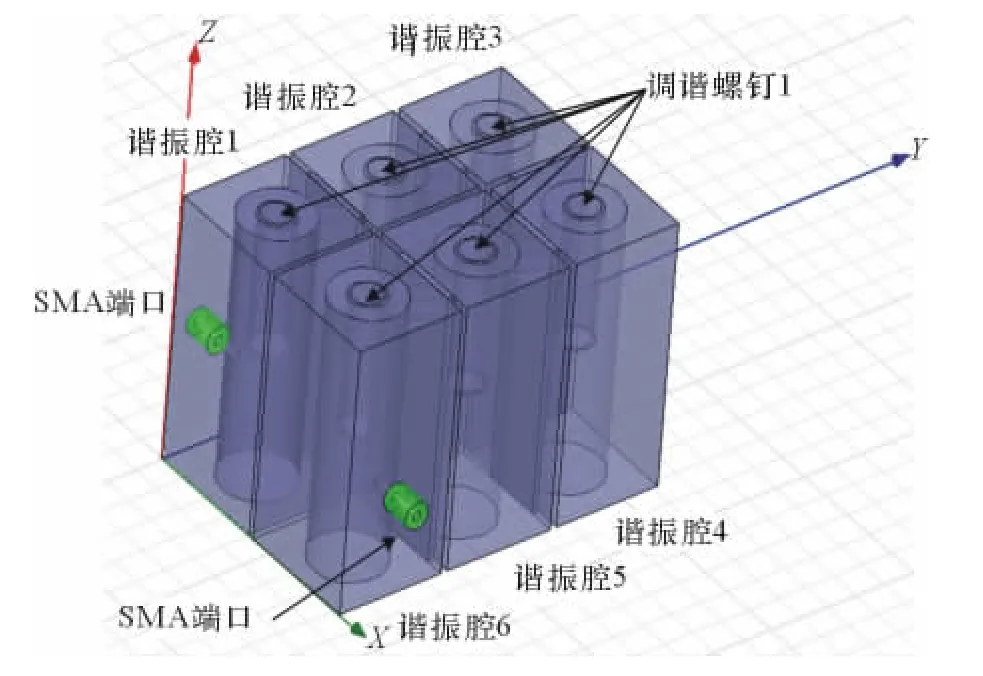
图10 滤波器仿真结构

将三维电磁仿真软件（HFSS）仿真的S8P文件导出，在ADS中建立如图11所示的电路结构图，在图中的SnP空间中导入S8P文件。将谐振腔中的电容加载效应使用6个集总电容代替，进行优化，得到滤波器的曲线如图12所示。在HFSS中得到的滤波器的主要物理尺寸如表4所示。

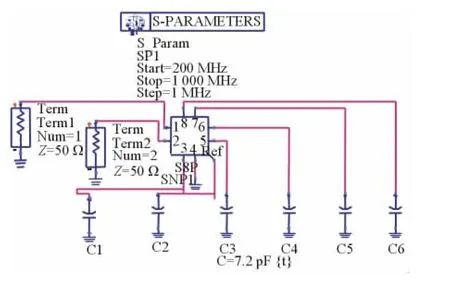
图11 ADS仿真原理

图12 ADS仿真结果

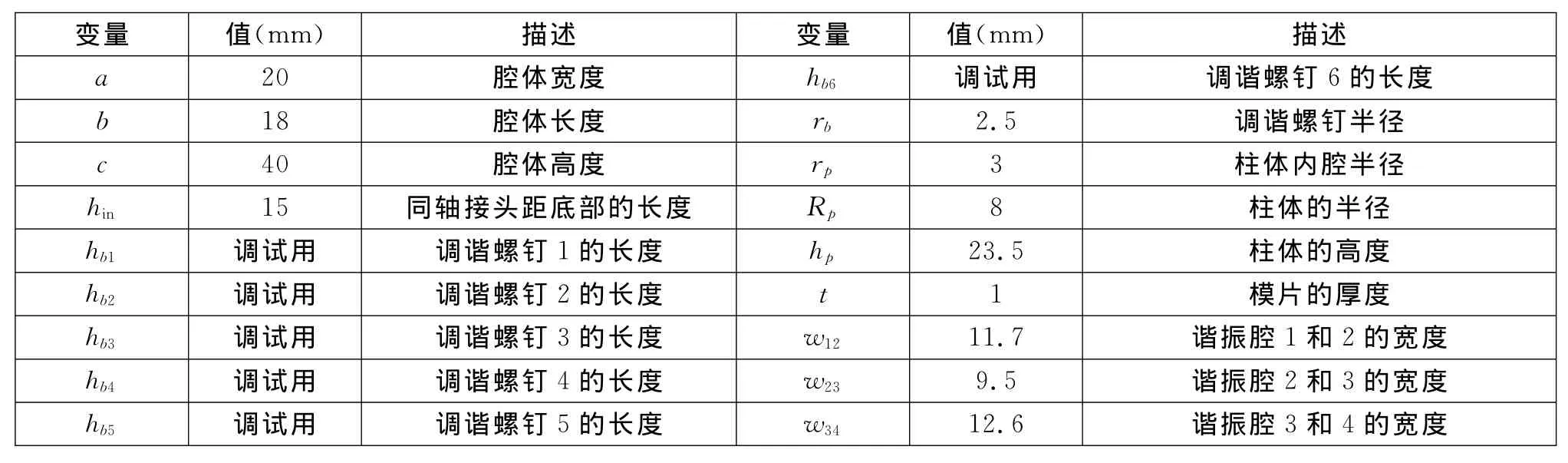
表4 滤波器主要尺寸

2.5 验证

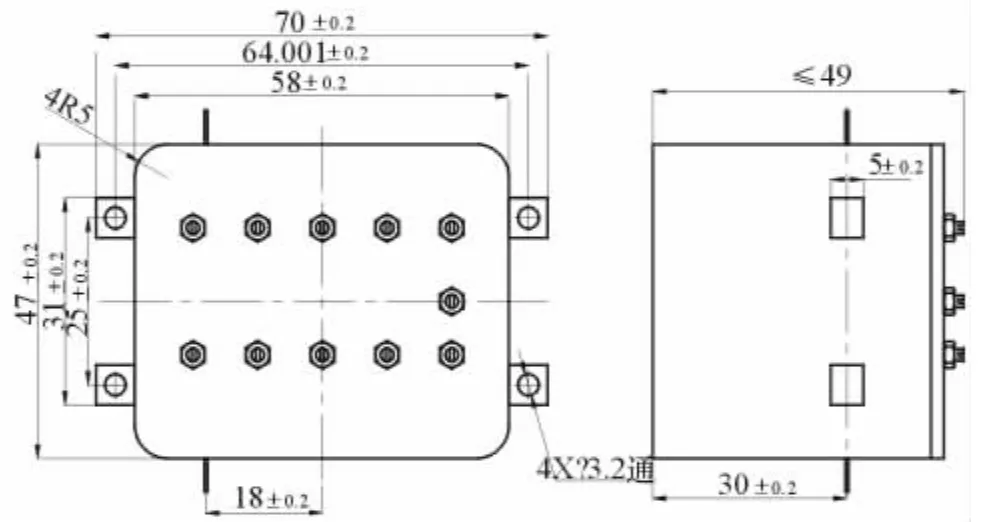
图13 滤波器外形图

考虑到腔体滤波器长度要尽量小，且采用折叠的结构形式，如图13所示。经过调试后进行实物测试，得到滤波器的测试曲线如图14所示，可以看出滤波器满足设计要求。带内插入损耗为0.8dB，回波损耗小于18dB。

3 结束语

本文提出了利用电路仿真软件和3DEM（HFSS）进行联合仿真同轴腔体滤波器的方法和步骤，然后通过一个六腔滤波器的设计具体说明了该设计方法。通过加工测试，可以得到设计的滤波器实测数据和设计要求比较吻合，这证明了该方法的有效性。

图14 测试曲线

同时使用该方法可以大大提高仿真同轴腔体滤波器的速度，缩短研制周期，对滤波器的制作和设计具有很大的实用意义。

［1］Hunter C，Billonet L，Jarry B.Microwave filter applications and technology［J］.IEEE MTT－S International，2002，50（3）：794－805.

［2］Levy B.Theory of direct－coupled cavity filters［J］.IEEE Transactions on MTT，1967，15（2）：340－348

［3］甘本祓，吴万春.现代微波滤波器的结构与设计［M］.北京：科学出版社，1973.

［4］郭硕鸿.电动力学［M］.北京：高等教育出版社，1997.