子阵级阵列加权置零综合技术研究

黄 华，林桂道，张 行

（船舶重工集团公司723所，扬州225001）

0 引 言

在日益复杂的战场环境中，雷达受到了多重干扰，这将导致探测结果的错误，因此需在天线方向图中设置一个或多个零点以对抗干扰。现在比较青睐的处理方法是自适应波束形成［1］，通过对探测的回波信号进行快拍，对采样的协方差矩阵求逆而将干扰消除。但是对于复杂作战环境下资源竞争激烈的情况，波束切换时间通常为微秒级，而在自适应波束形成中利用协方差求逆的方法其反应时间满足不了要求。因此，必须事先算好干扰方向置零的权值［2－4］，然后再增加到波束形成中。而干扰方向则通过雷达侦察设备的测向得到。

对于大型的相控阵天线，为了降低馈电网络的复杂性及研制成本，实际操作过程中通常采用子阵技术。本文将在子阵级阵列的条件下给出置零解析方法的详细推导过程，分别从这3个方面予以加权：（1）复数加权，即单元幅度和相位都进行调整；（2）仅幅度加权，只调整单元的幅度；（3）仅相位加权，只调整单元的相位。

1 模型建立

假设子阵是均匀子阵，即每个子阵含有相同的阵元数目，且每个阵元的阵元间距是相等的，式（1）给出了采用子阵形式的波束方向图表达式，与之相对应的阵列布置如图1所示。

式中：bm为第m个子阵的幅度加权系数；M为子阵数目；amn为第m个子阵中的第n个阵元的加权系数；N为每个子阵中的阵元数目；k＝2π／λ为波数，λ为波长；θ为来波与阵列法线方向的夹角；φmn为第m个子阵中的第n个阵元的初始相位；dmn为第m个子阵中的第n个阵元到相位中心的距离，dmn＝［（m－1）N＋n］×d。

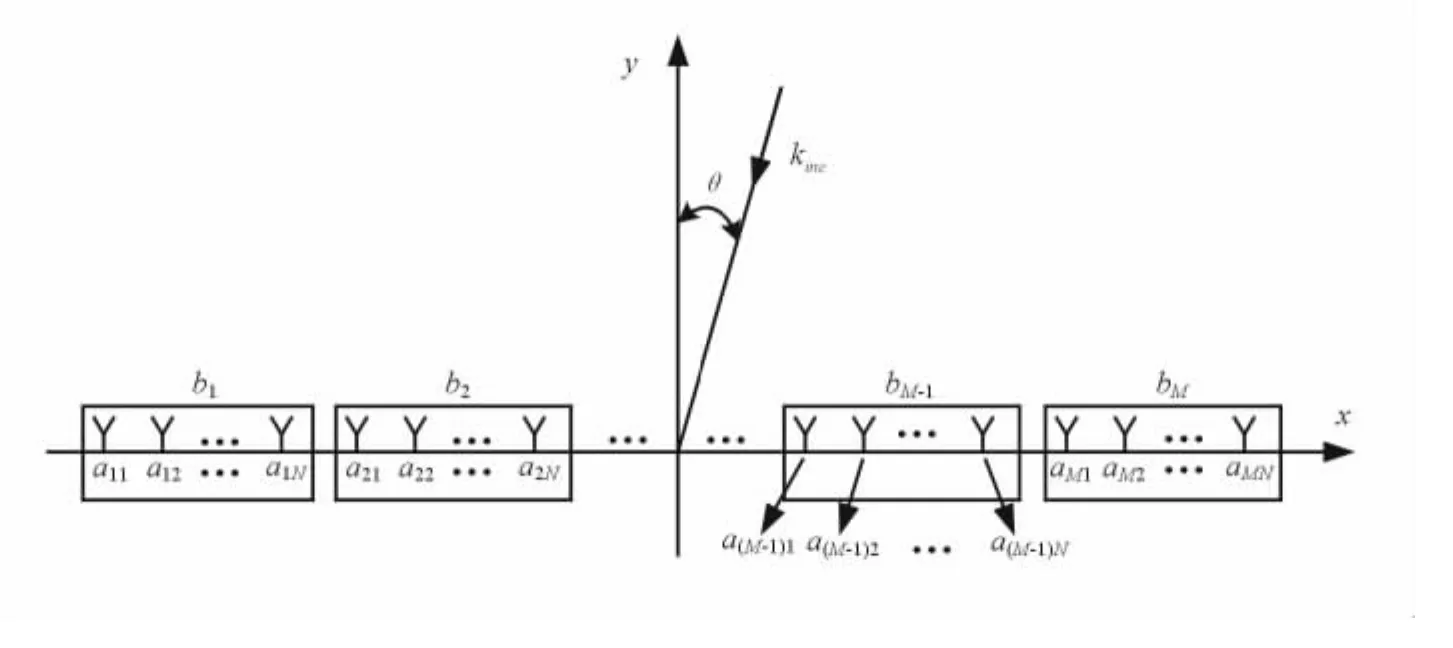
图1 具有子阵的阵列布置图

2 公式推导

设干扰方向为θp，在此干扰方向下，阵列天线的方向图满足下列方程：

那么，置零操作就转换成解一线性方程组。实际操作过程中每个子阵内单元的加权系数amn是不可改变的，可调整的系数只可能是子阵的权系数bm。令初始子阵系数b0m＝x0mejy0m，其中y0m＝0；扰动量为ωm＝xmejym，将此量代入式（2），并将其实部和虚部进行分离可得：

式（3）是关于xm和ym的非线性方程组，因此，需将其转换成线性方程组，采用Taylor级数展开式在b0m处展开可得：

解线性方程组（5）有多种方法，此处采用Gram－Schmidt正交化法进行求解：

（1）向量构造

构造2P个2M＋1（M为阵列中子阵总数）维列向量Xp（p＝1，2，…，2P），P为所需置零的总数。

（2）正交化

式中：‖‖表示求范数；I和Q分别为（2M＋1）×（2M＋1）的单位矩阵和正交投影矩阵。

（3）扰动向量求取

式中：W为任意（2M＋1）维非零列向量。

为了计算简单，一般取：

（4）加权权值求取

将扰动向量ω按其第2M＋1个分量进行归一化，可得：｛x1，y1，…，xm，ym，…，xM，yM，1｝，所以，最后的权值可表示为：

上述给出的推导便是复数加权置零的全部实现过程，而对于仅幅度加权和仅相位加权，只要分别令ym＝0和xm＝0即可。

3 仿真结果及分析

对于全部单元加权置零而言，3种加权置零方法的效果是相同的，本文中仅以幅度加权置零为例给予说明。

阵列共有64个单元，其中16个子阵，每个子阵包含4个单元，未置零前的权值是通过子阵和子阵内单元联合加权所得。

图2给出了在10°方向上置零操作前后的方向图对比，置零前方向图最大副瓣电平为－37.6dB，置零后方向图的最大副瓣电平为－37.1dB；置零前方向图在10°处的副瓣电平只有－44.3dB，而通过本文方法所得置零后在10°方向上的零深达到了－340.8dB。

图3给出了置零前后子阵上的电流对比，置零后的电流值仍关于中心单元对称，且电流值的扰动甚小。综合分析可知，本文置零方法所得的零深较深，且加权的电流幅值扰动很小，但是所置零点的宽度较窄：－60dB处只有0.6°，－80dB处只有0.3°，零点越深，零宽越窄。如此窄的零宽，明显不能工程实用。

鉴于以上零宽较窄的问题，可在10°的左右各置1个零点，达到加宽零点的目的。

图4给出了在9.5°、10°、10.5°3个方向同时置零操作前后的方向图对比，置零前方向图最大副瓣电平为－37.6dB，置零后方向图的最大副瓣电平为－33.2dB；置零前方向图在10°处的副瓣电平只有－44.3dB，而通过本文方法所得置零后在10°方向上的零深达到了－331.4dB。

图2 置零前后方向图对比

图3 置零前后电流分布

图5给出了置零前后子阵上的电流对比，置零后的电流值仍关于中心单元对称，与图3相比，电流值的扰动变大。所置零点的宽度明显得到改善：－60dB处达到2.8°，－80dB处达到1.4°。得以加宽的零深可用于工程实践。

4 结束语

图4 零点加宽置零前后方向图对比

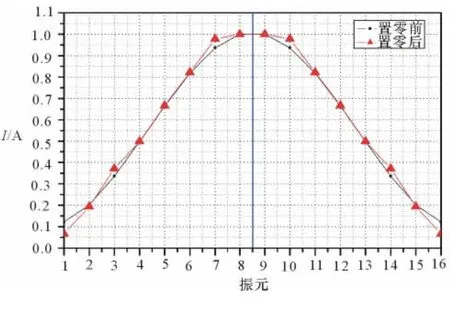
图5 零点加宽置零前后电流分布

本文首先从定义出发推导了子阵级阵列置零时所满足的线性方程组，然后采用Gram－Schmidt正交化法对其进行求解。以64个单元、16个子阵的阵列联合加权为例，在10°方向上分析了单点置零和邻近三点置零，第二种操作下方向图的最大副瓣电平虽有4dB的变化，但仍有－33.2dB，最关键的是零点的宽度较宽，能用于工程实践。

［1］曹运合，张焕疑，张守宏，等.宽度相控阵雷达数字波束形成与干扰置零方法［J］.电子与信息学报，2007，29（2）：365－369.

［2］Mayhan J T，Simmons A J.Wideband adaptive antenna nulling using tapped delay lines［J］.IEEE Transactions on Antenna and Propagation，1981，29（6）：923－936.

［3］武思军，张锦中，张曙.阵列波束的零陷加宽算法研究［J］.哈尔滨工程大学学报，2004，25（5）：658－661.

［4］虞舟凯，杨莘元.零陷展宽算法的性能研究［J］.应用科技，2006，33（3）：1－3.