工件台方镜轻量化结构的拓扑优化设计

刘 育，胡 月，吴 飞

(上海微电子装备有限公司，上海 201203)

光刻技术在经历了接触式-接近式-扫描投影式-分步重复式的几个重大技术发展阶段后，目前已转向步进扫描式光刻机的研究[1]。光刻机超精密工件台是光刻机的核心单元之一，其运动精度直接影响光刻机的分辨率，速度和加速度直接影响光刻机的产率[2～4]。随着MEMS技术的发展，精密工件台应用范围越来越广，定位精度及速度要求越来越高[5]。方镜作为工件台的核心零件，承载着硅片，同时安装了标记及能量测量传感器、零位传感器、垂向测量传感器以及干涉仪反射镜（包括平面镜和45°棱镜）。方镜的高模态为工件台的控制精度提供有力保障，方镜的轻量化为工件台的高加速度及高速度提供支持。为此，开展对方镜的轻量化研究具有重要意义。

结构拓扑优化在工程结构设计的初始阶段为设计者提供一个概念性设计，使结构在布局上采用最优方案，与截面优化和形状优化相比能取得更大的经济效益，已经在汽车、精密加工设备以及微机构等领域广泛研究及应用[6～8]。其主要思想是把寻求结构的最优拓扑问题转化为在给定的设计区域内寻求材料的最佳分布问题，探讨结构构件的相互联结拓扑形式，使结构能在满足有关响应等约束条件下使结构的某种性能指标达到最优。

本文从材料的选择以及背面的轻量化形式完成方镜轻量化的最佳拓扑结构形式，克服了传统参数化设计的局限性。

1 方镜材料选择

对于工件台的方镜来说，其模态及轻量化要求非常高，同时在空间应用中，方镜所受的热载荷是受内部及外部热流的影响而不断变化的，因此对于热特性的要求较高。堇青石陶瓷作为新型的加工材料，由于其优异的结构、力学性能，得到广泛的应用。从表1中可以看出堇青石陶瓷材料具有较高比刚度，较好的热稳定性，与其他常用材料相比具有明显的优势。经过综合考虑，本文中方镜的材料选用堇青石陶瓷。

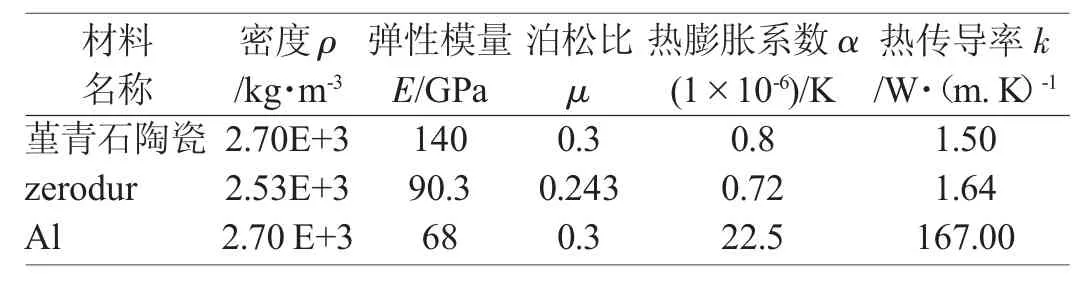
表1 常用方镜材料的性能

2 拓扑优化理论基础

2.1 基本理论

拓扑优化是一种数学方法，能在给定的空间结构中生成优化的形状及材料分布，其目的在于用最少的材料得到结构的最佳性能。常见的连续体拓扑结构优化方法主要有均匀化法、变厚度法和变密度法。变密度法是一种比较流行的力学建模方式，与采用尺寸变量相比，它更能反映拓扑优化的本质特征。所以本文采用变密度法进行优化。

变密度法是连续体拓扑优化的常用方法，属于材料描述方式。该方法的基本思想是引入一种假想的密度，即0-1的可变材料，指定每个有限单元的密度相同，并以每个单元的相对密度为设计变量，这样结构拓扑优化问题被转换为材料的最优分布问题。当单元相对密度z=0时，表示该单元无材料，单元应删除；当单元相对密度z=1时，表示该单元有材料，应保留或增加该单元。其中应用得比较多的模型是SIMP(Solid Isotropic Microstructure with Penalization)法，其材料模型为：

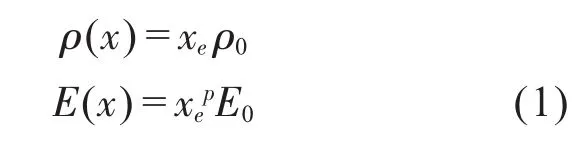
式中：xe为每个单元的相对密度，ρ(x)为拓扑优化设计变量，ρ0为设计区域每个单元的固有密度，E(x)为优化后的弹性模量，E0为初始弹性模量，p为惩罚因子[9]。

2.2 拓扑优化的SIMP模型

拓扑优化的SIMP方法假设材料密度在单元内是常数并以其为设计变量，而材料特性用单元密度的指数函数来模拟。相对密度的指数函数关系，简化了计算求解过程，优化过程中以单元设计变量的大小决定单元取舍，在消除棋盘格现象和数值稳定性方面有了很大的提高。结构设计中经常以刚度最大化或应变能最小作为优化的目标函数，以结构整体的体积约束为优化的约束条件，可以转化为给定结构刚度约束下以体积最小为目标函数，基于SIMP方法的连续体结构拓扑优化模型为：

式中，目标函数定义为结构总体积V，Vj为优化后的单元体积，x为设计变量，xj为单元设计变量，C(x)为结构的总体柔度，C*为结构的总体柔度约束，U为位移列阵，K为结构总体刚度矩阵，F为力向量，xmin为单元设计变量下限（引入密度xmin的目的是防止单元刚度矩阵奇异）。p为惩罚因子，n为结构离散单元总数。

3 方镜拓扑优化模型求解

3.1 方镜模型

工件台的方镜轻量化前的实体模型如图1，外形几何参数及质量如表2，材料为堇青石陶瓷。

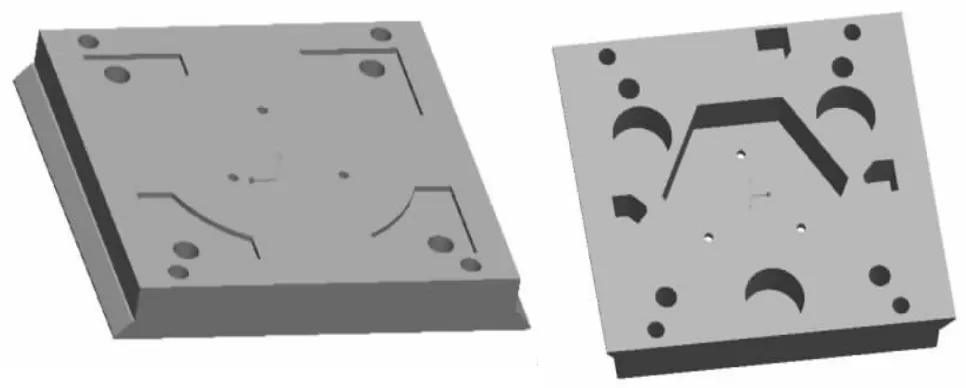
图1 方镜实体模型

表2 实体方镜外形几何参数及质量

方镜有限元模型如图2及图3所示，方镜正面包括2个干涉仪放射镜、4个零位传感器及4个测量传感器接口。背面包括平面矢量电机接口、3个重力补偿器及3个垂向测量传感器接口。定义垂向方向为方镜正面上表面的法向。

图3 方镜有限元模型（背面）

在工作工况时，方镜采用背面三点支撑，由背面的3个重力补偿器支撑提供支撑及约束（单个约束10 000 N/mm）。

本次拓扑优化主要针对背面，模型设计区域和非设计区域定义情况如图3所示，设计区域为方镜背面，同时为保证方镜的整体性及平面矢量电机接口具有一定的壁厚，所以将方镜外形四周（厚5 mm）及正面（厚8 mm），以及平面矢量电机接口四周（厚5 mm）等区域排除在设计区域以外。

方镜拓扑优化以最小化结构体积（质量）为目标，结构第1阶固有频率700 Hz为约束条件。

3.2 拓扑优化及应用

采用OptiStruct优化软件，对方镜进行连续体拓扑优化，流程如图4所示。经过迭代分析计算，得到了方镜最终拓扑结构形式。优化后的轻量化结构形式如图5所示，拓扑优化得到的轻量化结构形式制造加工工艺性较差，并不能直接应用于工程，需要根据要求将轻量化结构形式转换为符合制造加工工艺性的加强筋结构形式，最终模型如图6所示。

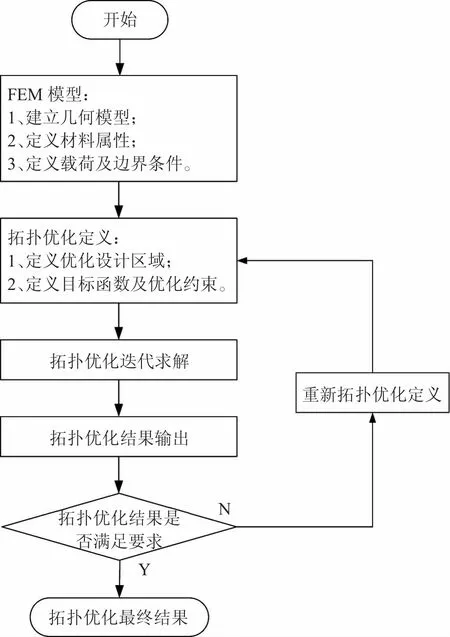
图4 拓扑优化流程图

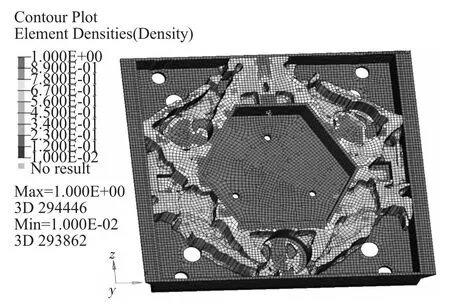
图5 拓扑优化结果

3.3 优化结果及对比

为对比优化结果的模态和轻量化，将方镜拓扑优化后的最终模型与常规结构的初始模型（图7）进行仿真分析比较。常规结构的初始模型采用了三角形轻量化孔，较正方形等轻量化孔的刚度要好，同时也能达到相当高的轻量化率。

图6 拓扑优化后的最终模型

图7 常规结构的初始模型

在工作工况时，方镜背面的3个重力补偿器约束（单个约束10 000 N/mm）下，对两模型进行对比仿真计算得到结构第1阶模态振型图，如图8及图9所示。

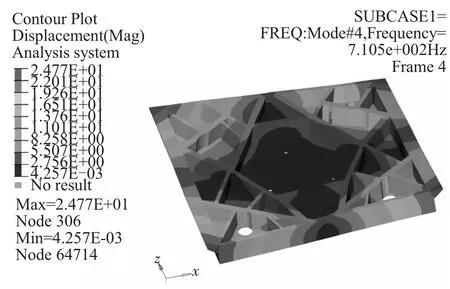
图8 拓扑优化后最终模型的结构第1阶模态振型图

拓扑优化方式和常规结构方式的方镜模型的结构第1阶模态和轻量化率的对比结果列于表3。由表中可看出，拓扑优化方式与常规结构方式相比，结构第1阶模态优化后为710.5 Hz，提高+4.5%。同时，在轻量化率上也有优势，提高+8.2%。因此，拓扑优化的结果要优于常规结构方式。

图9 常规结构初始模型的结构第1阶模态振型图

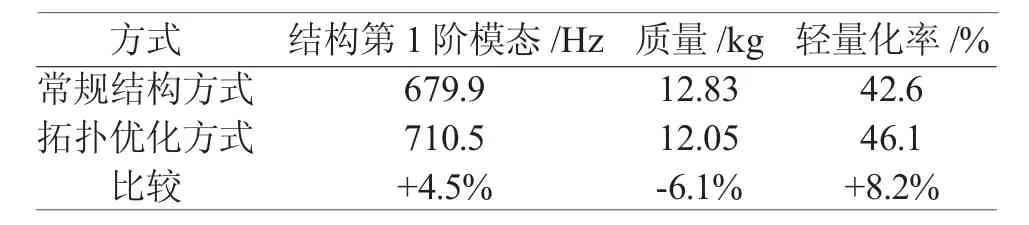
表3 拓扑优化与常规结构方式的结果对比

4 结 论

方镜结构设计是工件台研制过程中的关键技术之一。为提高方镜的结构模态，最大限度的降低方镜质量，应当在设计过程中充分考虑其材料的选择以及轻量化结构形式的选择。本文重点对方镜背面轻量化形式进行了拓扑优化，并进行设计与分析。分析结果表明：拓扑优化后的方镜在提高结构模态的同时，又保证了很高的轻量化率，体现出了拓扑优化作为科学的指导方法，在工件台结构设计过程中具有重要的实际应用价值。

[1] 彭祎帆，袁波，曹向群.光刻机技术现状及发展趋势[J].光学仪器，2010，32（4）：80-85．

[2] 姚汉民，胡松，邢廷文.光学投影曝光微纳加工技术[M].北京：北京工业大学出版社，2006：130-135．

[3] 邓习树，吴运新，杨辅强，等.用于光刻机模拟运动的精密工件台宏动定位系统研制[J].电子工业专用设备，2007，36(2)：39-43．

[4] 袁琼雁，王向朝.国际主流光刻机研发的最新进展[J].激光与光电子学进展，2007，44(1)：57-64.

[5] 宋文荣，于国飞，王延风，等.六维磁悬浮纳米级精密工件台的研究[J].微细加工技术，2003，(1)：15-21．

[6] 潘锋，朱平，孟瑾.微型货车车架的拓扑优化设计[J].机械设计与研究，2008，24(2)：87-90．

[7] 饶柳生，侯亮，潘勇军.基于拓扑优化的机床立柱筋板改进[J].机械设计与研究，2010，26(1)：87-92．

[8] 褚金奎，郝秀春，王立鼎.拓扑优化方法的研究现状及在微机构设计中的应用[J].微纳电子技术，2003，(8)：87-91．

[9] 彭禹，郝志勇.基于动力学仿真的零件拓扑优化方法研究[J].中国机械工程，2007，18(8)：975-978．