LED显示屏色域边界的快速计算

宋 超，王瑞光，陈 宇，邓意成，2

(1.中国科学院长春光学精密机械与物理研究所，吉林长春 130033;2.中国科学院大学，北京 100049)

1 引 言

LED(Light Emitting Diode)显示屏作为一种显示设备，具有色域广、显示面积大和使用寿命长等优点，被广泛应用于标识、广告和娱乐等场所[1]。LED显示屏的色域是指显示屏本身能够表现的最大颜色范围，通常用均匀颜色空间如CIELAB[2-3]中的有界体积表示。在实际应用中，为了更好地发挥LED显示屏色域范围大的优势，常常需要对其色域进行分析或者与其他显示设备进行不同色域间的映射。无论色域分析还是色域映射，色域边界计算都起着重要的基础作用，其计算速度和精度直接影响着色域应用的效率和准确性。

目前广泛采用的色域边界求解算法是首先对色域边界进行采样，然后利用插值计算或拟合等方法计算出所求色域边界上其他的边界点数据，从而完成对色域边界的描述[4]。如国际照明委员会(CIE)推荐的局部最大值色域边界描述(SMGBD)算法，首先将色域边界在球坐标系中分块，并取每块中采样数据的最大值，然后对这些最大值对应的采样点进行三角化来描述色域边界[5-6];Xu等引入的色域球概念，通过对插值三角形进行预查找来提高色域边界整体求解速度[7];Wang等提出的将小样本测量和样条插值相结合的色域边界算法，能够减少采样数据存储量[8]。上述文献中，都是通过实际测量获得离散数据和进行插值运算相结合的方法来计算色域边界，需消耗大量的存储空间和运算时间，不利于在实际应用中快速准确地得出计算结果。

本文针对上述算法中的不足，提出了一种求解LED显示屏色域边界的快速迭代算法。本算法不需要存储大量的采样点数据和进行复杂的插值运算，充分利用了LED显示屏的特征矩阵，可快速计算出映射线与色域边界交点进而拟合出各个等色相面内的色域边界，在实际应用中能够满足对LED显示屏进行色域分析和色域映射的要求。

2 色域边界计算

2.1 确定颜色与色域的关系

本文算法在迭代计算过程中，需重复确定颜色与LED显示屏色域的关系，即确定颜色在LED显示屏色域内还是色域外。根据LED显示的色度学原理，利用LED显示屏特征矩阵和CIELAB颜色空间到RGB设备空间的反向转换运算，给出了颜色是否在LED显示屏色域内的判断方法。

CIELAB颜色空间作为一种视觉均匀的颜色空间，在工业领域得到了广泛应用。色域边界描述和色域映射相关算法多在CIELAB颜色空间中进行阐述和评价[9]。本文提出的迭代算法同样选择了CIELAB颜色空间及其色差公式来计算LED显示屏色域边界。

根据LED显示原理可知，LED显示屏是一种采用红、绿、蓝三原色加色法混色的显示设备。若某颜色在LED显示屏色域内，则该颜色的三原色标量(归一化亮度，指相应原色LED的亮度与LED显示控制系统能够表现的最大亮度的比值)均应分布在[0，1]区间内;反之，若该颜色在LED显示屏色域外，则其三原色标量中至少有一个分布在[0，1]区间外。通过分析三原色标量值，即可明确某种颜色在LED显示屏的色域内还是色域外。

为了计算某颜色的三原色标量，首先需将该颜色从CIELAB颜色空间转换到CIE 1931 XYZ颜色空间下，得到该颜色的三刺激值，变换公式如式(1)所示。

其中:

式中，L*、a*、b*为该颜色在CIELAB颜色空间中的坐标值;Xn、Yn、Zn为参照白点的归一化三刺激值，X、Y、Z为该颜色的三刺激值。

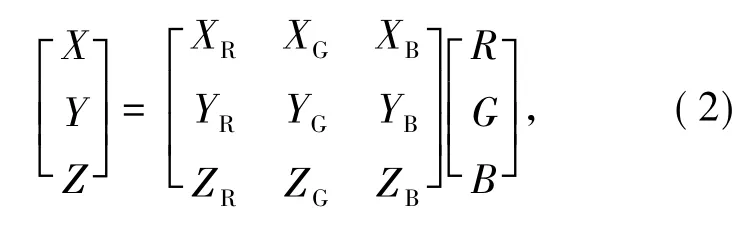
LED显示屏红绿蓝三原色LED点亮时，其配光色的三刺激值与三原色标量之间可进行线性变换，变换公式如式(2)所示。式中，R、G、B 为三原色标量，R∈[0，1]，G∈[0，1]，B∈[0，1];XR、YR、ZR、XG、YG、ZG、XB、YB、ZB分别表示红、绿、蓝LED最大亮度时的三刺激值，其组成的3×3矩阵称为LED显示屏的特征矩阵，反应了颜色三刺激值和三原色标量的线性关系。

由三原色LED三刺激值的非线性分布可知，LED显示屏特征矩阵必然存在逆矩阵。对公式(2)进行逆变换运算，可由该颜色的三刺激值得其三原色标量R、G、B。分析三原色标量的取值，即可在CIELAB颜色空间中确定该颜色与LED显示屏色域的关系。

2.2 色域边界计算原理

在CIELAB颜色空间中，首先以所描述的LED显示屏色域中心E为圆心，令色相角为α、映射线与明度轴正方向的夹角为θ、色域边界到圆心的长度为半径r，建立色域球坐标系如图1所示，其中 α∈[0°，360°]，θ∈[0°，180°]。

图1 色域球坐标系Fig.1 Spherical coordinates for color gamut

LED显示屏色域中心一般距离L*a*b*坐标为(50，0，0)的点较近，同时为了便于计算，本文中选此点为 E点，即令=50=0，=0。LED显示屏在CIELAB颜色空间中的色域模型及色域E点相对位置关系如图2所示。

图2 LED显示屏在CIELAB颜色空间中的色域模型Fig.2 LED display panel gamut model in the CIELAB color space

色域球坐标系与标准CIELAB空间的转换如式(3)所示。色域球坐标系与标准CIELAB空间的转换如式(3)所示。

基于色域球坐标系，在LED显示屏色域的等色相面内，对θ等角度差取值，计算每条由E点射出的映射线与色域边界的交点并进行拟合，即可得该色相面的色域边界。等色相面内映射线与色域边界交点求解原理如图3所示，其中横坐标为彩度，纵坐标为明度。

图3 色域边界确定方法Fig.3 Method for determination of gamut boundary

图3中，在第k次迭代时，需首先确定映射线上包含交点的线段mknk，取其中点pk，计算pk点到E点的距离rpk:

式中，rmk、rnk分别是 mk、nk到 E 点的距离。若 pk在LED显示屏色域内，令rmk+1=rpk，rnk+1=rnk;反之，若pk在LED显示屏色域外，则令rmk+1=rmk，rnk+1=rpk。取线段mk+1nk+1中点pk+1，重复迭代计算，直到色域边界精度满足要求。最后一次迭代所得线段的中点即为该映射线方向上的LED显示屏色域边界。

2.3 确定迭代初始值

利用提出的迭代算法计算映射线与色域边界的交点，关键是要确定迭代初始值，即确定第一次迭代时rn1的值(rm1=0)。本文根据LED显示屏颜色三刺激值与三原色标量的线性关系及CIE 1931 XYZ颜色空间到CIELAB颜色空间的变换公式，并考虑到对不同LED显示屏的色域边界进行色差分析的需要，提出了一个常数rn1的计算方法。

根据公式(2)，当 R、G、B 分别在[0，1]区间内取值时，X、Y、Z 的取值范围分别是[0，XR+XG+XB]、[0，YR+YG+YB]和[0，ZR+ZG+ZB]。本文在CIELAB颜色空间中进行颜色计算时以D65为参考，即对LED显示屏按色温6 500 K白平衡处理，并对白场三刺激值归一化，即令X、Y、Z的取值范围分别为[0，Xn]、[0，Yn]和[0，Zn]。

分析CIE 1931 XYZ颜色空间到CIELAB颜色空间的变换公式(5)可知，f(t)函数在[0，+∞]内为正数且单调递增，L*≥0且 L*在Y=Yn时取最大值=100;当X=Xn且Y=0时或当X=0且Y=Yn时，可得a*绝对值的最大值同理，可得b*绝对值的最大值

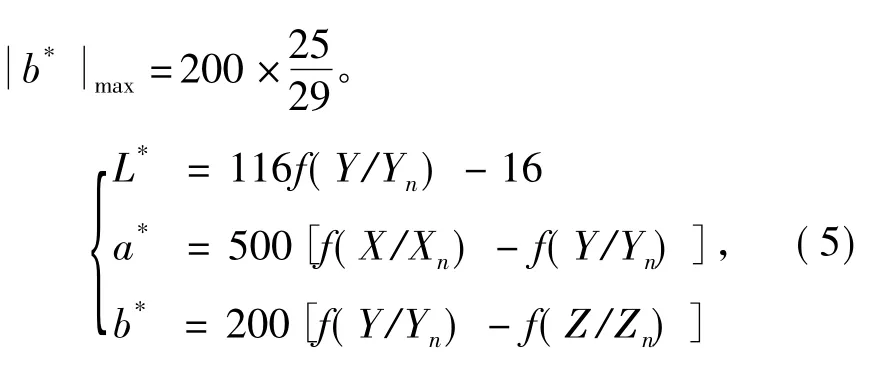
图4 长方体在第一象限中的部分Fig.4 Part of the cuboid in the first quadrant

由上述分析可得出rn1:

当 R、G、B 分别在[0，1]区间内取值时，红绿蓝LED点亮时配光色对应的CIELAB颜色坐标L*、a*、b*的绝对值不可能同时达到相应的，所以在球坐标系中到E点距离为rn1的点必然不在LED显示屏的色域内，因此由式(6)计算得到的rn1可以作为本文算法的迭代初始值;同时，rn1为常数，对不同的LED显示屏色域边界迭代求解时，经过相同的迭代次数可得到相同的最大色差值，获得相同的色差精度，有利于对不同的LED显示屏进行准确的色域分析和色域映射。

3 实验结果及分析

3.1 实验准备

对LED显示屏在CIELAB均匀颜色空间中进行色域边界的拟合实验。首先选择长春希达公司点间距为3 mm的集成3合1全彩LED显示屏，对其进行色度优化校正及白平衡处理，使白场色温达到6 500 K左右。处理后测得三原色及白场的最大亮度及色品坐标值见表1。根据亮度值和色品坐标坐标值计算归一化三原色及白场的三刺激值如表2所示。根据公式(6)计算得出的迭代初始值见表3。

表1 处理后三原色及白场最大亮度及色品坐标Table 1 Maximum brightness and chromaticity coordinates of three primary colors and white field after processing

表2 归一化三原色及白场三刺激值Table 2 Tri-stimulus values of normalized three primary colors and white field

表3 迭代初始值Table 3 Iteration initial values

3.2 计算精度分析

迭代算法与迭代次数有关。由公式(6)和CIELAB颜色空间中2个颜色的色差计算公式(7)可知，k次迭代后，映射线与色域边界交点的真实值与计算值色差取值范围可由式(8)表示。

求解的色域边界最大色差值与迭代次数k的关系如图5所示。横坐标为迭代次数，纵坐标为映射线与色域边界交点计算值与真实值之间的最大色差值。由图可知，随着迭代次数的增加，最大色差值以2－1倍的速度迅速减小。

图5 色域边界点最大色差与迭代次数的关系Fig.5 Relationship between maximum color difference of gamut boundary points and iteration times

通过比较LED显示屏色域边界点的采样值和计算值，可以证明边界点的真实值与计算值色差满足公式(8)。根据文献[10]可知，LED显示屏三原色标量R、G、B在RGB设备空间中为立方体，其外表面对应CIELAB颜色空间中显示屏色域的边界面。在RGB设备空间中对R、G、B等间距各9点取值，得到386组立方体表面组合值。测量各配色的 CIELAB色度值L*、a*、b*，由式(3)可得对应映射线的α和θ值及边界点的真实值。由各映射线的α和θ值，进行11次迭代计算，可得映射线与色域边界交点的计算值。比较386组边界点真实值和计算值的色差值，得到色差最大值、最小值和平均值及对应的边界点真实值和计算值如表4所示。

由表4和公式(8)可知，11次迭代计算后，每条映射线上的色域边界点真实值和计算值色差都在[0，0.23]范围内，验证了本文算法的精确性。

表4 边界点真实值与计算值比较Table 4 Comparison of real and calculated values for boundary points

3.3 计算速度分析

综合本文中映射线与色域边界交点坐标迭代计算过程，给出迭代计算步骤如下:

(1)根据式(4)，由 rmk和 rnk计算 rpk。

(2)根据式(3)，计算pk点对应的CIELAB颜色空间坐标

根据上述迭代计算步骤中各个公式可计算出，每次迭代最多需要进行约31次乘法运算和13次加法运算。通常11次迭代即可满足较高的精度，使用2 GHz主频的计算机，Matlab编程计算180个映射线交点，耗时仅0.25 s左右，相比文献[5]中的插值算法至少3 s的计算时间，计算速度提高近15倍。

应用表2和表3的数据，在色相角为30°的等色相面内，每隔1°取一条由E点射出的映射线，对LED显示屏的色域边界进行拟合。图5为使用文中提供的算法进行11次迭代后的拟合效果。

图6中，横坐标为彩度，纵坐标为明度。从图6可以看出，11次迭代的拟合边界已经非常平滑，仅在低彩度时有轻微的波动，在中高彩度以及转折角附近拟合结果非常理想。为提高低彩度时色域边界的平滑度，可适当增加低彩度区域对应映射线与色域边界交点求解迭代次数。

图6 30°色相角时LED显示屏的色域边界Fig.6 Gamut boundary of LED display panel under 30°hue angle

图7 LED显示屏的色域边界Fig.7 Gamut boundary of LED display panel

对色相角α每隔12°取一个色相面，在等色相面内每隔1°取一条由E点射出的映射线，对整个LED显示屏色域边界进行拟合。图7为11次迭代后的拟合效果。

4 结 论

本文提出的LED显示屏色域边界算法可计算任意映射线与色域边界的交点进而拟合出每个等色相面内的色域边界，计算原理简单，方法可靠，不需要存储大量的离散采样数据和进行复杂的插值运算。采用11次迭代时，每条映射线上的色域边界点真实值和计算值最大色差仅有0.23，与文献[7]中386次采样点的色差仅达到0.4 ～2.31 相比，最大色差降低了2.08。经实验验证，通常11次迭代即可满足较高的精度要求，而其总计算量仅为约341次乘法运算和143次加法运算。使用2 GHz主频的计算机计算180个映射线交点，耗时仅0.25 s左右。与文献[5]相比，速度提高了近15倍。本文算法不仅适用于LED显示屏，也可用于CRT(Cathode-ray tube)显示器等可用特征矩阵表征颜色三刺激值与三原色标量关系的显示设备[11]。

[1]Chang F，Sun Z Y，Wang R G，et al.Improvement of non-uniformity correction of LED display images[J].Opt.Precision Eng.(光学 精密工程)，2011，19(4):929-937(in Chinese).

[2]Wang Y F，Zeng P，Wang Y，et al.Multi-channel printer characterization based on gamut partition[J].Acta Electronica Sinica(电子学报)，2010，38(3):507-511(in Chinese).

[3]Luo X M，Zeng P，Wang Y，et al.Color management using a hue-constancy color space[J].Acta Electronica Sinica(电子学报)，2010，38(11):2660-2668(in Chinese).

[4]Bakke A M，Farup I，Hardeberg J Y.Evaluation of algorithms for the determination of color gamut boundaries[J].J.Imag.Sci.Technol.，2010，54(5):50502-1-11.

[5]Morovic J，Luo M R.Calculating medium and image gamut boundaries for gamut mapping[J].Col.Res.Appl.，2000，25(6):394-401.

[6]Wang L.Design and application of intelligent led information display screen[J].Chin.J.Liq.Cryst.Disp.(液晶与显示)，2011，26(5):655-659(in Chinese).

[7]Xu Y F，Liu W Y.Interpolation method for calculating gamut boundaries of digital imaging output devices[J].Opt.Precision Eng.(光学 精密工程)，2006，14(2):262-265(in Chinese).

[8]Wang Y F，Liu R H，Zeng P.Extraction of printer gamut by the mixture of measurement and spline interpolation[J].J.Huangzhong Univ.Sci.Technol.(Nature Science Edition)(华中科技大学学报(自然科学版))，2007，35(7):15-17(in Chinese).

[9]Morovic J，Luo M R.The fundamentals of gamut mapping:A survey [J].J Imag.Sci.Technol.，2001，45(3):283-290.

[10]Mahy M.Calculation of color gamuts based on the neugebauer model[J].Col.Res.Appl.，1997，22(6):365-374.

[11]Zhuang S X，Qian K Y，Li X L，et al.Effect of white LEDs on Gamut of TV with direct illumination-type LED backlight[J].Chin.J.Liq.Cryst.Disp.(液晶与显示)，2011，26(4):474-479(in Chinese).