亚波长金属光栅结构的制备与矢量衍射理论分析
郑改革,詹 煜,曹 焜,徐林华
(南京信息大学物理与光电工程学院,江苏南京 210044)
1 引 言
随着光栅电磁理论研究的不断深入和微加工技术的不断进步,研究人员逐渐发现亚波长金属光栅表现出了很多奇异的光学现象,比如介质层上的亚波长金属光栅产生的表面等离子体(Surface Plasmon)可以极大地增强光栅下介质层内的透射光强[1-3],亚波长金属光栅能够同时实现TE偏振(电矢量平行于光栅刻槽)的高反射和TM偏振(电矢量垂直于光栅刻槽)的高透射[3]等。目前,光栅的标量衍射理论已较为成熟,但它只适用于表面结构特征尺寸远大于入射波长的光学元件。当光学元件的特征尺寸小至波长或亚波长量级时,基于标量衍射理论的框架进行二元光学器件的设计将缺乏可靠性,而需要采用电磁矢量衍射理论来分析研究光栅的衍射特性。
亚波长金属光栅是一种特殊的光栅类型,而高深宽比(High Aspect Ratio,HAR)结构是其中比较典型的一类,其在生物传感器、太阳能电池、超衍射光学光刻技术、近场光学成像等领域都有大量的应用[4-7]。高深宽比金属结构的加工是目前微机电系统(MEMS)研究的热点与难点之一。金属器件在耐高温、高压以及在苛刻环境下的使用比硅基器件具有明显的优势,但由于目前金属结构加工手段的欠缺,截止到目前绝大多数MEMS器件依然以硅基微加工技术为主。
本文利用纳米压印技术结合溅射和反应离子刻蚀工艺制备了深宽比达到4∶1的亚波长金属光栅,使用紫外可见近红外光谱仪测得了光栅的反射光谱。根据参考文献[8]提供的方法,在传统的严格耦合波理论的基础上,把光栅区域电磁场的空间谐波通过勒让德多项式展开,求解光波在亚波长光栅体内的场分布。比较发现,实验测量同理论分析结果在共振波长处吻合得很好。当光栅的深宽比增加时,在反射光谱中会观察到更多的谷值,我们分析了其产生的原因。
2 光栅的矢量衍射理论分析
分析如图1所示的亚波长光栅。区域1的介电常数为ε1,区域3的介电常数为 ε3,中间为介电常数受到周期性调制的光栅区。光栅平面的法线方向沿z轴,光栅矢量沿x轴。光栅周期为Λ,占空比为f,光栅深度为h。光栅区域(0<z<h)包含了两种介质的周期分布,其介电系数为一周期函数,对应的介电常数表示为ε(x+Λ)=ε(x)。

图1 亚波长金属光栅基本结构Fig.1 The basic structure of subwavelength metallic grating
严格耦合波分析(Rigorous Coupled Wave Analysis)[8-9]方法由于计算简单快捷,被广泛应用于各种周期性结构衍射体的电磁场衍射的分析中,但其没有充分考虑光栅介质以及电磁波在光栅矢量方向上的边界最佳匹配条件,在求解本征矩阵方程时,计算结果往往收敛很慢,有时甚至出现数值溢出,导致病态矩阵。这种情况对于TM波尤为突出。衍射波由传播波和倏逝波组成,对于远场衍射,倏逝波在到达远场前就已衰减为0,因此对远场衍射的贡献主要是传播波。但分析表面等离激元极其相关的亚波长光学现象时,涉及的往往都是TM波而且是近场情形,尤其是存在倏逝波的情形,所以为了更深刻的分析亚波长金属光栅的衍射特性,有必要对耦合波分析方法做一定的修正。
我们利用文献[8]的方法,在传统的严格耦合波理论的基础上,先是采用快速傅立叶因式分解(FFF)的方法求得TM偏振光入射下的耦合波方程,再把光栅区域电磁场的空间谐波通过勒让德多项式展开[10],避免了病态矩阵的出现,不仅可以用于分析衍射特性,还能很方便地求解光波在亚波长光栅体内的场分布。修正的适用于亚波长光栅的耦合波分析理论按照如下步骤进行求解:
(1)将光栅区域划分成若干个水平层;
(2)在每一分层中利用快速傅立叶因式分解方法构建耦合波方程,将电磁场空间谐波按勒让德多项式展开;
(3)逐层应用电场和磁场边界连续条件,将各个分层的电场磁通过耦合波方程联系起来;
(4)求解反射和透射的衍射波振幅,将其带到空间谐波方程就可求得光栅体内的光场分布。
由于数值计算只能进行有限项运算,因此在计算时必须对求和项进行截断,这不可避免地会给计算结果带来截断误差。求和子波项数越多,截断误差越小,计算精度越高;但是子波数越多,计算工作量也越大。所以在计算时应在保证计算精度的前提下,减小计算工作量,提高计算速度。在我们的计算中选取勒让德多项式展开的项数为10,空间谐波数为6。数值计算结果表明,这两个参数能够使我们获得足够准确的解,保证了收敛性。
3 亚波长光栅的制备与光谱响应测量
为了在硅片上制备出金光栅结构,我们首先在经过清洁处理的硅片上用电子束蒸发镀上铬层起黏附作用,再旋涂环烯烃聚合物(COP)薄膜。在50 W条件下蒸镀7 min,得到的铬层厚度约为120 nm。接着将环烯烃聚合物(COP)薄膜旋涂在充分清洗的硅片衬底上。COP的透射率为92%,折射率为1.509,热形变温度为123℃。在旋涂过程中要用高于3 000 r/min的转速,保证旋涂出均匀的膜层。使用 SCIVAX、X-200型纳米压印机,在1 000 N压力、150℃条件下压印120 s,结束后将衬底温度冷却到50℃,以10 μm/s的速度将压印模板与衬底直接脱模分离。利用Anelva E-200S溅射系统在制备出的光栅结构上镀Au薄膜120 s,得到的薄膜厚度为200 nm。然后利用反应离子刻蚀机(Samco-10NR型)对纳米复合结构进行刻蚀。用Ar和CF4混合气体在室温下刻蚀上表面的金6 min。用氧反应离子刻蚀(O2RIE)残留的COP层。在气体流速为50 cm3/min、射频功率为100 W、反应时压力为10 Pa的刻蚀参数下,刻蚀速率可稳定在200 nm/min。最后用氯苯、丙酮溶液超声清洗掉光刻胶,就会在硅片上留下需要制备的金光栅结构,周期为1 μm、占空比为0.2。亚波长金属光栅的AFM和SEM照片如图2所示。

图2 亚波长金属光栅的AFM和SEM照片。Fig.2 The AFM and SEM images of the fabricated subwave-length metallic gratings.
在一束TM偏振光以20°入射的情况下,我们使用紫外-可见-近红外光谱仪(V-670:JASCO,Tokyo,Japan)测量了0级反射光谱,结果见图3(b),使用修正矢量衍射理论计算得到的反射谱在图中用虚线画出。在数值计算和理论分析中,对于金属,它们的介电常数的色散和吸收是不能忽略的。金和铬是最典型的Drude金属,其介电常数可用Drude模型来很好地近似。本文取对于金,等离子体频率ωp=8.99 eV,电子的弛豫时间(ωpτ)-1=0.026 78[11]。对于铬,等离子体频率 ωp=4.6 eV,电子的弛豫时间(ωpτ)-1=0.225[11]。

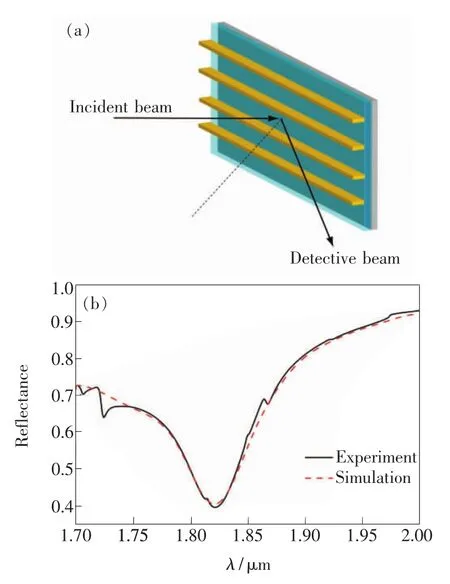
图3 (a)反射光谱测量系统的简单示意图;(b)测量得到的0级反射谱。Fig.3 (a)Schematic diagram of the experimental setup used to measure the grating refiectance spectra.(b)The calculated and measured zero-order reflectance spectra in air.
数值计算所选的参数都与实验制备的样品参数一致。光栅周期为1 μm,金的高度为800 nm,宽度为200 nm,基底材料是Si,在Si上覆盖一层厚度为160 nm 的铬。波长为1.82 μm 和2 μm的TM偏振光以20°入射到光栅表面,计算得到的磁场Hy分布如图4所示。可以看出,我们提出的修正矢量衍射理论可以方便地求解出亚波长光子器件内的电磁波传输特性。同时揭示了以矩形金属为单元的金属光栅表面的共振模式存在两种情况:一种是水平方向的SPR,存在于金属上下表面,是一种水平周期结构引发的共振;另一种存在于金属左右垂直表面的微腔谐振模式。

图4 使用修正矢量衍射分析方法计算得到两种波长对应的磁场分布。Fig.4 The calculated field distribution based on vector diffraction theory.
当入射光束照射到光栅表面时,将产生一系列的衍射光波,当某一级衍射光光波矢在界面方向上的分量与表面等离子体波的波矢相匹配时,二者发生共振,该级次的衍射光波的强度会急剧下降,即产生表面等离子体共振现象。图5为反射谱随光波长和入射角度之间的关系。根据光栅理论,SP共振条件为:

图5 反射谱随光波长和入射角度的变化Fig.5 Reflectance variation with the incident light wavelength and the incident angle

其中λSPP代表表面等离子体共振波长,θ0代表光波入射角度。当待测物质折射率(na)发生改变时,不同衍射级次光波对应的共振波长也会随之变化。研究表明,表面等离子共振条件对于金属表面介质折射率的微小变化非常敏感。因此,当金属表面的介质为一种待测分析物时,则可以通过记录共振角或共振波长的变化来实现对待测分析物折射率的检测,这就是SPR传感器的工作原理。当折射率增加时,正级次衍射光波对应的共振波长增大,而负衍射级次衍射光波对应的共振波长在减小。当待测物质折射率变化量相同时,可以看出,负级次衍射光波对应的共振波长变化量大于正衍射级次光波。

图6 入射光垂直入射到不同深宽比光栅对应的反射光谱Fig.6 The calculated reflectance spectra for gratings with different aspect ratios
当入射光垂直入射到具有不同深宽比的光栅表面时,计算得到的反射谱线如图6所示。对比发现,深宽比为10∶1的光栅的光谱会出现更多的反射谷,这是由于当光栅的深度增加,当入射光波长满足一定关系时,会在光栅槽中形成微腔谐振模式,这是一种类 Fabry-Perot共振模式。根据F-P腔谐振公式:

式中neff为对称金属包裹介质波导模型的有效折射率,λ为入射光波长,m为整数。这种微腔谐振模式对金属光栅的异常透射和光耦合增强均会产生作用,引起了很多研究者的关注[1,12]。
矢量衍射分析方法为研究亚波长尺度下的光传输问题提供了一种技术手段。由于表面等离子激元局限在金属和电介质的表面处,其透射增强作用仅作用于数百纳米的近场,这与传统的透射光栅有所区别。严格耦合波理论的优势在于对于无论何种形状的纳米结构,只要其折射率分布具有周期性,我们都可以快捷的求出衍射效率和光场分布,不像有限差分法那样需要考虑结构的尺寸大小,很难处理大尺寸结构。
4 结 论
使用纳米压印技术结合溅射和反应离子刻蚀工艺制备了一种金属光栅,并使用紫外-可见-近红外光谱仪测量了光栅的反射光谱。根据参考文献[8]提供的方法,在严格耦合波理论的基础上,把光栅区域电磁场的空间谐波通过勒让德多项式展开,通过求解光波在亚波长光栅体内的场分布,得到光栅的反射光谱。同实验测量结果对比发现,修正的矢量衍射分析方法精确地求得了光栅反射光谱的共振波长位置,验证了其分析亚波长光栅的可行性。数值计算结果表明,以矩形金属为单元的金属光栅表面的共振模式存在两种情况:一种是水平方向的SPR,存在于金属上下表面,是一种水平周期结构引发的共振;另一种存在于金属左右垂直表面的微腔谐振模式,这是一种类Fabry-Perot共振模式。本文的研究结果为进一步探索亚波长金属光栅在生物传感、薄膜太阳能电池等领域的应用提供了一定的参考。
[1]Bai W L,Guo B S,Cai L K,et al.Simulation of light coupling enhancement and localization of transmission field via subwavelength metallic gratings[J].Acta Phys.Sinica(物理学报),2009,58(11):8021-8026(in Chinese).
[2]Yang Z L,Fang W J,Yang Y Q.Two-photon-excited fluorescence enhancement caused by surface plasmon enhanced exciting light[J].Chin.J.Lumin.(发光学报),2013,34(2):240-244(in Chinese).
[3]Han J,Fan Y C,Zhang Z R.Propagation of surface plasmon polaritons in a ring resonator with PT-symmetry[J].Chin.J.Lumin.(发光学报),2012,33(8):901-904(in Chinese).
[4]Dinesh A,Sumet H,Prashant T,et al.Fabrication of compliant high aspect ratio silicon microelectrode arrays using micro-wire electrical discharge machining[J].Microsyst.Technol.,2009,15:789-797.
[5]Zhang X W,Ning Y Q,Qin L,et al.Polarization control of 980 nm high-power vertical-cavity surface-emitting lasers by using sub-wavelength metal-gratings[J].Chin.J.Lumin.(发光学报),2012,33(9):1012-1017(in Chinese).
[6]Xiao X X,Chen Y G.Investigation of optical wave coupling between two subwavelengh slits in metallic sheet[J].Chin.J.Lumin.(发光学报),2009,30(5):682-686(in Chinese).
[7]Liu J,Liu J,Wang Y T,et al.Resonant properties of sub-wavelength metallic gratings[J].Chin.Opt.(中国光学),2011,4(4):363-368(in Chinese).
[8]Moharam M G,Gaylord T K.Rigorous coupled-wave analysis of planar-grating diffraction[J].J.Opt.Soc.Am.A,1981,71(7):811-817.
[9]Hooper I R,Sambles J R.Coupled surface plasmon polaritons on thin metal slabs corrugated on both surfaces[J].Phys.Rev.B,2004,70(4):045421-1-14.
[10]Khavasi A,Jahromi A K,Mehrany K.Longitudinal Legendre polynomial expansion of electromagnetic fields for analysis of arbitrary-shaped gratings[J].J.Opt.Soc.Am.A,2008,25(7):1564-1573.
[11]Lynch D W.Hunter W R.Handbook of Optical Constants of Solids[M].London:Academic Press,1985:286-287.
[12]Wang Y W,Liu M L,Liu R J,et al.Fabry-Perot resonance on extraordinary transmission through one-dimensional metallic gratings with sub-wavelength under transverse electric wave excitation[J].Acta Phys.Sinica(物理学报),2011,60(2):024217(in Chinese).

