资本集聚与经济增长的非线性研究——基于系统动态GMM估计和门槛回归的经验分析

王明益

(山东财经大学 国际经贸学院，山东 济南250014)

一、引 言

要素的空间集聚现象是世界经济发展的特征之一，有关要素集聚与区域经济增长关系的研究很多。大多数研究支持了要素的空间集聚对经济增长的促进作用，认为要素的空间集中可以带来技术、知识的外溢、相关产业的前后向关联效应及劳动力市场的外部性等。然而，多数学者忽视了要素(如资本、劳动力、技术等)的空间集聚也会带来一些不利于区域经济增长的因素，如:竞争过于激烈，拥挤效应及资源的过分消耗等。即:要素的空间集聚取决于向心力和离心力的大小对比。短期来看，向心力可能会大于离心力，导致集聚对经济增长产生促进作用，长期来看，离心力可能会大于向心力，导致要素集聚不利于经济增长。因此，要完整的分析要素的空间集中与经济增长的关系，应该考虑时间的动态性。有部分学者对要素的集聚对经济增长的作用产生质疑并进行了相应地经验研究。如:Williamson［1］通过对空间集聚与早期的经济发展关系的研究，认为要素的空间集聚对经济增长的促进作用是逐渐减弱最后可能阻碍经济发展。Bertinelli和Black［2］认为一个地区的经济增长往往从发生要素集聚的地点或城市发起，在集聚初期，集聚产生的收益足以抵消拥挤等造成的成本，但是随着经济发展水平的上升，各种阻碍经济发展的因素造成的成本迅速上升，导致集聚的促进作用逐渐减弱。Longstaff［3］基于墨西哥32个州1994-2000年的面板数据，用每平方公里的人口数来代表集聚水平，实证结果没有发现集聚与经济增长之间的显著相关关系。陈得文、苗建军［4］根据新增长理论和新经济地理学理论构建了空间集聚和经济增长面板数据联立方程，运用GMM三阶段最小二乘法实证检验了1995-2008间中国省域空间集聚和经济增长的内生关系。结果发现，空间集聚对我国区域经济增长存在倒U关系。Weber［5］用1985-2002年的挪威行业数据，以每平方公里的人数表示集聚变量，检验结果也没有发现人口密度对劳动生产率有显著的促进作用。Ciccone［6］利用美国制造业行业数据研究发现集聚和生产率增长之间存在倒U关系。孙浦阳等［7］基于全球85个国家近10年的面板数据，用系统动态GMM估计方法探讨了空间集聚对经济增长的影响。研究结果支持了“威廉姆森”假说，即伴随着国家经济的高速发展，集聚的好处将被削弱。王丽丽、范爱军［8］基于中国28个制造行业的面板数据，认为空间集聚与全要素生产率增长之间存在门槛效应，并得出集聚水平介于0.0155和0.0492之间最有利于促进全要素生产率增长的结论。

现有研究集聚与经济增长的实证文献，虽然实证检验结果几乎全部都验证了集聚与经济增长长期存在非线性关系。但大多存在如下问题或不足:第一，很多学者以产业为研究层面实证检验产业集聚与经济增长的关系，很少有学者从要素集聚(特别是资本集聚)角度分析分析。事实上，产业的集聚是以要素(如:劳动力、土地、资本等)的集聚为基础的，而要素中资本要素(可以包括物质资本、人力资本及技术资本)的集聚对区域经济增长的具有决定性影响［9］。第二，很多相关文献在检验集聚促进经济增长存在门槛效应时，直接建立门槛模型，这样做的后果是若数据搜集不连续或不准确，即便变量间存在线性关系仍可以得到门槛值。

针对现有文献的不足，本文做了如下尝试:第一，检验的是资本集聚而不是产业集聚;第二，实证分析更加严密、符合逻辑。首先建立动态非线性模型，检验资本集聚与经济增长非线性(二次)关系是否存在，在此基础上再检验是否存在门槛效应、确定门槛值及门槛个数，然后修正计量模型分两个样本分别实证分析资本集聚与经济增长的关系。第三，以交易成本为门限变量，并给出了关于交易成本新的计算方法。另外，本文所用数据的时间跨度较长，即从我国全面对外开放(1992)作为起始年份截止到2011年共20年，这相对于诸多学者们一般用10年之内的数据分析两者之间的非线性关系更具实效性和说服力。

二、资本集聚与经济增长非线性关系的经验检验

(一)基本计量模型的构建

期初:

(1)/(2)得:

(4)式两边取自然对数，得:

为分析资本积聚对经济增长的动态影响及捕捉两者可能存在的非线性关系，把被解释变量的滞后项、资本集聚水平的二次项及资本集聚水平与人均国民收入的乘积三项加入到(5)式中，建立如下计量经济模型:

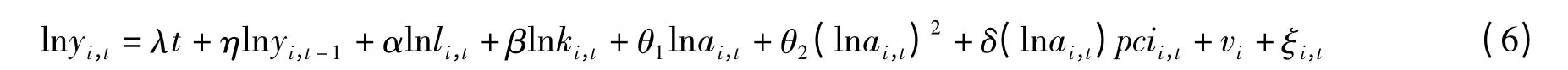
其中，yit表示区域i在t年份相对于基期的经济增长指数，t为时间趋势项，λt表示技术进步对经济增长的贡献，li，t，ki，t，ai，t，pcii，t，vi，ξi，t分别表示i地区报告期的劳动力数量相对于基期的增长指数、资本存量的增长指数、资本积聚的增长指数、人均国民收入指数、不随时间变化的个体效应及随机扰动项。AGGit表示地区i在t期的资本集聚水平。

(二)主要变量说明及数据来源

1.经济增长指数(yi，t):用i地区基期的国内生产总值去除该地区t期的国内生产总值。用来反应i地区报告期相对于基期经济总量的变化。数据来源于全国各省份每年的统计年鉴，西藏自治区因数据不具连续性未列入考查范围。为消除价格波动的影响，i地区报告期的经济总量都用价格指数进行了平减。基期设定为1992年。

2.资本集聚水平(AGGi，t):借鉴克鲁格曼提出的空间区位熵概念，定义地区i在t年份资本积聚水平为:

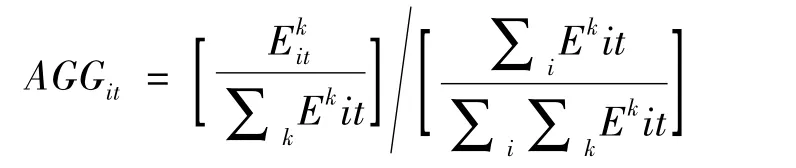
该比值大于1，说明该地区资本集聚水平较高，该比值小于1，说明该地区资本集聚水平较低。其中，资本存量k用的是i地区全社会固定资产投资额与外商直接投资额之和，外商直接投资额根据当年的人民币兑美元的汇率进行计算。

3.劳动力、资本、集聚增长指数(li，t，ki，t，ai，t，pcii，t):各数据分别来自于《中国人口统计年鉴》、《中国劳动统计年鉴》、中国数据在线数据库(China Data Online)、《中国制造业统计年鉴》、《中国统计年鉴》、《新中国55年统计资料汇编》并经过作者简单计算整理所得。其中，各地区资本存量指数、人均国民收入指数都经过价格指数进行了平减。面板数据时间跨度为1992-2011年，共20年①因为研究资本集聚对经济增长的跨期影响，故时间跨度较长。。

(三)实证检验及结果分析

因式(6)是一动态模型，考虑到系统内生性问题，以该式为计量模型，使用系统动态GMM方法估计。系统GMM估计是在差分GMM估计基础上引入了水平方程，并以滞后的差分变量作为水平方程的工具变量，只要工具变量的滞后期数相对较长，最终会使估计结果比差分GMM估计更具有效性和一致性。根据Arellano和Bond［10］提出的动态GMM估计的工具变量选择方法和动态模型(6)一阶差分数据，用内生变量(lnyi，t-1，lnai，t)的水平值及滞后三期值作为工具变量，这样可以有效地消除面板数据中不可观测的个体效应(vi)的影响。此外，使用系统的Sargan检验及相应的p值来衡量系统工具变量总体的有效性。表1是各变量名称、英文符号及描述性统计。

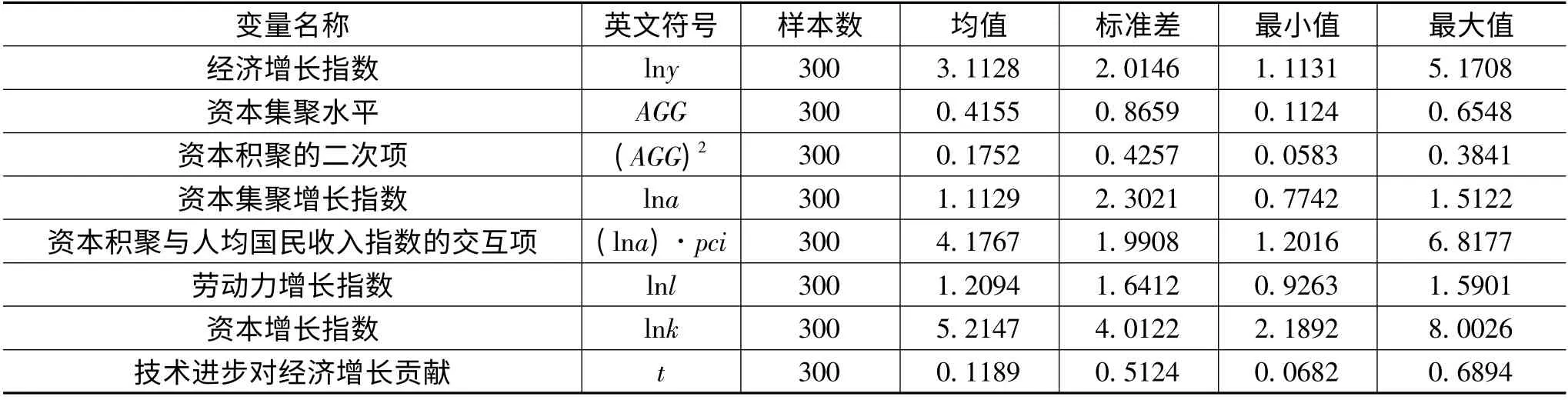
表1 各主要变量的描述性统计特征

使用Stata10.0软件对资本集聚与经济增长间的动态关系进行实证分析，结果见表2。表2对4个模型进行实证检验。模型一没有纳入资本集聚的平方项及资本积聚与人均国民收入指数的交互项这两个变量，结果发现，资本集聚对经济增长的影响是不显著的，原因是在所选时间段的不同时期资本集聚对经济增长影响不同(前期资本集聚对经济增长影响为正，而后期影响为负)。模型二是在模型一的基础上加入了资本集聚水平的平方项，用来捕捉资本集聚与经济增长间可能存在的二次关系。结果发现，在10%的显著性水平上发现了两者之间存在二次关系(倒U型)。模型三是在模型二的基础上又加入了资本集聚水平与人均国民收入①用每省各年份的人均国民收入指数来衡量每个地区经济增长的动态性。其数据根据各省《统计年鉴》并用价格指数进行平减而得。的交互项，目的是进一步检验资本集聚与经济增长间的长期关系。数值是-0.012，并且通过1%的显著性检验。可以理解为资本集聚对经济增长贡献率是逐年下降的，下降幅度为1.2%。模型三的检验结果证明，资本集聚对经济增长的影响是动态变化的，贡献率是逐年下降的，这也间接证明了模型二的实证结论。模型四用的是增长收敛型截面数据回归方法，没有考虑资本集聚对经济增长在时间维度上的变化。其实证结果诸多都不能通过显著性检验。通过截面回归和门槛回归两种估计方法的对比，验证了本文所使用的系统动态GMM估计方法的正确性和合理性。

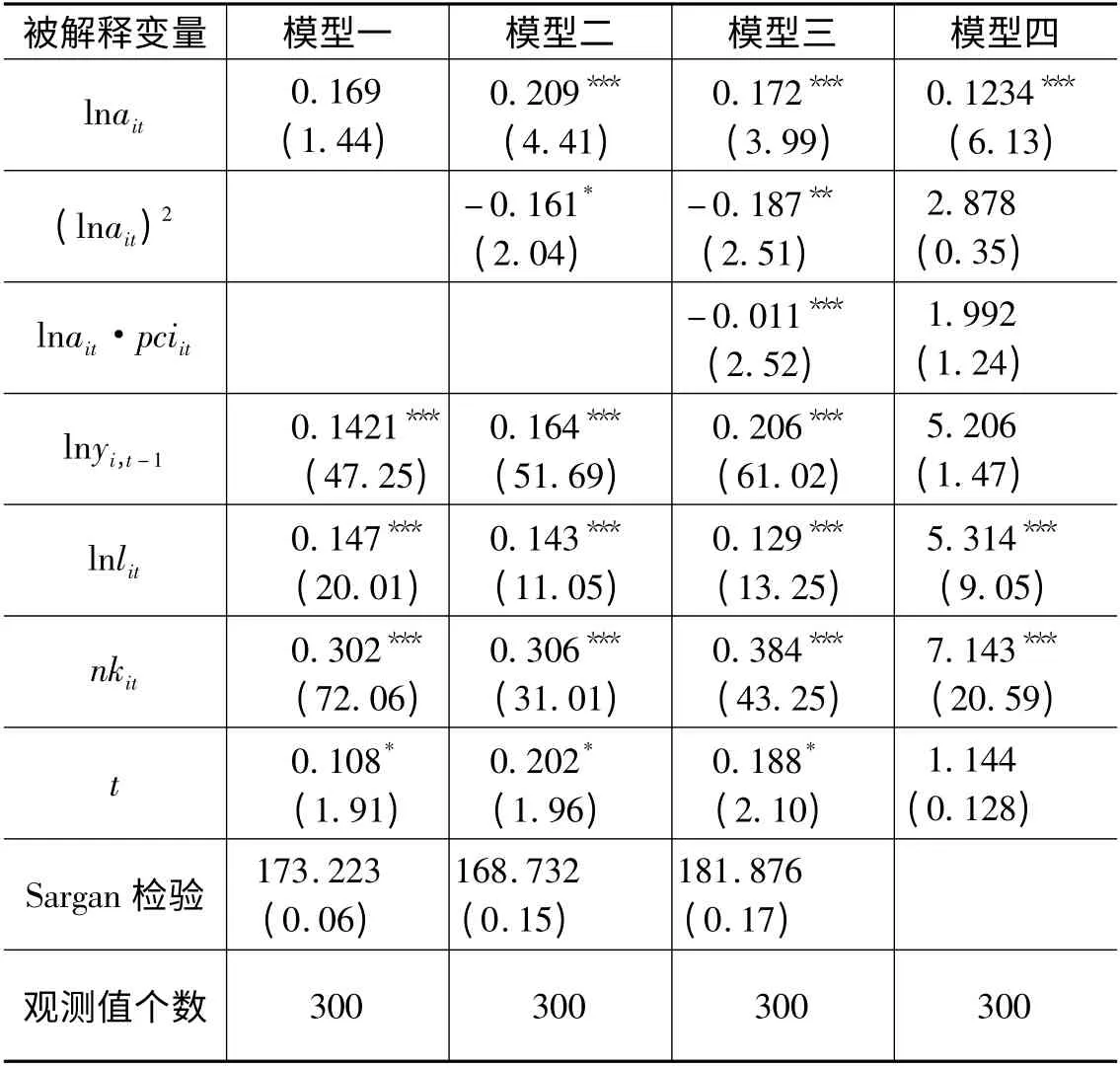
表2 资本集聚与经济增长动态关系检验结果(系统GMM估计)

三、资本集聚与经济增长的门限模型构建及分析

(一)门槛回归简介

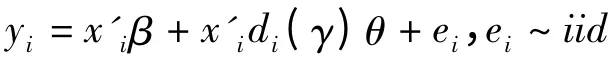
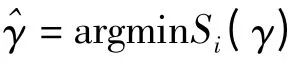
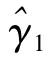
(二)统计检验及门槛模型构建

1.统计检验结果

本实证检验所运用的软件是MATLAB7.0。

由图1可知，在交易成本lntc=10.99%时，Si(γ)残差平方和取得最小值20.98。在交易成本的其他水平上，Si(γ)残差平方和都在60-90范围内取值。图1表明只存在一个门槛值。

由表3可知，检验结果显著拒绝了不存在门槛值的假设，接受了存在一个门槛值的假设。这与图1一致。

图1 单门槛模型回归残差平方图

表3 门槛值存在性、门槛个数及显著性检验结果

表4给出了门槛值的置信区间和Bootstrap P值。由表4可知，在95%的水平上门槛值的置信区间是:［0.0876，0.1195］。Bootstrap P值很小，可以在1%显著水平下拒绝不存在门槛效应的原假设。

表4 门槛估计值及置信区间

2.计量模型的修正

根据对相关数据的统计性检验，可知上述所构建模型只含有一个门限值，根据第二部分的理论推导，把交易成本①交易成本指货物从装运地到目的地产生的费用支出，即到岸与离岸价格之差，计算公式为:。指数(lntc)作为门限变量，修正模型(6)后得到:

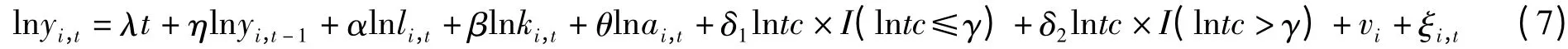
其中I(·)为指示函数，γ为交易成本门限值。表5为门槛回归与普通面板回归结果。

表5 普通面板回归和门槛回归结果

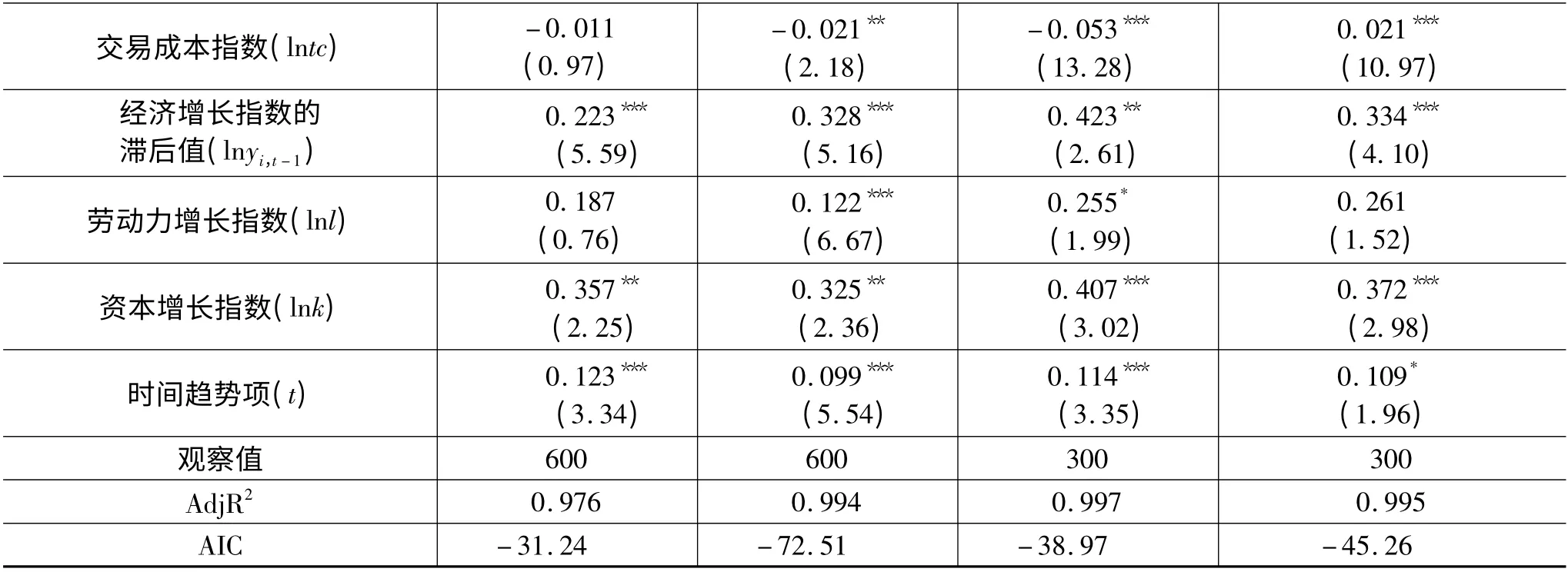
续表5

表5中，模型1是普通面板线性回归结果(本模型中没有纳入资本集聚水平的二次项)，结果没有发现资本集聚对经济增长显著的推动作用(原因同表2对模型一的分析)，也没有发现交易成本的“门槛”作用。模型2是对整个样本进行的门槛回归，结果发现，设定门槛变量后，资本集聚能够在5%的水平上显著地推动经济增长，贡献率为15.3%，也在1%的显著性水平上捕捉到了资本集聚与经济增长间的非线性关系;交易成本在5%的水平上起到了显著性作用。模型3是在交易成本低于门槛值(lntc＜0.1099)条件下的分样本门槛回归结果，我们发现在交易成本(本文指运输及保险费用)较低时，资本集聚动力不足，其对经济增长贡献率仅为13.9%，交易成本对经济增长的贡献度为-2.1%。模型4是在交易成本较高(lntc＞0.1099)时的分样本门槛回归结果。结果发现在交易成本较高时，资本集聚动力得到加强，其对经济增长贡献率达到21.2%，并且通过了1%水平上的显著性检验。相对较高的交易成本构成了资本集聚的动力，从而也间接地促进了经济增长，其对经济增长的贡献率为2.1%。

四、结论及政策建议

本文基于改进的C-D生产函数构建动态非线性计量模型，利用中国1992-2011年共20年、30个省的面板数据，首先验证了资本集聚与经济增长间的非线性关系的存在性。然后对计量模型进行修正建立了门槛回归模型，验证资本集聚与经济增长间是否存在门槛效应。结果表明:资本集聚与经济增长间存在单一门槛值，并基于该门槛值对样本数据进行了分样本门槛回归，门槛回归结果表明，资本集聚与交易成本存在此消彼长的关系，当交易成本较高时，资本集聚动力较足(此时资本收益率较高)，随着交易成本的逐渐降低，资本集聚的动力逐渐减弱(此时其贡献率逐渐下降)，当资本集聚水平跨过交易成本门槛(也即资本集聚水平超过最优状态)后，对经济增长的贡献会明显下降甚至有可能为负值。据此提出以下政策建议:

第一，随着沿海经济发达地区基础设施建设日趋完善，交通网络日益发达，交易成本会逐渐降低，资本自身集聚动力会减弱，资本集聚的负面效应会逐渐凸现出来，但当地政府却容易忽视这一规律，仍通过某些优惠政策加强资本的集聚，其结果很容易造成资本集聚超过最优水平，导致行业竞争过于激烈，资本贡献率会大幅下降。在此情况下，有关管理部门应该加强对部分资本集聚过度的行业进行资本流向管理及政策引导，让过剩资本流向周边及西部资本相对短缺的地区。

第二，中西部地区，交通条件相对落后，交易成本较高，资本集聚动力较足，此时应该进一步制定相关优惠政策措施、加大教育投入力度，提高当地人力资本水平，创造良好的制度、人文及生态环境，增强对外部资本的吸引力加强资本集聚的动力，充分利用资本集聚带来的积极效应来加快地区经济增长。

第三，为了更好地发挥资本集聚的积极效应，有关部门应加强对各种资本本身质量的考核与监管。我国应该进一步完善各种资本的引进、引导或生成机制。对于物质资本，可以通过引入优质FDI及国内金融部门的创造获取，对于人力资本(或技术资本)，应加大投资力度，树立正确的生成、培养机制，以便让其对经济增长发挥更大的作用。

［1］WILLIAMSON G.Migration and Urbanization［J］.Handbook of Development Economics，1983，1(7):425-465.

［2］BERTINELLI B，BLACK A.Theory of Urban Economical Growth［J］.Journal of Political Economy，1987(17):252-284.

［3］LONGSTAFF G B.Rural Depopulation and Urbanization［J］.Journal of the Royal Statistical Society，1993，56(9):77-89.

［4］陈德文，苗建军.人力资本集聚、空间溢出与区域经济增长［J］.产业经济研究，2012(4):54-62.

［5］WEBER A F.The Significance of Recent City Growth:The Era of Small Industrial Centres［J］.Annals of the American Academy of Political and Social Science，1904，23(5):148-159.

［6］CICCONE A M，HALL R.Productivity and the Density of Economic Activity［J］.American Economic Review，1992，87(11):54-70.

［7］孙浦阳，武力超，张伯伟.空间集聚是否总能促进经济增长:不同假定条件下的思考［J］.世界经济，2011(10):3-19.

［8］王丽丽，范爱军.空间集聚与全要素生产率增长［J］，财贸经济，2009(12):105-110.

［9］BALDWIN R，MARTIN P.Agglomeration and Regional Growth［J］.Handbook of Regional and Urban Economics，1985(2):128-144.

［10］ARELLANO I，BOND P.Some Tests of Specification for Panel Data:Monte Carlo Evidence and Application to Employment Equations［J］.Review of Economic Studies，1991(4):277-297.

［11］HANSEN E.BRUCE.Estimation and Inference in Models of Cointegration:A Simulation Study［J］.Advances in Econometrics，1996(6):225-247.