准谐振控制器在抑制永磁同步电动机共模电压上的应用

黄守道 张文娟 高 剑 肖 磊

（湖南大学电气与信息工程学院 长沙 410028）

1 引言

随着电力电子技术的发展，尤其是先进的全控型功率半导体器件，如绝缘栅双极晶体管（IGBT）、集成门极换向晶体管（IGCT）、智能功率模块（IPM）等的出现，微电子技术及控制技术的发展，促进了变流技术的发展，出现了以脉宽调制（PWM）为基础的各类变流装置。尤其是电压源型PWM变流器，因其具有交流电流低谐波，单位功率因数，开关频率高，通态压降低等特点，在电动机的控制中被广泛应用。采用 IGBT做成的通用型变频器，其开关频率可高达20kHz，最低输出频率也可达0.5kHz[1]。用它控制电动机运行，噪声更小，运行也更为平稳。但随着载波频率不断升高，由变频器产生的高频共模电压对电动机的负面效应也更为显著。由于其高频特性和电压的快速上升，对电动机驱动系统产生了非常大的危害。如何消除这些影响是当前国内外研究的热点。文献[2,3]采用隔离变压器法，该方法将共模电压从电机侧转移到了隔离变压器次级，这需要提高变压器的耐压能力。文献[4,5]运用新的PWM 开关技术来抑制共模电压。文献[6]提出了逆变器输出有源滤波器结构，通过设计特殊的有源滤波器将共模电压消除。本文从共模电压产生的机理出发，推导出共模电压是以载波频率为中心，边频带宽±kω（ω调制波频率，k=1，2，3…）分布其两侧，幅值对称衰减的谐波，其最高幅值在载波频率处。针对这一特点，选用指定频率下的准谐振控制器，使其谐振频率为载波频率，通过调整其截止频率，来实现对共模电压的零稳态误差控制。

2 共模电压产生机理

以最常用的两电平SPWM为例，其变频器的拓扑如图1所示。

图1 两电平变频器拓扑图Fig.1 Topology of two-level inverter

设三相绕组中的共模电压为 VCM，电机绕组中的等效阻抗为 Z，三相绕组感应电动势为 eA、eB、eC，三相电流为IA、IB、IC。

式中，UA、UB、UC为逆变器A、B、C三相电压。在三相绕组为对称负载时，有

把式（2）代入式（1），整理得

由文献[7]可知变频器输出三相电压傅里叶展开式为

式中 Vdc——直流母线电压；

a——调制深度，通常设定为1；

ω1——调制波角频率；

ωs——载波角频率。

将式（4）代入式（3）中，再利用贝塞尔函数可以得到共模电压的傅里叶表达式为

也就是说，共模电压是以载波 nωs为中心，边频 kω1分布其两侧，幅值两侧对称衰减的谐波，并且在载波频率处的谐波幅值最高，针对共模电压这一特点，引入准谐振控制器，使其谐振频率为载波频率，通过调整其截止频率来增加它的带宽，来实现对共模电压高幅值处的跟踪补偿控制，以达到抑制输出共模电压的目的。

3 传统PI控制

对于表贴式永磁同步电机（PMSM），其数学模型为

式中 p——电机的极对数；

ψf—— 永磁体磁链；

id，iq—— 定子电流直轴、交轴分量；

ud，uq—— 定子电压直轴、交轴分量；

Ld，Lq—— 定子直、交轴电感，且Ld=Lq；

ωe—— 电角速度。

基于磁场定向的永磁同步电动机控制框图如图2所示。

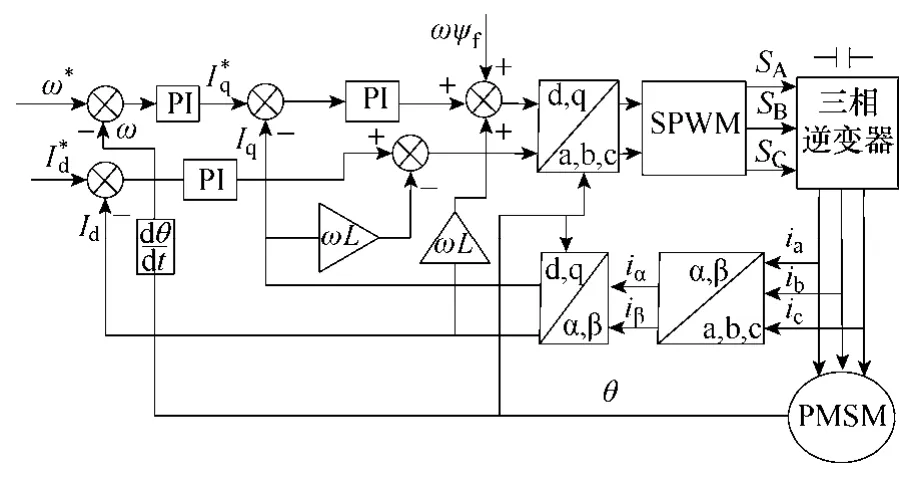
图2 PMSM传统控制框图Fig.2 The conventional control diagrom of PMSM

当电流调节用传统的PI控制时有

式中 kpl, kil——PI中的比例系数和积分系数；——电流、电压指令。

将式（8）代入式（7）有

从式（9）可以看出，当基于前馈的PI控制时，可以使id、iq实现完全解耦。但PI控制器只能在同步旋转坐标系下，对直流电信号进行有效的稳态无差控制，对交流谐波信号难以达到理想的控制效果[8]。如果在 PI控制的基础上并联谐振控制（resonant controller）环节，构成PI-RES控制器，利用谐振控制器可使频率与其谐振频率相同的正弦信号实现零稳态误差控制的特点。采用谐振频率为载波频的谐振控制器，选定适合的截止频率，对共模电压高幅值段进行重点补偿，来达到对输出共模电压的抑制效果。

4 基于准谐振控制器的控制策略

4.1 PI-RES控制器

理想谐振控制器的传递函数为

式中 ki——积分系数；

ω0——谐振频率。

从图4可以看出，谐振控制器在谐振频率ω0处增益无穷大，而对其他频率的信号基本不产生影响，这样可以使与谐振频率具有相同频率的正弦信号实现零稳态误差控制[9]。

但是在实际应用中，理想的谐振控制器无论是在模拟还是数字系统中都无法实现。当实际频率与设计频率略有偏差时，谐振控制器的增益将大幅下降，为了改进这个问题，现在基本采用准谐振控制器，其传递函数为

式中，ωc是截止频率。

正是通过设定合适的ωc而减少准谐振控制器对信号频率变化的敏感度，提高了系统的控制性能。

图3是改进后的控制系统模型，由于电流环的对称性，下面仅给出d轴控制器模型。

图3 d轴PI-RES控制器模型Fig.3 Block diagram of the proposed current control sheme of d-xias

4.2 零稳态误差控制的实现

从准谐振控制器的传递函数可以看出，它与数字信号处理中的带通滤波器是一致的。只对谐振频率处的信号起作用，而对其他频率信号有很强的衰减作用。在本文也就是只对误差量中频率为载波频率 eiwc那部分谐波起控制作用。由图3可以写出闭环控制的传递函数为

当G(s) 为理想谐振控制器时，在ω0处的增益无穷大。在式（13）中第一项等于Iref；第二项为0。当G(s) 为准谐振控制器时，虽然其谐振频率处增益不能像理想谐振控制器那样无限大，但仍然可以使第一部分约等于Iref；第二部分约为0。

其实现可以使用双线性变换，变换公式为

式中 T——采样频率；

a=ω0。

将其代入式（11）可得到离散化传递函数

整理后得到控制器的差分方程为

由上式即实现了对误差信号的稳态控制，并且可以看出控制比较简单，容易实现。

4.3 PI-RES控制器的设计

PI-RES控制器的设计主要就是PI-RES的参数设计。其中 PI的参数设计已经有大量的文献介绍过，本文主要是针对 RES参数进行优化设计。由RES的传递函数可以看出，控制器的增益与kr成正比，随着ωc的增加，控制器的带宽增大。对于理想状态是kr、ωc越大越好，当设定RES的谐振频率为载波频率后，kr与ωc存在最优配置。当kr过大会影响系统的稳定性和收敛性；当ωc过小时，对谐振波的抵制效果大大减弱，甚至会起反作用；而过大时会引起控制器选频特性变差，影响控制性能[10]。本文根据经典控制理论，选定最佳的 kr、ωc。从图 4可以看出当 kr=2000时，令ωc=10rad/s时对谐波的抑制效果达到最佳。

图4 参数变化下的RES控制器波特图Fig.4 Bode diagram of the resonant controller in variable parameters

5 仿真与实验

5.1 仿真研究

运用Matlab/Simulink软件，对比分析采用PIRES控制器前后，输出共模电压的情况。其中，仿真和实验用的电机参数为：额定功率为2000W，额定电压为380V，额定转速为1500r/min，定子相电阻为 0.86Ω，定子电感为 11.3mH，永磁体磁链为0.205Wb，极对数为 2，载波频率为 3kHz。仿真模型中 PMSM采用转子磁链定向 Id=0控制策略，额定转速给定1500r/min模式。

图5为采用传统PI控制器与采用PI-RES控制器下共模电压、三相电流对比仿真波形。其中图5a中，共模电压幅值为275V，波动大，图5b中由于准谐振控制器对载波频处的高幅值共模电压的抑制作用，从波形上看，共模电压幅值为125V，波动减小。再比较图5c、5d可见，由于共模电压高幅值部分得到了有效抑制，图 5d中三相电流谐波较图 5c有很好的改观，电流的正弦性更好。

图5 仿真波形对比Fig.5 Comparation of the simulation waveforms

5.2 实验研究

为了更好的验证仿真研究的正确性，建立了实验系统对 PI-RES控制器对共模电压的抑制进行实验验证（见图6）。系统采用Ti公司的TMS320F2812为主控芯片，PWM载波周期为3kHz，电机参数与仿真模型参数保持一致。实验结果采用 QualityStar功率分析仪进行采集。

图6 实验用电机与驱动系统Fig.6 The PMSM and drive system of the lab

为了更好地观察对比实验结果，图7均采样一个周期。由图 7a、7b可以看出，PI-RES控制器对共模电压有很显著的抑制作用，尤其是对高幅值部分的补偿效果明显。在采用了 PI-RES控制器后，共模电压的幅值相当于在PI控制器中的39%。但仍然不能完全抑制，其主要原因是：只是对载波频率处的高幅值谐波进行了重点补偿，而其他频率处的谐波含量仍然较大。

图7 实验波形对比Fig.7 Comparation of the experiment waveforms

图7c、7d为采用PI与PI-RES控制器的三相电流波形。当采用了 PI-RES控制器对载波频率处的谐波进行补偿后，电流的畸变率有所降低，谐波含量减小。可以看出在对共模电压的高幅值部分进行有效的抑制后，能够得到更平稳的系统输出，有利于提高整个系统的性能。从实验结果可以看出实验与仿真结果一致，验证了 PI-RES控制器在抑制共模电压上的有效性。

6 结论

本文从共模电压产生机理出发，在传统PI控制器中并上了RES控制器组合成PI-RES控制器，从其传递函数推导出了其对载波频率下高幅值共模电压零稳态误差控制的实现过程。设计最佳参数并用于仿真模型，以仿真波形验证了本文提出的控制策略的有效性。最后搭建相应的实验系统，实验结果表明在传统的PI控制器上再并联RES控制器构成的 PI-RES控制器可以抑制电动机的共模电压，对共模电压的抑制研究有一定的实际意义。

[1]王久和.电压型PWM整流器的非线性控制[M].北京: 机械工业出版社,2008.

[2]Rizzo S, Xiao Y, Zargari N.Medium voltage drive review[C].PCIM Power Electronics Conf.,2000:182-195.

[3]Hammond P W.A new approach to enhanced power quality for medium voltage drives[J].IEEE Trans.IA,1997, 33(1): 202-208.

[4]Julian A, et al.Elimination of common-mode voltage in three-phase sinusoidal power converters[J].IEEE Trans.on Power Electronics, 1999, 14(5): 982-989.

[5]Kim Lee Hum, Park Hyun Seok, Jeong Gil.A new switching technique for conducted EMI reduction of PWM-inverter AC motor drive system[C].ICMIT,2003: 150-156.

[6]姜艳姝, 刘宇, 徐殿国, 等.PWM 变频器输出共模电压及其抑制技术的研究[J].中国电机工程学报2005,25(9): 47-5 3.Jiang Yanshu, Liu Yu, Xu Dianguo, et al.Reserch on commom-mode voltage generated by a PWM inverter and its cancellation technology[J].Proceedings of the CSEE,2005,25(9): 47-5 3.

[7]Grahame D Holmes, Thromas A Lipo.Pulse width modulation for power converters;principles and practice[M].New York: Wiley Publishing, Inc.,200 3.

[8]肖磊, 黄守道, 黄科元, 等.直驱永磁同步风力发电机机侧变流器谐波抑制[J].中国电机工程学报,2011, 31(6): 31-37.Xiao Lei, Huang Shoudao, Huang Keyuan, et al.Harmonic suppression for the motor-side converter of the directly-driven wind turbine with PM synchronous generator[J].Proceedings of the CSEE,2011, 31(6):31-37.

[9]杨秋霞, 梁雄国, 郭小强, 等.准谐振控制器在有源电力滤波器中的应用[J], 电工技术学报,2009,24(7): 171-176.Yang Qiuxia, Liang Xiongguo, Guo Xiaoqiang, et al.Application of quasi resonant controller for active power filter[J]. Transactions of China Electrotechnical Society,2009,24(7): 171-176.

[10]黄沁, 李耀华.一种新颖的含有谐振控制器的CVCF逆变器多环反馈控制方法[J].电工电能新技术,2004,24(2): 37-40.Huang Qin, Li Yaohua.A novel multi-loop control method with resonant controller for CVCF inverter[J].Advanced of Technology of Electrical Engineering and Energy,2004,24(2): 37-40.