分数槽集中绕组永磁电机在模块化级联电机系统上的应用

韩守亮 崔淑梅 王铁成 陈清泉 张鑫鑫

（哈尔滨工业大学电气工程及自动化学院 哈尔滨 150001）

1 引言

模块化级联电机（Modular Cascade Machines，MCM）系统，像电池一样，把一个电机单元作为一个模块，多个电机模块级联式工作（见图1）。可以根据需要选择电机组合的方式：若模块电机相同，功率需求不同只需要改变电机数目即可；若模块电机不同，而外部连接结构相同，可以根据系统所需的外特性来决定电机的个数和特性，从而得到更好的外特性。MCM 系统可有效地增加系统高效区范围，提高容错能力，降低研发成本[1]。

图1 MCM系统模型示意图Fig.1 View of MCM system

但是，对于MCM系统来说，由于多模块电机级联工作方式，不能简单地采用传统电机作为电机单元。首先，要使得MCM的功率密度和转矩密度与传统电机相当，就需要减小单个模块电机的体积和重量；其次，多个电机轴刚性互联，并且不易发生扰动，就需要使单模块电机的轴向长度尽可能短，电机以扁平状结构为宜。由于分数槽集中绕组永磁电机，能有效地缩小电机尺寸并增加效率，提高功率密度、增加弱磁扩速能力，节约成本[2,3]，适合作为MCM系统的单模块电机。

分数槽集中绕组永磁电机通过等效分布的作用，削弱了电动势的谐波成分，以达到改善电动势波形和提高绕组利用率的效果；但是定子电流会产生分数次谐波，谐波含量较多，在转子内感应的涡流损耗较强，会引起很高的温升，从而引起永磁体局部退磁。电机的分数槽能削弱齿谐波，有效地减小永磁电机的定位转矩，但是某些槽配合具有不平衡磁拉力以及振动噪声变大等负面影响[4]。

本文通过分析分数槽集中绕组永磁电机的槽极数的配合规律，初步设计了满足MCM系统性能指标的两台不同性能的单模块电机，通过对其磁动势的谐波分析和涡流损耗计算，优化了所设计的样机，并仿真了样机的效率Map图，最终对MCM进行了实验研究。

2 槽极数配合选择

永磁电机的槽极数如何选择有较多的标准，但通常将高转矩密度、高效率作为基本的选择标准。而分数槽电机的绕组设计需要遵循一定的约束条件，并不能随意地选取[5]。

只有满足下面公式的槽极数配合才是可取的

式中 Z——定子槽数；

m——相数；

GCD——最大公约数；

p——极对数；

k——整数。

若要做成集中绕组电机，即电机绕组节距为1，则电机的槽极数关系需满足[6]

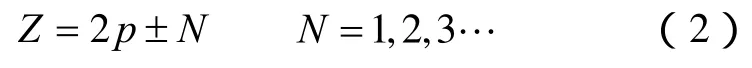
在式（1）、式（2）的约束下，尽可能选取绕组分布系数较大的组合，因为它的EMF基波较大；极数要根据电机的转速要求和效率指标来选择，因为极数越大，频率就越大，此类型电机谐波含量较多，会在转子内感应较强的涡流损耗，降低效率。

因此，在本文的MCM系统中，按照性能指标的要求，分别选择极槽数为24/20、12/10两种组合来设计单模块样机，它们峰值功率相同，转速范围不同，部分参数结果见表 1。样机如图2所示，样机的端盖和轴经过特殊设计，以方便它们互联，并且在两端均可安装位置传感器。

由表1知，对相同体积和重量的电机，功率密度和转矩密度是相反的两个指标，经常运行在低速区时，可以将转矩密度设计得较大，获得较大的起动力矩；而经常运行在高速区时，可以将功率密度设计得较大，获得较高的高速功率。MCM 系统将两者相结合，在全转速范围内获得较好的运行性能。

图2 实验用样机Fig.2 The prototypes for test

3 磁动势谐波分析与涡流损耗计算

普通永磁电机转子内的磁通密度基本不变，涡流损耗可以忽略，但是，分数槽绕组电机定子绕组会产生较大的谐波磁动势[7,8]。从磁动势角度看，有效转矩是空间谐波磁动势和永磁转子磁场相互作用产生的，其他相对于转子的正向或反向旋转谐波磁动势作用下将会在转子（包括永磁体）产生涡流并造成损耗，使转子永磁体温度上升，甚至引起退磁。

3.1 磁动势分析

定子三相绕组之间相差2π/3空间电角度，绕组星形联结。以定子A相绕组轴线处作为空间坐标原点，取A相绕组电流由负变正时刻为时间起点，当对称的三相绕组通入时间上彼此相差 2π/3电角度的对称三相正弦电流时，在某一瞬间 t，距离 A相绕组轴线θ 处，A、B、C三相绕组各自产生的谐波脉振磁动势为

式中 Fφv——相磁动势谐波幅值；

υ——定子磁动势空间谐波次数。

则三相绕组谐波合成磁动势为

通过对式（4）的三相绕组谐波合成磁动势分析，可以得出以下结论：

（1）υ=1，三相绕组谐波合成磁动势为正向旋转，转速为ω，幅值是相绕组该谐波磁动势振幅的3/2。

（2）υ=3k（k=1,2,3,…）的三相合成磁动势为0，即谐波次数为3的整数倍的合成磁动势为0，与传统三相交流电机绕组一样。

（3）υ=3k±1（k=1,2,3,…）的三相合成磁动势为 0，因为定子槽数为偶数，谐波次数为偶数的合成磁动势为0。

（4）υ=6k-1（k=1,2,3,…）的三相合成磁动势为反向旋转，转速为ω/υ，若与主波转速不一致，将会产生转矩脉动。

（5）υ=6k+1（k=1,2,3,…）的三相合成磁动势为正向旋转，转速为ω/υ，若与主波转速不一致，将会产生转矩脉动。

本文中，两台样机分别是24槽20极、12槽10极，根据定子合成磁动势的推导可知，两台样机基波电流产生的磁动势谐波分别为1次（正向）、5次（反向）、7次（正向）、11次（反向）、13次（正向）、17次（反向）、19次（正向），…。由于每极每相槽数为 2/5，主波磁场是 5次，如果将 5次主波看作是基波，则谐波次数为1/5、1、7/5，…。

采用二维有限元仿真软件分别对两台样机的电枢磁动势进行仿真，采用电流源激励，施加额定电流，忽略漏磁的影响，磁动势谐波分析如图3所示。

由图3可以看出，幅值较高的磁动势谐波次数有1、5、7、17、19、29、31, …，包含1/5次次谐波，与理论分析一致。

图3 三相绕组电枢磁动势谐波分析Fig.3 Harmonic analysis of 3-phase winding armature magnetomotive force

同样，对电枢电流为0时的转子磁动势进行谐波分析，结果如图4所示。转子主要产生5次主波（基波）和15次（3次）谐波。

图4 转子磁动势谐波分析Fig.4 Harmonic analysis of rotor magneto-motive force

3.2 涡流损耗计算

从上文分析可知，对于分数槽电机，与转子转速不同的低次空间谐波分量是产生较大转子涡流损耗的主要因素。具体地说，永磁电机的转子涡流损耗主要由以下几个因素共同引起：①定子开槽引起的气隙磁导率变化；②定子绕组分布的空间谐波；③定子电流中的时间谐波[9,10]。

本文采用二维有限元法分别计算两台样机的转子铁心涡流损耗、永磁体涡流损耗和定子铁心涡流损耗。铁心涡流损耗可以认为是径向磁通密度 Br和圆周方向磁通密度Bθ共同作用的结果，按式（5）进行时步有限元计算[11]

式中 D——铁心密度；

N——每个周期下的时间步长；

Δt——时间间隔；

Ke——Epstein测试得到的经验系数。

永磁体的涡流损耗采用式（6）进行计算[12]

式中 Jn——第n次谐波涡流的幅值；

σ ——永磁体电导率；

V——永磁体体积。

基于分析的简便性，文中分别对空载和额定负载情况下的涡流损耗进行计算，两台电机的参数分别为：电机I频率为166.7Hz，电流1 2.8A；电机II频率为208.3Hz，电流1 2.8A；负载情况下，忽略定子电流的时间谐波所造成的损耗，即只进行定子基波电流所产生的涡流损耗计算，结果见表2。

表2 样机涡流损耗计算结果Tab.2 Calculated results of eddy current loss in prototypes（单位：W）

从表2中可以看出，负载时转子涡流损耗特别是永磁体涡流损耗比空载时大大增加。这是因为，空载时，转子涡流损耗主要是由定子槽开口所引起的气隙磁导变化所产生的，即当永磁体任意点从面对齿顶转到面对槽开口时，面临的气隙磁导是变化的，使得永磁体内磁场发生变化，产生涡流损耗。负载时，除了空载损耗外，由于定子绕组非正弦分布而产生的空间谐波，会使定子电流基波和时间谐波（本文未考虑）在转子中产生涡流损耗，而根据图3的分析，分数槽集中绕组的磁动势空间谐波较大，使得转子涡流损耗快速增加。

由于转子涡流损耗在负载时增加较大，因此在采用分数槽绕组时，必须采取适当的方法减小涡流损耗，由上述分析可知，主要从气隙磁导、定子绕组空间谐波、定子电流时间谐波三个方面去改善，相关文献已经进行了大量的研究[13-15]，对于本文中的MCM系统用分数槽永磁电机，主要从槽口宽度和永磁体分块方面研究转子涡流损耗的变化情况。

图 5是槽极数为24/20的电机 I采用不同槽口宽度时，空载和负载情况下转子涡流损耗的变化曲线。从图5可以看出，随着槽口宽度的增加，转子涡流损耗随之增加，这是由于槽开口加大使气隙磁导变化剧烈，导致涡流损耗加大。但槽开口的影响主要表现在转子空载涡流损耗中，特别是当槽开口大于3mm时，转子空载涡流快速增加，而对负载时涡流损耗影响稍小，在设计时需要综合考虑电机槽满率、工艺性再选择合适的槽口尺寸。

图5 转子涡流损耗随槽口宽度变化曲线Fig.5 Curves of rotor eddy current loss with width variation of notch

由于在中低频磁场下，谐波磁场在永磁体中的透入深度远大于永磁体的厚度和周向宽度[16]，永磁体分块能有效减小永磁体涡流损耗。假设忽略永磁体中涡流磁场对谐波磁场的屏蔽作用，图6是槽极数为 24/20的电机 I每极采用不同永磁体块数时，空载和负载情况下转子涡流损耗的变化曲线。从图6中可以看出，永磁体分块能明显地减小永磁体空载和负载时涡流损耗，对于本文中电机 I每极采用3块永磁体，可以有效抑制永磁体中的涡流损耗。

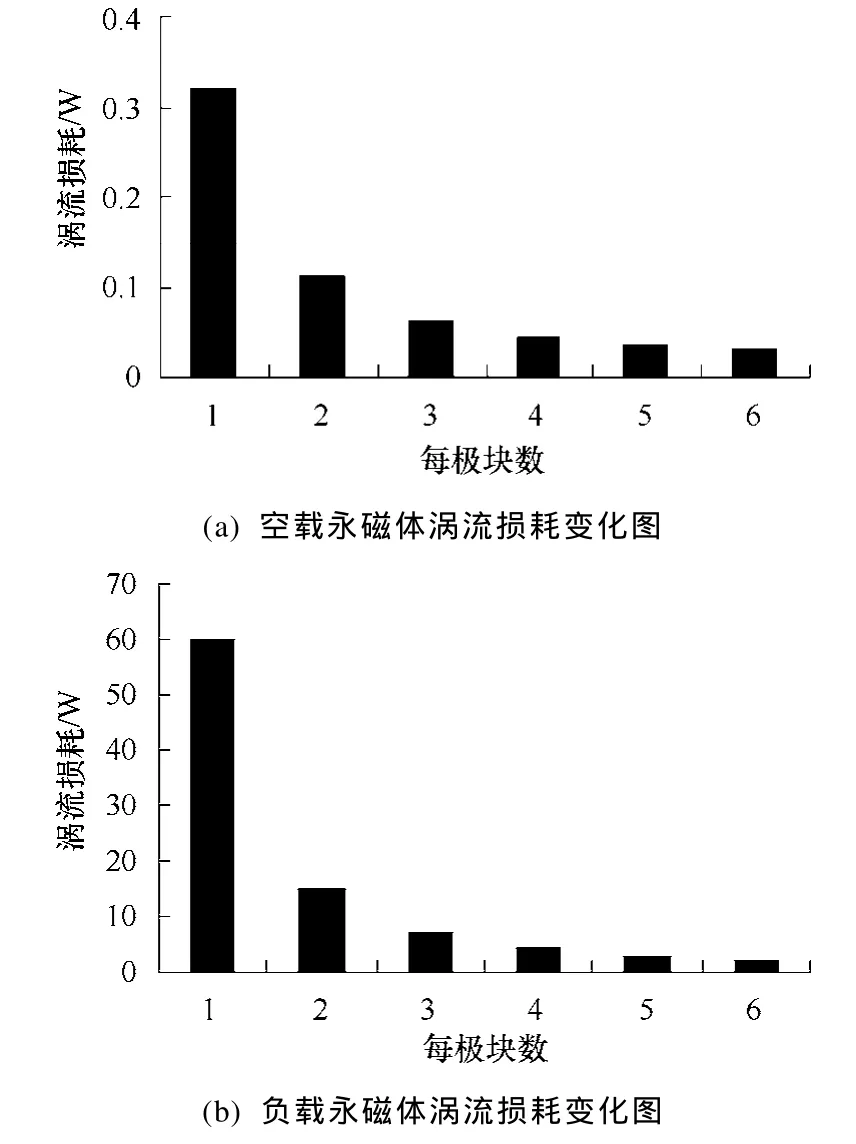
图6 永磁体涡流损耗随每极下永磁体块数变化图Fig.6 Histograms of eddy current loss in PM with the PM amount of variation each pole

4 MCM系统效率

通过对样机的涡流损耗分析，优化了两台样机的结构参数，并仿真得出了两台样机的效率Map区域，如图7所示。

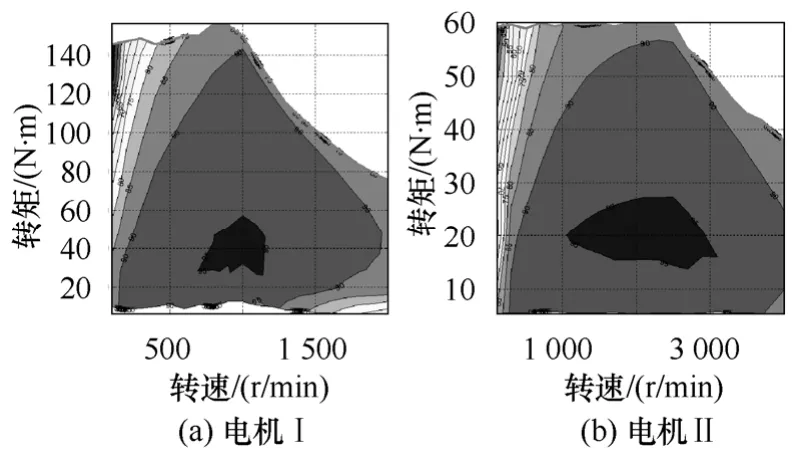
图7 单电机效率Map图Fig.7 Efficiency Map of single machine

但是，对于MCM系统来说，由于是两台电机级联系统，其效率并不只取决于单台电机，而是和每个模块电机的转矩分配策略有关。为了扩展系统高效区范围，需要采取基于转矩需求和模块电机效率Map图的具有模糊控制器的最优效率控制策略，尽可能少地使用到单模块电机的低效区来增加整个系统的高效区范围。在这个控制策略里，低效区的电机存在停机而被拖动的情况，这时就要将永磁电机的空载损耗考虑进去，系统效率Map如图8所示。

图8 MCM系统效率Map图Fig.8 Efficiency Map of MCM system

从图 8可以看出，MCM系统的转矩转速覆盖范围增加，比普通同功率电机具有更大的低速扭矩和弱磁扩速能力，效率大于90%的区域大约占全区域的 5 3.2%，效率特性得到了加强。但是对比单模块电机，特别是高速电机（电机II）在速度超过电机I的最大转速后，MCM系统效率降低，这是因为电机I被关闭，其空载损耗（特别是涡流损耗）随转速增加而增加，降低了系统效率；另外，低速电机在高速时被拖动而导致反电动势较高，对控制器耐压范围要求较高。所以，需要采取方法使电机在断电时能从系统中切除，就能解决电机被拖动造成的问题，并且增强系统容错能力，目前，可以在连接处采用单向离合器的方案满足这种要求。

5 实验研究

本文对所研制的两台样机进行了实验研究，为了验证MCM系统的效率特性，同时给出了已有的同功率样机的实验结果，并进行对比分析。实验采用被测电机与AVL测功机对拖，试验台架如图9所示。

图9 样机试验台架Fig.9 Test benches of prototypes

实验结果如图10a所示，实验结果基本与仿真结果一致。试验时限于控制器的能力，电机I过载时的峰值转矩未按照设计值进行，效率大于90%的区域大约占全区域的 50.1%，与参考样机的结果对比，可以看出，MCM 系统在低速区具有大转矩，并且效率较高，而在高速区效率较低，这是因为MCM 系统采用极数较多的分数槽电机，由于较大的铁心损耗，其单电机效率偏低（对比图 7和图10b），并且低速电机I在高速时被拖动而产生损耗，致使系统效率偏低，在设计时需要考虑解决措施。

图10 样机实验效率Map图Fig.10 The test efficiency Map of prototypes

详细的对比数据见表 3。由于 MCM系统中两台电机的端盖占用空间较大，重量也较大，造成外形尺寸增加较多，系统总重增加，功率密度较参考样机低。但采用分数槽集中绕组电机，能有效缩短电机端部尺寸，使采用自然冷却的MCM系统的转矩密度与采用水冷的参考样机转矩密度相当。

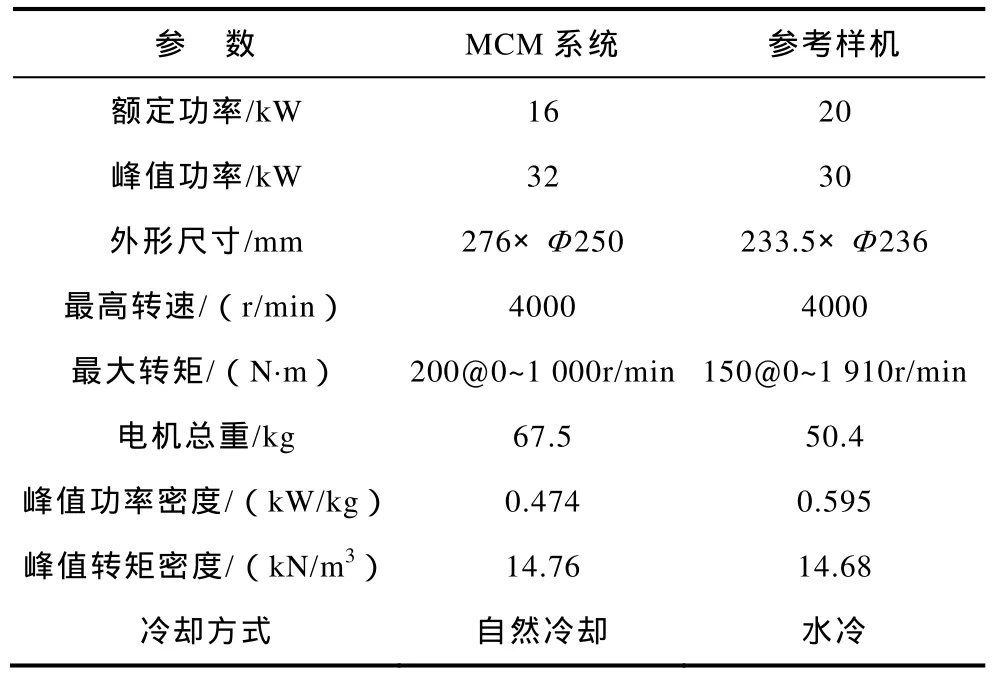
表3 样机对比结果Tab.3 The comparing results of prototypes

但是，若要提高电机的功率密度，减小外形尺寸，一是要继续减小绕组端部尺寸，二是在级联时减少端盖数量，才能和普通电机相当。

6 结论

本文主要研究了分数槽集中绕组永磁电机在MCM 系统上的应用，分析了磁动势谐波和涡流损耗计算方法，仿真了系统效率，并进行实验研究和对比验证，主要结论如下：

（1）分数槽电机磁动势谐波含量较大，会在转子上产生涡流造成损耗，特别是负载时涡流损耗较大，减小槽口尺寸能有效减小空载涡流损耗，永磁体分块能大大减小负载涡流损耗。

（2）MCM 系统具有低速大转矩和较高的弱磁扩速能力，采取有效的控制方法，可使其效率特性得到加强。但采用分数槽电机后，由于在高速区转子涡流损耗较大，系统效率降低，需要采取措施解决电机关闭后被拖动而带来的危害。

（3）MCM系统采用分数槽集中绕组永磁电机，能有效减小电机尺寸，降低电机重量，提高系统的转矩密度。

[1]韩守亮, 崔淑梅.一种新型模块化级联电机系统[J].电工技术学报,2013,28(2): 155-16 2.Han Shouliang, Cui Shumei.A new modular cascade machine system[J].Transactions of China Electrotechnical Society,2013,28(2): 155-16 2.

[2]Refaie E L A M.Fractional-slot concentratedwindings synchronous permanent magnet machines:opportunities and challenges[J].IEEE Transactions on Industrial Electronic,2010, 57(1): 107-121.

[3]Bianchi N, Bolognani S, Grezzani G.Design considerations for fractional-slot winding configurations of synchronous machines[J].IEEE Transactions on Industry Applications,2006, 42(4): 997-1006.

[4]Dorrell D G, Popescu M, Ionel D M.Unbalanced magnetic pull due to asymmetry and low-level static rotor eccentricity in fractional-slot brushless permanent-magnet motors with surface-magnet and consequent-pole rotors[J].IEEE Transactions on Magnetics,2010, 46(7): 2675-2685.

[5]Hung Vu Xuan, Lahaye D, Polinder H, et al.Influence of slot/pole number combination on performances of permanent magnet machines with concentrated windings for ship application[C].International Conference on Electrical Machines and Systems(ICEMS),2011: 1-6.

[6]谭建成.三相无刷直流电动机分数槽集中绕组槽极数组合规律研究[J].微电机,2007, 40(12): 72-77, 86.Tan Jiancheng.Investigation on slot/pole number combinations for 3-phase BLDCM with concentrated windings[J].Micromotors,2007, 40(12): 72-77, 86.

[7]陈益广, 潘玉玲, 贺鑫.永磁同步电机分数槽集中绕组磁动势[J].电工技术学报,2010,25(10): 30-36.Chen Yiguang, Pan Yuling, He Xin.Magnetomotive force in permanent magnet synchronous machine with concentrated fractional-slot winding[J].Transactions of China Electrotechnical Society,2010,25(10):30-36.

[8]彭兵, 王成元, 夏加宽, 等.磁动势法五相永磁力矩电机转矩分析[J].中国电机工程学报,2012,32(21): 105-111.Peng Bing, Wang Chengyuan, Xia Jiakuan, et al.Torque analysis of five-phase permanent magnet torque motors based on magnetic motive force[J].Proceedings of the CSEE,2012, 32(21): 105-111.

[9]Seok Hee Han, Thomas M Jahns, Zhu Z Q.Analysis of rotor core eddy-current losses in interior permanent-magnet synchronous machines[J].IEEE Transactions on Industry Applications,2010, 46(1):196-205.

[10]Deng F.Commutation-caused eddy-current losses in permanent-magnet brushless DC motors[J].IEEE Transactions on Magnetics, 1997, 33(5): 4310-4318.

[11]Yamazaki K.Torque and efficiency calculation of an interior permanent-magnet motor considering harmonic iron losses of both the stator and rotor[J].IEEE Transactions on Magnetics,2003, 39(3):1460-146 3.

[12]Yamazaki K, Kanou Y.Rotor loss analysis of interior permanent-magnet motors using combination of 2-D and 3-D finite element method[J].IEEE Transactions on Magnetics,2009, 45(3): 1772-1775.

[13]Chen Y S, Zhu Z Q, Howe D.Vibration of PM brushless machines having a fractional number of slots per pole[J].IEEE Transactions on Magnetics,2006, 42(10): 3395-3397.

[14]Toda H, Xia Z, Wang J, et al.Rotor eddy-current loss in permanent magnet brushless machines[J].IEEE Transactions on Magnetics,2004, 40(4): 2104-2106.

[15]Polinder H, Hoeijmakers M J, Scuotto M.Eddycurrent losses in the solid back-iron of PM machines for different concentrated fractional pitch windings[C].IEEE International Electric Machines & Drives Conference(IEMDC),2007: 652-657.

[16]Atallah K, Howe D.Rotor loss in permanent-magnet brushless AC machines[J].IEEE Transactions on Industry Applications,2000, 36(6): 1612-1618.