激光雷达点云数据截面提取计算方法研究

熊晓光， 王 毅

（1. 北京洛斯达科技发展有限公司，北京100120；2. 中国地质大学（武汉），武汉430074）

作为一种主动对地观测技术， 机载激光雷达(Light Detection And Ranging, LiDAR) 能够快速获取地面点三维坐标，具有全天时、全天候、高精度、成本低等特点， 对地物间缝隙具有一定的穿透性，已成为空间信息获取的主要手段之一，该技术已经在地形测绘、环境监测、三维城市建模、电力系统选线等领域得到广泛应用[1-10]. 三维可视化是近期研究热点，其关键技术之一是三维物体的截面获取与显示， 可用于显示电力线路与周边地物的空间关系，如设计线路与走廊范围内植被的高差，为设计线路及杆塔高度提供依据. 但激光雷达获取的空间三维点云具有数据量大、拓扑关系复杂、数据密度不均匀等特点，直接利用点云数据实现地物三维信息精确提取还很困难. 现有的大多数Lidar 点云处理算法在实践中用于质量控制及手工操作的时间，在整个数据处理时间中占据了较大比例[11]. 国内外一些学者开展了相关研究，点云重建方法主要为：曲面拟合[12]、分段性重建、基于物理的重建、基于神经网络的重建等[13]；其中，隐式曲面重建方法易于表示拓扑结构复杂的几何形体、无需对点云参数化，能够方便进行布尔运算[14]. 文中就如何从散乱点云数据中有效提取截面信息进行研究，通过点云数据的显示、索引、选择，基于八叉树快速生成不同方向、不同深度的断面图，能够较好展示地形、地物的空间关系，可有效应用于电力选线等工作.

1 场景管理

图1 八叉树示意图

散乱点云本身包含的结构信息较少，在进行某些操作如选择等，往往需要遍历全部点，因此这些操作的运算量会随着点的个数呈线性甚至指数级增加， 当点集的数据较大时， 交互时间会比较长.在计算机图形学中，常用场景管理技术包括加快渲染和碰撞检测等，其基本原理是通过预先计算空间物体的结构信息，并在渲染和碰撞检测时，利用结构信息排除部分数据，从而减小计算量. 常用的场景管理数据结构包括BSP 树 (Binary Space Partitioning tree)，k-d 树(k-dimensional tree), 四叉树(Quadtree)和八叉树(Octree)等. 这些树形结构的优点是，通常在判断子节点前，已通过对父节点的判断排除了大部分数据，减小计算量.

数据结构中， 四叉树通常用于处理二维数据，它的根节点为包含全部点集的四边形，在递归生成过程中， 每次将当前节点的四边形划分为上左、上右、下左、下右四等分，继续递归直到遇到终止条件为止. 常用的终止条件包括节点中点的个数小于阈值或树的深度达到某一阈值等. 八叉树是四叉树在三维空间的扩展，其每一个节点为一个平行六面体的包围盒，每次划分为八个子节点. 图1 是网格及其八叉树图像示意图，其中图1（a）为Stanford Bunny 的网格图像，图1（b）为由该网格图生成的八叉树图像. 由图1 可见，八叉树具有在原始点云稀疏的地方节点较少，在原始点云密集的部分节点较多的特性，该特性对于加速数据处理有重要意义[15].

除了生成树外，遍历也是八叉树常见的操作之一. 在点云处理中，计算当前节点包围盒中所包含的全部节点即是通过遍历实现. 取节点node 包围盒中的全部点集放入容器vec 的步骤如图2.

2 点云的快速选择

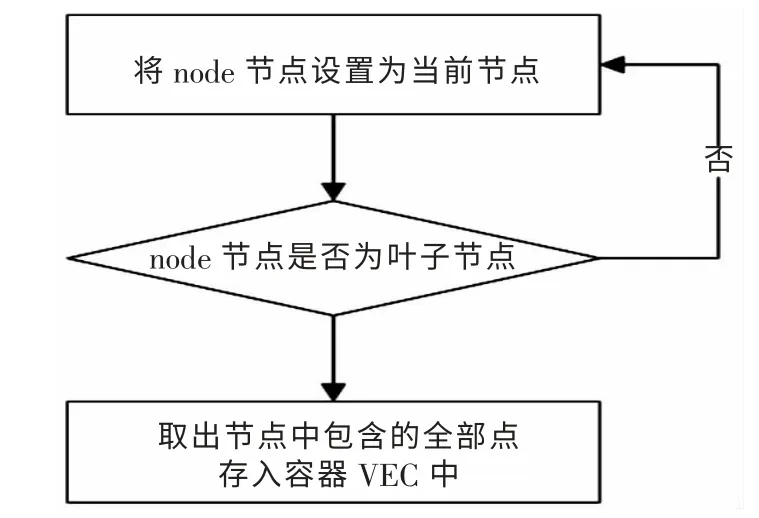
图2 递归遍历实现方式

点云的选择是常用的交互操作之一，对于某些数据， 经常需要手动选择部分感兴趣区域进行处理，或者是手动选择并删除某些噪声点. 一般使用在屏幕上画多边形的方式对点云进行框选. 为了选中多边形中的点云，需要获取当前的模型视图及投影矩阵，对当前全部点使用模型视图投影变换得到每个点对应的屏幕坐标，再计算判断该屏幕坐标是否位于多边形内部. 判断二维空间中点与多边形的关系可以通过依次判断点与多边形每条边的关系得出.

由于上述过程需要对全部点进行判断，因此随着点云个数的增加，运算速度会明显变慢. 而八叉树用于交互式选择操作的优势在于对节点进行递归调用时，可以在到达叶子节点之前排除大部分的点集. 八叉树节点的包围盒在应用模型视图变换及投影变换后得到的多边形与屏幕上用于框选的多边形有四种可能的关系，依次是：

1）包围盒投影与框选多边形相离；

2）包围盒投影与框选多边形相交；

3）包围盒投影被包含在框选多边形中；

4）框选多边形被包含在包围盒投影中.

在递归判断中，依次判断当前包围盒投影后与框选多边形的关系，如果为①，则忽略该节点及其子节点； 如果为②或④并且该节点为叶子节点，则取出其中的全部点云并依次判断与框选多边形的关系，否则继续依次判断该节点的子节点；如果为③，则调用本文上一节提到的遍历算法取出其中的全部点云，并设置为选中状态[16].

以图3 所示的四叉树及框选多边形为例，假设点集均匀分布，则在对根节点的四个子节点的判断过程中，即可排除3/4 的数据. 更特殊的情况，当框选多边形与根节点包围盒相离时，该方法仅需要判断根节点包围盒与框选多边形的投影关系， 然而，如果没有采用任何数据结构管理点云，那么将不得不对全部点云遍历一遍.

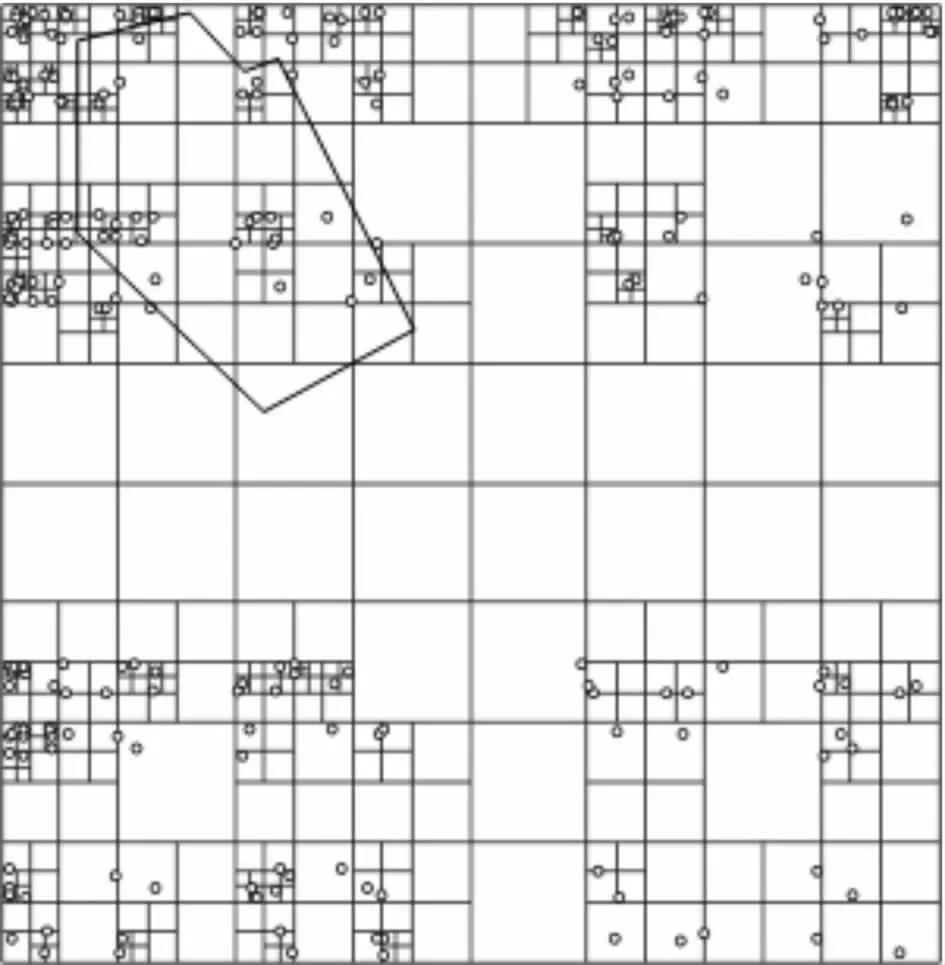
图3 四叉树中框选点云示意图

3 基于八叉树的近似横截面生成

在诸如电力布线、 铁道路线规划等应用中，经常需要获取三维地形任意方向的横截面信息. 对于机载激光雷达点云数据， 由于点云的离散特征，通常无法获取精确的截面坐标. 为了解决该问题，本文提出一种基于八叉树的替代方案，实现了近似横截面的快速生成.

前文提到， 八叉树在点云密集的部分节点较多，在点云稀疏的部分节点较少. 同时，八叉树还有另外一个特征，即点云密集的部分树的叶子深度较深，在稀疏的部分树的叶子深度较浅，即八叉树中较深的叶子节点可近似代替三维点云，如图1 所示.综合考虑上述特征，可以取八叉树中大于某一深度值的节点的包围盒与平面的交点作为点云位于该平面的近似横截面，该算法的基本过程如下[17]：

Step 1：设置节点深度阈值hmin；

Step 2：将根节点设置为当前节点；

Step 3：判断当前节点是否与给定的平面相交，如果不相交则跳至Step 4，如果相交则判断该节点是否为叶子节点，如果不为叶子节点，则依次对其子节点设置为当前节点，并返回Step 3，如果为叶子节点并且该节点的深度大于或等于hmin， 则将交点存入横截面点云，否则跳至Step 4；

Step 4：结束生成.

由上述过程可知，该算法同样基于八叉树的递归遍历， 但是由于在对节点的递归访问过程中，仅有少数的父节点与平面相交，因此可以在判断子节点之前排除大部分的父节点，从而对程序起到明显的加速作用.

任意近似断面的截取操作通过用户在2D 屏幕上画线进行交互，在获取屏幕上所画线段的屏幕坐标后，任取直线上的两点计算其视口坐标，再反投影得到这两点的三维空间坐标；同时，还可以计算出当前视线的方向向量， 该向量平行于待求的平面，将其与平面上的两点连线叉乘即可获得平面法向，从而进一步得到平面的方程. 其中，当前视线的方向向量可以通过对视口坐标（x, y, 0）与（x, y, 1）反投影得到， x 和y 可以为任意值. 三维空间中八叉树节点包围盒与平面相交的交点可以通过依次对包围盒中的边与平面计算交点得到.

4 实验结果

本节将分别介绍点云显示、基于八叉树的点云选取、点云近似横截面生成、顶点拾取和测量功能的实验结果.

激光雷达点云一次扫描得到的数据可达到数百万甚至千万，本文的可视化实验方式采用图形处理单元GPU(Graphic Process Unit)进行硬件加速，使点云显示和交互操作时控制帧率在可接受范围内， 调用OpenGL 接口和GPU 硬件驱动层上封装的C++ API，实现点云渲染和拾取等交互操作.

图4 给原始点云添加了伪彩色，伪彩色的颜色表有一定的重合， 图中黄色代表海拔较高的区域，红色代表海拔较低的区域，从图中可以看出，以海拔高度作为索引，使用颜色表对点云的颜色进行设置后，由于不同高度的点云颜色不同，因此可以较容易区分出点云的高度和边缘，从而进一步区分出建筑物和植被的形状以及地形的起伏.

图4 按高程对点云赋予伪彩结果

图5 显示了基于八叉树的任意多边形的点云选择结果，对于任意多边形，都能快速搜索到其中包含的点云，图5（a）为简单凸多边形选择，图5（b）为凹多边形选择，图5（c）为蝶形多边形选择的结果.

图5 基于八叉树的点云框选结果

图6 为使用基于八叉树的近似横截面生成结果. 图6（a）和图6（c）为从不同角度观察时横截面与原始点云叠加显示的结果， 灰色斜线为横截面，横截面的宽度为2.5m，图6（c）中的横截面与图6（a）相同. 图6（b）为从图6（a）中的同一角度观察，横截面的显示结果， 由于观察角度与横截面平行，因此横截面在图6（b）中退化为一条直线. 图6（d）为从图6（c）中同一位置观察，仅显示横截面的结果，由图6（d）可以看出，尽管这里使用的是近似算法， 得到的横截面仍然可以较好地反映地形的变化，甚至可以显示出电力塔及植被的垂直结构. 基于八叉树索引结构进行截面计算的效率与点云数量有关，当点云数量时，效率提高程度不显著；反之亦然. 在点云数量为500 万的情况下，基于八叉树索引方法计算效率提高10 倍以上.

图7 展示了基于八叉树的顶点拾取与距离测量结果. 图7（a）中电力塔的右上角红色顶点标记出了拾取的顶点，图7（b）展示了距离测量功能，量测的对象为中间铁塔两顶端间的距离， 红色顶点和蓝色线段标记出了此次测量操作，测量出的距离为11m.

5 总 结

激光雷达点云的数据处理是目前地形测绘、电力设计、数字城市等领域的研究热点，本文针对点云数据量大、结构关系复杂的特点，基于OpenGL，并通过建立三维点云的索引关系，减少了交互中的计算量，提高了点云交互的效率，适用于大量三维数据的处理. 随着GPU 的发展，越来越多的通用计算将在GPU 上完成，因此，下一步将研究如何利用GPU 进一步加速计算.

图6 基于八叉树近似横截面生成结果

图7 基于八叉树的顶点拾取与距离测量

[1] 马洪超，姚春静. 徕卡机载激光雷达的数据获取与处理[J]. 测绘通报，2008，10：70-71.

[2] 张 煜，窦延娟，张晓东. 机载激光雷达数据采集及数据处理[J].长江科学院院报，2010， 27(1)：13-21.

[3] 詹庆明，梁玉斌. 激光雷达数据处理、信息提取与应用[J]. 地理信息世界，2011，4(2)：38-39.

[4] 陈松尧， 程新文. 机载LIDAR 系统原理及应用综述[J]. 测绘工程，2007，16(1)：27-31.

[5] 王俊刚，李新科. 机载激光雷达技术在电网工程建设中的应用[J].广东电力，2009，22(9)：46-49.

[6] 周淑芳，李增元，范文义，等. 基于机载激光雷达数据的DEM 获取及应用[J]. 遥感技术与应用，2007，22(3)：356-360.

[7] 武继广. 基于机载激光雷达和遥感影像融合的地物探测方法研究[J]. 首都师范大学学报:自然科学版，2009，30(4)：6-11.

[8] 巩淑楠，陈云，徐敏. 机载雷达数据处理方法的研究与应用[J].测绘与空间地理信息，2010，33(5)：165-167.

[9] 隋立春，宋会传，马远新，等. 航空激光雷达数据处理原理及其应用前景[J]. 测绘科学技术学报，2007，24(3)：850-851.

[10] 王 蕊，李俊山，刘玲霞，等. 基于几何特征的点云配准算法[J].江西理工大学学报，2009，30(5)：768-773.

[11] 赖旭东. 机载激光雷达基础原理与应用[M]. 北京: 电子工业出版社, 2010.

[12] Hoppe H, DeRose T, Duchamp T, et al. Surface reconstruction from unorganized points[M]. ACM, 1992.

[13] Pratt V. Direct least-squares fitting of algebraic surfaces[C]//ACM SIGGRAPH Computer Graphics. ACM, 1987, 21(4): 145-152.

[14] Carcenac M,Acan A.Modeling an isosurface with a neural network[C]//Computer Graphics and Applications, 2000. Proceedings. The Eighth Pacific Conference on.IEEE,2000:165-174.

[15] Donald Hearn. 计算机图形学[M]. 蔡士杰，译. 北京：电子工业出版社，2007.

[16] Samet H. Neighbor finding in images represented by octrees[J].Computer Vision, Graphics, and Image Processing, 1989, 46(3):367-386.

[17] De Berg M, Cheong O, Van Kreveld M. Computational geometry:algorithms and applications[M]. Springer, 2008.