基于有限域中的一类逆二次特征问题设计的新HILL密码体系

严深海

（赣南师范学院数学与计算机科学学院，江西赣州341000）

0 引 言

文中研究下述有限域中的一类逆二次特征问题[1-2]及其在设计一类新HILL 密码体系方面中的应用.

问题N 对于预先给定的素数ρ 和λ，μ∈GF（p），V、W∈GF（p5×5），寻找U∈GF（p5×5），满足：

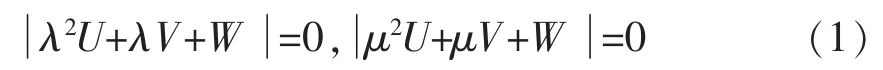
Hill 密码体系[3-4]是Lester S.Hill 1929 年提出的， 该加密算法将含有m 个字母的明文块加密成含有同等多个字母的密文块. 通过求单模数矩阵的逆A-1mod p 或求单模数线性同余方程组， 将密文解密成明文，它的提出标志着矩阵理论在密码体系设计中的应用. 游林等[5]则研究了有限域上n 元一次同余方程组的编码解法. 但HILL 密码体系也存在弱点，例如加密矩阵的存储管理问题，它不具有签名功能， 难敌通讯双方的信息伪造和抵赖，HILL 密码体系在很长时间内不被人们使用. 近年文献[6-8]研究了加密矩阵的动态构造和结合其他信息安全技术实现HILL 密码体系的签字功能. 文献[9]研究了基于多模数矩阵方程设计的密钥交换方案，文献[10]研究了基于求解多模数线性同余方程组来设计新的HILL 密码体系，文献[11]研究了基于单模数多变量二次同余方程组设计的密码体系. 文中则将逆二次特征问题[12-13]用于新HILL 密码体系的设计.

1 问题N 的解

根据U,V,W 的特殊结构，可整理得：

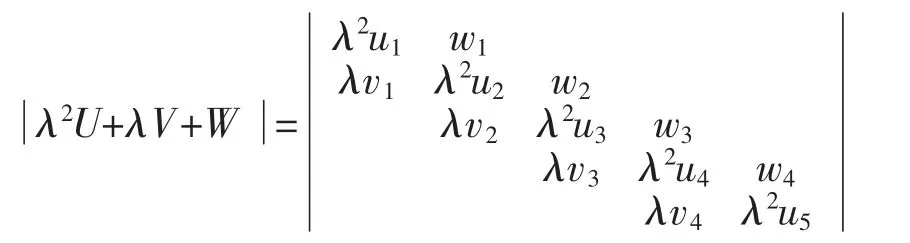
由行列式计算得：

由引理1 知问题N 中式（1）等价于φ（λ）=0，φ（μ）=0，即：

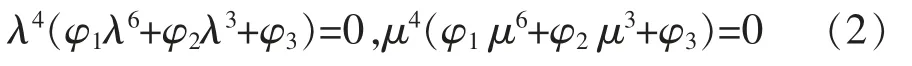
考虑到φ1，φ2，φ3的特殊结构，可整理式（2）为：

这里，γ1=v2v4w2w4，γ2=v1v4w1w4，γ3=v1v3w1w3，γ4=-v1w1，γ5=-v2w2，γ6=-v3w3，γ7=-v4w4，γ8=1.

式（3）是一个方程个数小于变量个数的非线性方程组，观察后知，该方程组可线性化为：

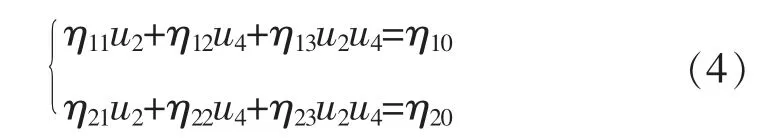
其中：η11=λ3u1（u5γ6+u3γ7），η12=λ3u5（u3γ4+u1γ5），η13=λ6u1u3u5，η21＝μ3u1（u5γ6+u3γ7），η22=μ3u5（u3γ4+u1γ5），η23=μ6u1u3u5，η20＝η10＝-（u1γ1+u3γ2+u5γ5）.

考虑到式（4）中两方程的右端相等，容易求解：

引理2 当λ≠μ，u1u3u5≠0，u2≠-（u3γ4+u1γ5）/[（λ3+μ3）u1u3]时，式（4）有解，且解的表达式为：

（1）u1，u3，u5为任意非零数.

（2）u2≠-（u3γ4+u1γ5）/（u1u3），可以任取.

（3）u4＝-u1u2（u5γ6+u3γ7）/{u5[u3γ4+u1γ5+（λ3+μ3）·u1u2u3]}

证 明：由式（4）知η20＝η10，故成立：

当λ≠μ，整理上式有：

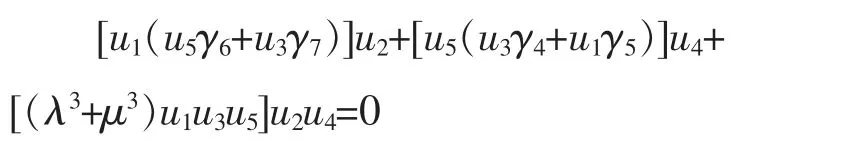
当u1u3u5≠0，u2≠-（u3γ4+u1γ5）]/（u1u3）可保证u4的表达式如下，且分母不为零：

考虑到问题N 中有限域GF（p）的要求，容易得到：

定 理 问题N 有解的条件是：

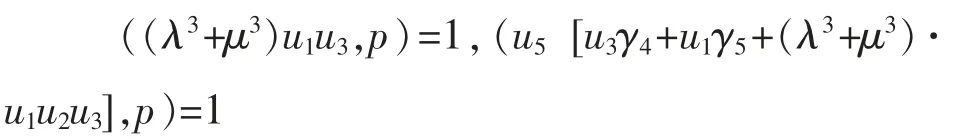
且解的表达式为：

（2）可以任取u2∈GF（p）-{ξ}，ξ＝-（u3γ4+u1γ5）·[（λ3+μ3）u1u3]-1mod p.

（3）u4≡-u1u2（u5γ6+u3γ7）{u5[u3γ4+u1γ5+（λ3+μ3）·u1u2u3]}-1mod p.

2 新HILL 密码体系的设计及算例

首先，新的HILL 密码体系（简记NEW-HILL）设计如下：

系统设置：选大素数p（通常大于216），在GF（p）中运算：

Alice：任选私钥（λ，v*）∈GF（pn），v*=（v1，v2，v3，v4），且传送给Bob.

通常n 大于100， 文中为说明算法的可行性，只取n=5，以下同理.

Bob： 任选私钥（μ，w*）∈GF（p5），w*=（w1，w2，w3，w4），且传送给Alice.

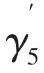
Alice和Bob：计算出γi（i=1，2，3，4，5，6，7，8），求解问题N 得u4，

构造出密钥矩阵：A=γ2U+γV+W.

Alice： 按长度为5 将明文的分组为计算出明文段mi的密文ci≡Amimod p 且传给Bob.

Bob：在GF（p）的中求密钥矩阵A 的逆矩阵A-1mod p，计算出密文段ci的明文，mi≡A-1cimod p汇总得明文m=m1，m2，…，m5.

下面，通过算例说明NEW-Hill 密码体系的可行性.

系统设置：选p=137，在GF（137）中运算

Alice：选私钥（λ，v*）∈GF（1375），且传送给Bob，其中：λ=19，v*=（v1，v2，v3，v4）＝（60，46，34，28）.

Bob：选私钥（μ，w*）∈GF（1375），且传送给Alice，其中： ,且传给组织者（见证人）.

Bob：计算

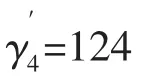
Alice和Bob：分别计算出

且求解问题N 得u4=8. 得到密钥矩阵：

Alice： 利用密钥矩阵A 加密明文m=（81，36，94，19，37）为密文:

将密文c 传给Bob.

Bob：在GF（137）中求密钥矩阵A 的逆矩阵A-1mod p，且将收到的密文c 解密为明文：

综上可知，NEW-HILL 密码体系比传统的HILL 密码体系增强以下功能：NEW-HILL 密码体系的密钥保存管理更加方便，这是因为加密矩阵是动态产生的,不是由通信双方事先选定后直接保存待用的，从而减少了密钥存储管理的困难；通信双方参与构造密钥矩阵，增强了不可抵赖性；组织者参与且见证构造密钥矩阵， 增强了不可伪造性；密钥矩阵的使用更安全，每次通信时随机求出加密矩阵，完成一次通信即可废弃这个密钥矩阵，能够实现一次一密，增强了抗攻击性；NEW-HILL 密码体系算法简练，便于固化为硬件，重复使用. 总之，文中对Hill 密码体制进行改进后得到的NEW-HILL密码体系能适应现代密码体制的需求.

[1] Lancaster P, Prells U. Inverse problems for damped vibrating systems[J].Journal of Sound and Vibration,2005，283（3）):891-914.

[2] Dong B, Matthew M Lin, Moody T Chu. Parameter reconstruction of vibration systems from partial eigeninformation [J]. Journal of Sound and Vibration, 2009，327(3): 391-401.

[3] Richard Spillman. 经典密码学与现代密码学[M]. 叶阮键，曹 英，张长富，译. 北京:清华大学出版社，2005.

[4] 杨晓元，魏立线. 计算机密码学[M]. 西安：西安交通大学出版社，2007.

[5] 游 林，王升国. 有限域上一次同余方程组的编码解法[J]. 大学数学，2008，24(4):59-63.

[6] 黄贤通，李文锋，任金威. 基于矩阵广义特征逆问题实现的具有数字签名功能的Hill 密码体制[J] . 航空计算技术，2007，37( 2) :9- 12.

[7] 任金威， 李文锋. 由RSA 实现的具有数字签名功能的Hill 密码体制[J]. 计算机安全，2007(1):38-40.

[8] 宋明明， 涂登平. 基于矩阵问题实现的具有数字签名功能的Hill 密码体制[J]. 广西民族大学学报： 自然科学版，2010，16(3):56-59.

[9] 黄贤通， 汤绍春. 基于多模数矩阵方程设计的密钥交换方案[J].赣南师范学院学报，2011(3):15-18.

[10] 林殊芳，汤绍春. 一类带有冗余信息的Hill 密码体系[J]. 江西理工大学学报，2010，31 (3):60-63.

[11] 严深海. 基于单模数多变量二次同余方程组设计的密码体系[J].江西理工大学学报，2012，33 (3):76-80.

[12] 王正盛. 阻尼弹簧一质点系统中的逆二次特征值问题[J]. 高等学校计算数学学报，2005，3(27):217-224.

[13] 吴春红. 几类矩阵的逆特征值问题[D]. 厦门：厦门大学，2009.