一类互联电力系统的部分联结稳定性分析

耿彦峰， 蹇继贵， 张炎彪

（1.忻州师范学院数学系，山西忻州034000；2.三峡大学理学院，湖北宜昌443002）

0 引 言

现代电力系统规模不断扩大，电网结构日益复杂，大容量机组逐渐增多，电力系统已经逐步形成了以大机组、超高压、长距离、大区联网为特征的复杂大系统. 电力系统的互联，可以带来显著的经济效益; 然而，电力系统的规模越大，引起系统事故的可能性也就越大. 在实际的互联电力系统中，经常会出现由于故障或其他原因引起的结构扰动，从而导致整个电力系统出现较大的结构变化. 特别是像个别子系统从互联电力系统上脱离又重新连接这样的结构扰动，它会对整个大系统的正常运行产生非常不利的影响和后果. 因此，对互联电力系统的稳定性进行分析与控制，对于提高整个电力系统的安全性和稳定性有十分重要的意义. 近些年来，很多学者对于此进行了广泛的研究，并得到了许多有意义的成果[1-4]. 但是，我们有时需要考虑的是，各子系统的部分变量对于整个大系统是否具备运行的稳定性[5-8]. 例如，假设每个电力子系统都包含一个水电机组和一个火电机组，如果只研究所有水电机组的联结稳定性，这个问题即为互联系统的部分联结稳定性. 因此，对于互联系统的部分联结稳定性研究，应该具有更广泛的意义. 但是，对于这类问题的研究仍然不是很多[9-12]. 本文在已有的理论成果上，给出一个关于互联系统的部分联结稳定性的判据. 最后，给出一个实例，并进行仿真，以说明本文结果的有效性.

1 问题的描述

考虑一类由N 个区域组成的互联电力系统，该系统包含了N 个子系统， 每个子系统分别有一个水电机组和一个火电机组，为了研究互联电力系统在不确定扰动下的联结稳定性，其数学模型可描述为：[1]

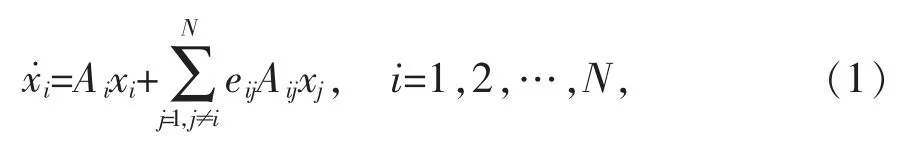
根据文献[1]，eij=1 表示第i 个子系统和第j 个子系统完全相联，eij=0 表示第i 个子系统和第j 个子系统完全分离， 用0＜eij＜1 表示第i 个子系统和第j 个子系统部分相联.

文中只考虑互联矩阵E=（eij）N×N的元素eij为0＜eij＜1 的情形下系统（1）的部分变元的联结稳定性. 那么，系统（1）相应的孤立子系统为:

下面引入互联电力系统的部分变元联结稳定性的几个相关定义.

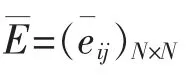
定义3 互联系统（1）的平凡解x=0 分别称为关于y 联结稳定的﹑关于y 联结渐近稳定的，若对于所有的E∈E，互联系统（1）的平凡解x=0 分别是关于y 稳定的﹑关于y 渐近稳定的.

不失一般性，为了得到有关问题的结论，我们先给出如下假设:

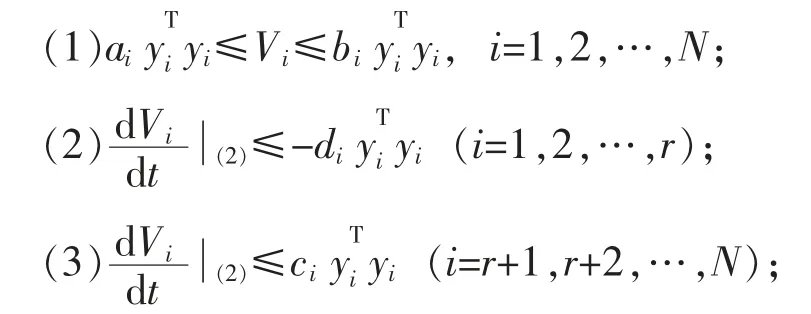
注:假设A 意味着前r 个孤立子系统的平凡解xi=0 是关于yi渐近稳定的，而r 之后的N-r 个孤立子系统的平凡解xi=0 关于yi可能是稳定的， 也可能是不稳定的.

2 主要结果

定理1 对于互联系统（1），若有以下条件成立:

（1）孤立子系统（2）满足假设A;

（2）存在一个常矩阵A=（aij）N×N，使得下式成立:

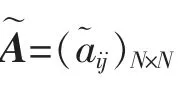
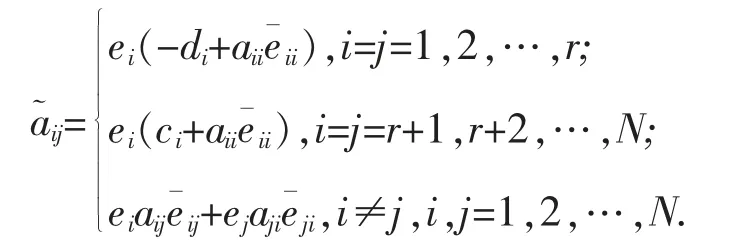
则系统（1）的平凡解x=0 是关于y 联结渐近稳定的.

证 明 对于互联系统（1）构造Lyapunov 函数:

由条件（1）可知，V 函数关于y 是正定的.那么有，

因此，对于整个互联系统有，

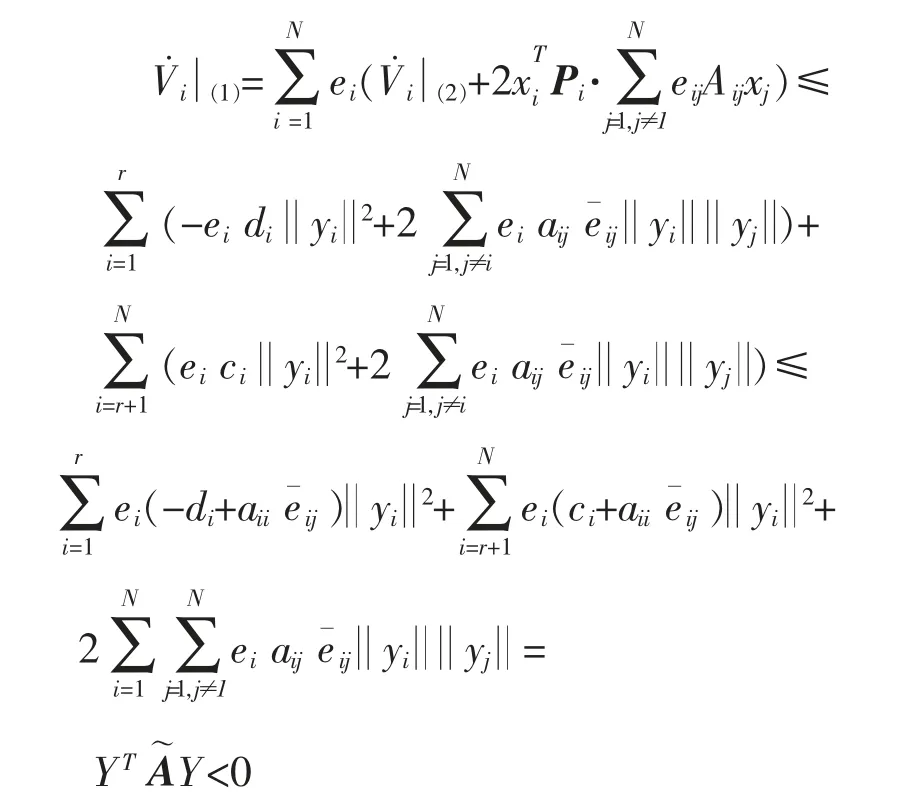
3 数值仿真

考虑具有如下形式的互联电力系统，其包含两个子系统.

其中，

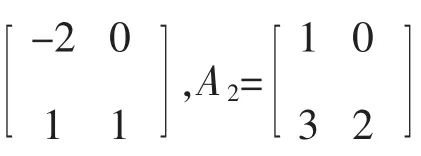
将系统（3）写成下面两个子系统:

子系统（4）、（5）的孤立子系统分别为:

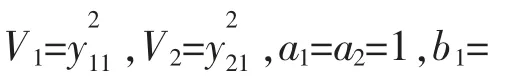
图1 部分变量y 的状态仿真

图2 部分变量z 的状态仿真

4 结 论

本文基于Lyapunov 稳定性理论以及互联大系统的关联性质，主要讨论了一类互联电力大系统的部分变元联结稳定性，建立了判别此类系统的部分变元联结渐近稳定性的充分条件.并给出一个包含两个子系统的互联系统，第一个孤立子系统是关于稳定的，而第二个是关于不稳定的，并进行了实例仿真，仿真结果说明了结论的有效性. 此外，本文的结果也可以推广到互联矩阵的元素为时变的情形，只需对条件和结论做一些相应的改变即可. 对于具有函数型的关联因子的情形，应该具有更广泛的研究意义，在以后研究工作中，仍需给予更多的关注.

[1] Siljak D D.Large-scale dynamic systems: stability and structure[M].New York: North-Holland, 1978.

[2] 谭 文，张 敏，李志攀. 分数阶互联电力系统混沌振荡及其同步控制[J]. 湖南科技大学学报:自然科学版，2011，26(2):74-78.

[3] Li X H, Wu L J. Partial robust connective stability analysis for a class of interconnected power systems [C]//Control and Decision Conference, 2008. CCDC 2008. Chinese. IEEE, 2008: 4450-4454.

[4] Ruan S G. Connective stability of discontinuous large scale systems [J]. Journal of Mathematical Analysis and Applications,1991, 160(2): 480-484.

[5] 陈宇环，易称福，张小红. 基于Lyapunov 稳定性定理的混沌同步研究与应用[J]. 江西理工大学学报，2006，27(3):34-37.

[6] 邓小飞，年晓红，潘 欢. 多个线性时滞系统的关联稳定与协调控制[J]. 控制理论与应用: 2010，27(11): 1504-1510.

[7] Nian X H, Cao L. BMI approach to the interconnected stability and cooperative control of linear systems [J]. Acta Automatic Sinica, 2008, 34(4): 438-444.

[8] 李小华，井元伟，陈雪波. 一类互联电力系统的鲁棒联结稳定性分析[J]. 控制与决策，2005，20(3): 271-279.

[9] Wang Q, Chen X B. Asymptotic equivalent analysis for LTI overlapping large- scale systems and their subsystems [J]. Lecture Notesin Computer Science, 2010(6146): 196-203.

[10] Stipanovic D M, Siljak D D. Connective stability of discontinuous interconnected systems via parameter dependent Lyapunov functions[C]//American Control Conference, 2001. Proceedings of the 2001. IEEE, 2001, 6: 4189-4196.

[11] Moreau L. Stability of multiagent systems with time-dependent communication links [J]. Automatic Control, IEEE Transactions on, 2005, 50(2): 169-182.

[12] Jian J G,Wang G H, Wang B X. Connective stability analysis for a class of interconnected power large-scale systems with respect to partial variables[J]. Complex Systems and Applications—Modeling,Control and Simulations, 2007, 14(2): 575-579.

[13] 廖晓昕. 稳定性的数学理论及应用[M]. 武汉: 华中科技大学出版社，2001.