手机“套餐”资费评价模型
吴瑞溢,侯阔林,田 敏
(黎明职业大学 公共教学部,福建 泉州 362000)
1 问题的提出
近年来,通信业务量飞涨,人们非常关心手机资费问题.手机的运营商推出了各种品牌的“套餐”,让人眼花缭乱.为此,我们希望给出合理的评价准则和方法,对各种资费方案作出评价和比较,并基于此准则为北京和上海两地的移动公司设计合理的“套餐”方案.
2 模型的假设及说明
(1)在计算手机套餐资费的时候,只考虑月基本费、本地通话及IP长途资费.
(2)以中国移动公司的各种资费标准方案为例,见下面的表1.
(3)消费者每月的通话量是稳定的,并且长期使用.

表1 中国移动手机套餐资费方案
3 手机套餐的模糊评价方法
资费方案的月基本费是多还是少,包含的主叫分钟数能否让用户满意,超出套餐部分本地主叫资费是高还是低?往往是朦胧的、笼统的和模糊的评价[1]。因此,我们评价套餐方案需要借助于模糊数学[2],通过模糊分析来给出评价结果.下面对各种资费方案提出评价准则和方法,首先确定隶属函数[3]:
3.1 月基本费的隶属函数
人们对月基本费的评价有模糊性,因为最低的月基本费为50元(依据以表1),建立如下的隶属函数:

3.2 主叫分钟数的隶属函数
在这段时间,我们对学校里的学生作了问卷调查,结果显示每人每月的本地主叫时间大多在400分钟左右,基于此建立主叫分钟数的隶属函数:
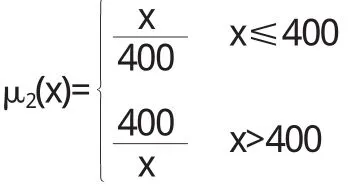
3.3 超出套餐部分本地主叫资费的隶属函数
本地主叫最低资费为0.13元/分钟,以此为依据,故
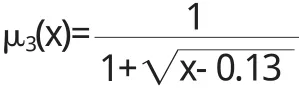
3.4 本地被叫资费的隶属函数
目前,用户认为手机应该单向收费,即本地被叫应免费服务,因此建立如下的隶属函数:

3.5 GPRS流量的隶属函数
根据我们的问卷调查,学生使用流量大多在20M左右,GPRS流量的隶属函数为:

3.6 彩信的隶属函数
根据调查结果,如下的隶属函数比较符合实际:
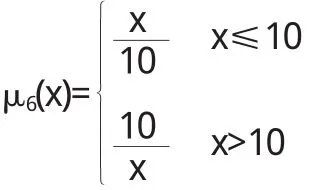
3.7 IP长途资费的隶属函数
综合分析各方案IP长途资费,得出如下的隶属函数:

根据各隶属函数计算出8个方案(见表1)所对应的不同隶属度,这样就确定了模糊关系矩阵:

权数W的取值与各因素的重要性成正比,根据调查结果,本文将规定:
W=(0.2 0.2 0.2 0.1 0.05 0.05 0.2)
把R作为模糊变换器,权数W=(0.2 0.2 0.2 0.1 0.05 0.05 0.2)表示模糊向量.
则结果为:
B=WR=(0.6656 0.6718 0.5719 0.5321 0.7238 0.5819 0.5532 0.5364)
我们将B(j)称为用户对第j种方案的模糊满意度,当然,满意度越高的方案是我们评价最高的方案.
由此可知,北京推出的“畅听99套餐”中,99元、139元和199元的方案模糊满意度均高于现行资费方案的模糊满意度,而299元的套餐模糊满意度不如现行的资费方案高。上海推出的“全球通68套餐”每一种方案的最高的模糊满意度0.7238,比现行资费标准的模糊满意度约高出35%,是目前的最佳方案。
4 资费方案最优决策模型的建立与求解
根据资费方案的模糊评价方法,本文将根据北京、上海的实际情况设计一个合理的“套餐”方案,即在不损害移动公司收益的前提下,使用户的满意度达到最高.
根据北京、上海的实际情况,我们将模糊满意度作为目标函数,把影响资费方案的主要因素作为决策变量,以移动公司的收益情况作为约束条件(不低于原方案90%),建立如下的非线性数学规划模型:
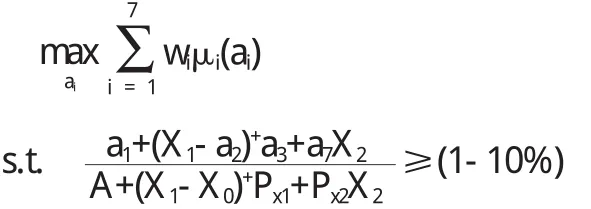
其中,μi(ai)表示ai的隶属函数,a1表示月基本费,a2表示套餐包含的主叫分钟数,a3表示超出套餐的本地主叫资费,a4表本地被叫资费,a5表示GPRS流量数,a6表示彩信数量,a7表示IP长途资费.wi表示第i个变量的权重,权重的取值与各因素的重要性成正比,根据调查结果,本文规定:
W=(w1,w2,…,w7)=(0.2 0.2 0.2 0.1 0.05 0.05 0.2)
这是一个有约束非线性规划问题,本文使用Matlab软件包[3]中的NLP求解算法.根据调查问卷取X1=400,X2=100,根据北京、上海的实际情况,取初值为
(a1,…,a7)=(139,396,0.25,0.20,10,0.1)
得到该模型的解为:
(a1,…,a7)=(136,398,0.13,0.20,10,0.05)
相应的最优值即模糊满意度为0.87476,高于原来的最佳方案(即月基本费为68元的方案其模糊满意度为0.7238).可见此模型能够给出合理的套餐方案.
〔1〕杨戍,朱瑞清.手机话费分析模型[J].洛阳师范学院学报,2004,23(02):122.
〔2〕胡宝清.模糊理论基础[M].武汉:武汉大学出版社,2004.
〔3〕赵静,但琦.数学建模与数学实验[M].北京:高等教育出版社,2003.

