基于ICA算法分离缸盖振动加速度信号的研究

李绍春，初永玲

（烟台职业学院，山东 烟台 264670）

基于ICA算法分离缸盖振动加速度信号的研究

李绍春，初永玲

（烟台职业学院，山东 烟台 264670）

本文利用基于独立成分分析的FastICA盲源分离算法对缸盖振动加速度信号进行了分离研究.分析表明缸盖振动加速度信号满足源信号独立性要求，且源信号具备非高斯特性，满足独立成分分析应用的要求.在ZH195柴油机缸盖三个不同位置安装传感器，同时测量振动加速度信号，利用FastICA算法对实测缸盖振动加速度信号进行分离.为对分离的效果进行评价，利用连续小波时频分析方法，对分离得到的活塞撞击激励的响应信号及反拖工况测得的振动加速度信号进行分析，对比结果表明，两信号的时频分布特性具有相似性，这表明FastICA算法适用于分离研究用机型缸盖振动加速度信号.

柴油机；振动加速度；盲源分离；独立成分分析

柴油机缸盖表面振动信号包含丰富的柴油机工作状态信息，利用振动信号对柴油机缸内燃烧状况进行评价具有广阔的应用前景.在柴油机缸盖上测得的加速度信号是由活塞换向撞击激励和燃烧激励等激励源混合而成的，如何能在该信号中提取与缸盖内燃烧过程相关的成分对振动信号的应用至关重要.采用盲源分离BSS（BlindS drc e Sear at a n）算法可较好的解决该问题.

本文利用基于独立成分分析的FastICA盲源分离算法对ZH 195缸盖振动加速度信号进行了分离研究.采用连续小波变换时频分析方法对分离后的信号进行了分析，对盲源分离的效果进行了验证.

1 盲源分离算法BBS数学模型

设S=[s1,s2,…是n个独立信号源，布置了n个传感器在这些信号源周围进行测量，传感器测得的信号包括直接传递和间接反射到其上面的信号，设这些信号用X=[x1,x2,…表示，分量信号xi,i=1,…,n具有相同的数据长度.传感器测得的信号与源信号间关系如下：

BBS盲源分离算法是利用传感器测量的信号X，来估计各个激励源信号S.由于这个过程中没有任何激励源信号的先验知识，而且激励源的混合过程也是未知的，因此把此类问题称为为盲源分离问题，可用图1所示的数学模型表示.

图1 盲源分离数学模型

图1虚线框中的线性混合矩阵A和源信号S都是未知的，W为研究中待求的分离矩阵，U=[u1,u2,…,un]T是最终输出结果.模型中各信号之间的关系可以表示为：

采用盲源分离目的就是能找出分离矩阵W，使输出信号U最大限度的逼近真实中的源信号S.

2 独立成分分析算法

独立成分分析（Independent Component Analysis，ICA）算法基于信号的高阶统计特性，可对混杂信号进行分离，该算法是目前应用较为广泛的盲源分离算法.采用ICA算法可找到一个线性变换，能独立统计出变换后的信号.非高斯性在中心极限定理中可作为随机信号相互依赖的度量，当其达到最大时，表示各分量信号完全独立.高斯变量在具有相同方差的随机变量中有最大的熵.对于概率密度函数为p(y)的随机变量y，其熵H定义为：

随机变量y的概率密度函数p(y)在B B S盲源分离问题中不可能得到，可以通过近似求解的方法得到负熵：

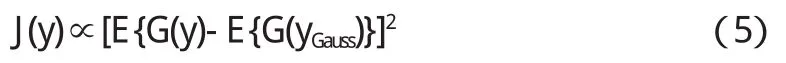
其中，E{.}为均值运算；

基于独立成分分析理论发展起来的FastICA算法是一种基于负熵的快速不动点算法.该算法的目的是通过选取W，使得J(y)最大，即E{G(y)}最大，此时：

其中g(x)是G(x)的导数，由牛顿迭代定理得：

上式等号两边同乘以E{g'(Wx)}，令W+=-E{g'(Wx)}W'可得：

由此可求出W的更新值：

通过上述迭代过程，得到一个独立分量，从混合信号中减去该独立分量，再继续重复上述过程，直至所有独立分量分离出来.

3 缸盖振动加速度信号的分离

3.1 可行性分析

缸盖上在压缩止点附近可测得的振动响应信号主要包括活塞换向撞击激励和燃烧激励响应信号.这些具有确定的时间周期和特定频率范围的响应信号满足了源信号的独立性要求.

峭度可对信号的高斯性进行度量，信号y的峭度公式如下：

公式中，u、σ分别表示信号的均值和标准差，E(x)为信号x的数学期望.kurtosis(y)>0时，信号遵循超高斯分布；kurtosis(y)=0时，信号遵循高斯分布；kurtosis(y)<0时，信号遵循亚高斯分布.利用公式计算了ZH 195柴油机8个试验工况下振动加速度信号的峭度，结果表明8个工况中峭度最小为17.36，最大为42.17.因此，研究用的柴油机缸盖振动加速度信号有超高斯分布特性.

3.2 缸盖振动加速度信号分离

在进行盲源分离时，要求测量的信号数量不少于源信号数.缸内燃烧阶段存在的激励源主要包括活塞换向撞击激励、连杆组件的撞击激励以及燃烧激励等，激励源总数可认为是3个，采用三个传感器同时测量缸盖振动加速度信号.图2是供油提前角为20°BT DC，1200 r/mi n，20 N·m工况时三个传感器测得的缸盖振动加速度信号.

图2 实测缸盖振动加速度信号

在对采样的缸盖振动信号进行中心化和白化预处理的基础上，采用独立成分分析（FastICA）算法进行分离，分离结果中仅保留了燃烧激励响应信号和活塞换向撞击激励响应信号两个主要分量，如图3所示.由图可见，分离得到的燃烧激励响应信号以低频成分为主，活塞换向撞击激励的响应信号主要为高频信号.

图3 分离得到的信号

4 分离效果验证

为了对FastICA算法分离得到的结果的有效性进行分析，测量了反拖工况，缸内无燃烧过程时的缸盖振动加速度信号，此时信号主要是由活塞换向撞击产生的，图4(a)显示了实测的缸压及缸盖振动加速度曲线.采用连续小波变换算法对测得的振动加速度信号进行时频分析，结果如图4(b)所示.从时频分析结果可以可知活塞换向撞击激励响应信号分布的频带较为宽广，其能量主要分布在5 kH z～20 kH z的高频段，在3 kH z～5 kH z间也有部分能量.

图4 反拖工况缸盖振动加速度及时频分析结果

利用连续小波变换时频分析方法对图3(b)振动加速度信号进行时频分析，结果显示在图5中.由图可见，缸内存在燃烧过程时，活塞换向撞击激励响应信号的能量仍主要分布在5 kH z～20 kH z等高频区段，而且在5 kH z附近的能量明显增强；3 kH z～5 kH z间的能量有所增加.由此可见，利用Fa st IC A算法得到的活塞换向撞击激励响应信号同反拖工况时测得信号的时频域分布特性具有相似性，时频域上能量的增加主要是由于正常燃烧工况，活塞换向撞击的能量增强所致.上述分析结果表明Fa st IC A算法可以用于分离研究用机型缸盖振动加速度信号.

图5 分离得到的活塞换向撞击激励响应信号时频分析结果

5 结论

（1）缸盖振动加速度信号的各激励源满足独立性要求，且具备超高斯分布特性，满足独立成分分析算法的要求；

（2）反拖工况测得的活塞换向撞击激励响应信号以高频成分为主，主要能量分布在5 kH z～20 kH z的高频段，在3 kH z～5 kH z间也有部分能量；

（3）利用Fa st IC A算法分离得到的活塞换向撞击激励的能量与反拖工况测得的信号具有相近的时频分布特性，表明Fa st IC A算法可以用于研究用机型信号的分离.

〔1〕A.Hyvarinen.A Fast Fixed-Point Algorithm for Independent Component Analysis[J].NeuralComputation，1997，9(7):1483-1492.

〔2〕张新成,杜志勇,周俊青.盲源分离技术及其应用[J].电声技术,2004（04）.

〔3〕A.Hyvarinen.Independent Component Analysis: Algorithms and Applications[J].Neural Networks,2000(13):.11-430.

〔4〕徐冬辉，李钊，马红光，柳冬.基于独立成分分析的雷达信号分选研究[J].信号与信息处理，2007，37（10）：17-20.

〔5〕A.Hyvarinen，J.Karhunen，E.Oja.独立成分分析 [M].北京：电子工业出版社，2007.128-129.

〔6〕纪少波.基于柴油机缸盖振动加速度信号提取缸内燃烧过程信息的研究[J].山东大学博士论文，2008（05）.

TK 421

A

1673-260X（2013）02-0018-02

山东省教育厅科技计划项目(No.J11LG87);山东省高等学校科技计划项目（NO：J10LG65）;烟台市科技规划项目基金资助(NO:2010114)